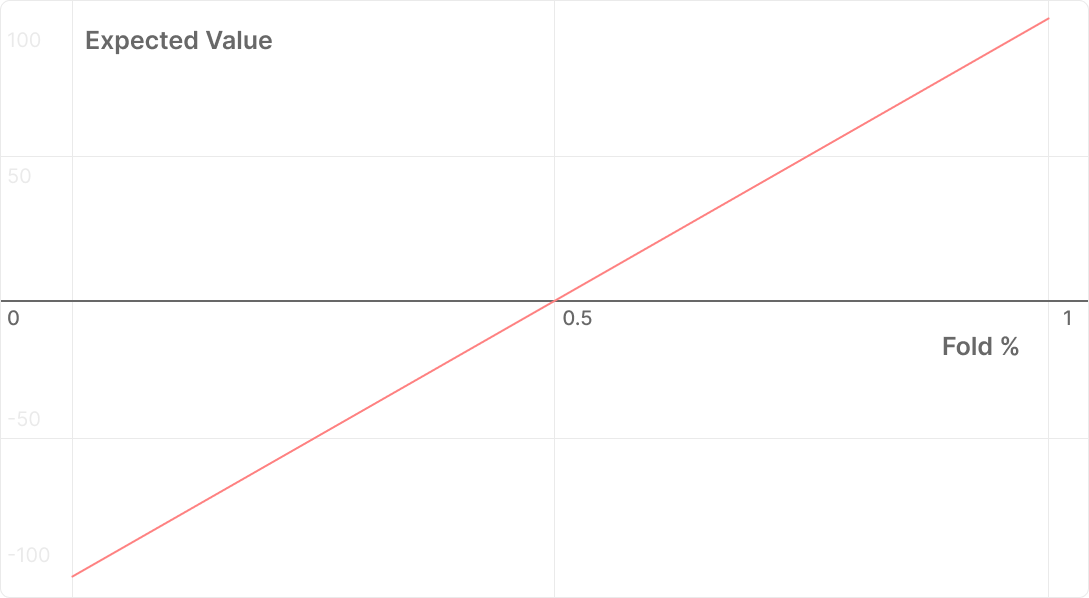MDF & Alpha
Minimum Defence Frequency and Alpha are metrics in poker that determine how wide someone needs to defend facing a certain bet size.
If you defend too wide, then your opponent can own you with value bets. If you defend too tight, then they can run you over with bluffs. So a good strategy will call just enough to make bluffs indifferent.
This metric has some problems in practice, but it’s a staple in poker theory.
What is the Minimum Defence Frequency?
Minimum Defence Frequency is a measurement that tells you how often you need to call to make your opponent’s 0% equity hands indifferent between bluffing and giving up.
MDF simply ensures that your opponent cannot profitably bluff any two cards. You need to defend the minimum frequency to prevent getting run over by bluffs.
MDF is a risk/reward calculation designed to make your opponent’s bluffs 0EV.
What counts as “Defending”?
Defending means to continue. You can defend through a raise, or through a call. Both would count towards defence.
Warning about MDF
MDF should be considered a shield to prevent your opponent from over-bluffing! First and foremost, we need to get this out of the way.
DO NOT USE MDF IF YOUR OPPONENT ISN’T BLUFFING ENOUGH.
There’s no point trying to make their bluffs 0EV if they are clearly under-bluffing. Put down your shield and embrace overfolding against value-heavy opponents. MDF should be solely used as a shield to prevent them from running you over with bluffs.

What is Alpha?
If Minimum Defence Frequency (MDF) is your shield, Alpha (α) is your sword!
Alpha is the inverse calculation. It tells you how often your opponent needs to fold for your 0% equity bluffs to at least break even.
Alpha is a risk/reward calculation designed to calculate how often your opponent would need to defend for your bluffs to break even. If you think they defend less often – great! If they defend more often, perhaps reconsider your bluffs.
Alpha = 1 – MDF
MDF = 1 – Alpha

Calculation
The Formula
This risk/reward calculation looks at the size of the bet relative to the pot to calculate the overall defending frequency needed to make bluffs indifferent.
The formula for calculating MDF/α is very straightforward.
Alpha (α) = risk/(risk+reward) where:
Risk = Amount you risk on a bluff
Reward = Amount you gain if they fold
Another formula you can use looks at bet and pot sizes. I don’t like this formula because it doesn’t work with a raise, it only works for an initial bet. But I’ll leave it here anyway for your reference.
MDF = pot / (bet+pot)
Alpha = bet / (bet + pot)
Example 1
You bet $60 into a $100 pot. Find alpha and MDF:
- Risk = $60 (You risk $60 on a bluff)
- Reward = $100 (The amount you gain if they fold)
Alpha (α) = risk/(risk+reward)
Alpha (α) = $60/($100 + $60)
Alpha (α) = 37.5%
Your opponent needs to fold at least 37.5% of the time for your bluff to break even.
MDF is simply 1 – α
MDF = 1 – 37.5% in this case, which comes out to 62.5%. So villain needs to defend at least 62.5% of their range to make your bluff break even. If they defend less often than this, your bluff would be profitable, and if they defend more often your bluff would lose money.
Example 2
You bet $60 into a $100 pot, and your opponent raises to $200. What is your MDF and their Alpha?
Your opponent has risked $200 to win a pot of ($100 + $60)
Alpha (α) = risk/(risk+reward)
Alpha (α) = $200/($200 + $160)
Alpha (α) = 55.5%
MDF = 1 – α = 44.5%
So you need to defend 44.5% of your betting range to the raise in order to prevent them from profitably bluff-raising any two cards. Conversely, they need you to fold at least 55.5% of your betting range in order to have a profitable pure bluff.
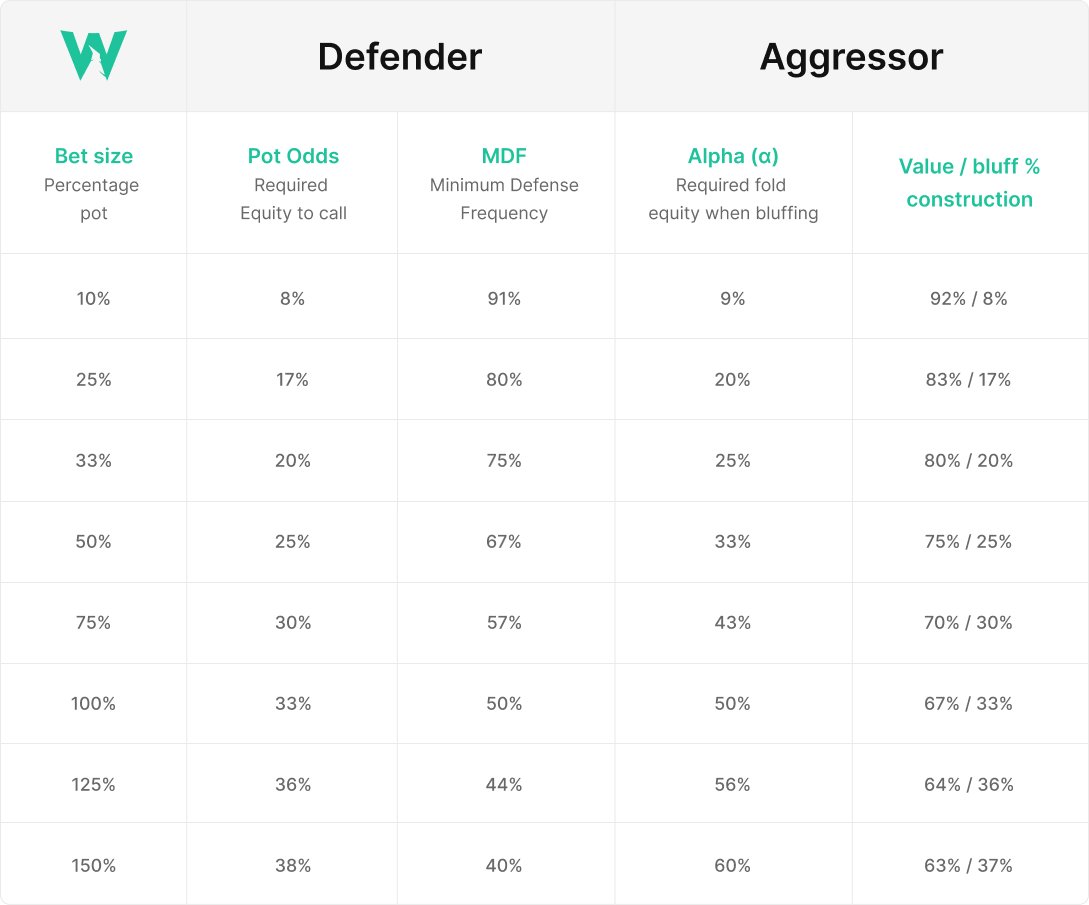
Cheat sheet
Some players simply use a cheat sheet to estimate the alpha and MDF facing a bet size. We’ve made such a cheat sheet here for your convenience! To use this chart, simply look at the bet size in the first column and find the appropriate alpha/MDF in the 3rd/4th columns.
Expected value calculations
MDF and Alpha only look for the breakeven point. We can calculate the actual profitability of a pure bluff using a simple expected value formula. This also gives us the ability to gauge a range of profitability depending on how wide they call.
The expected value of a pure bluff can be written as follows:
EV (Bluff) = (Fold% x Pot) – (Call% x Bet)
This works because the pot is how much we gain when they fold, and our bet is how much we lose when they call. For now, we’ll assume that our bluff always loses when called.
Example 3
We overbet 125% pot with a pure bluff on the river. Our opponent calls 40% of their range. We’ll say the pot is $100 for this calculation.
EV (Bluff) = (Fold% x Pot) – (Call% x Bet)
EV (Bluff) = (60% x $100) – (40% x $125) = $10
So the EV of this bluff is $10 because our opponent overfolds!
So how often would they need to fold for our bluff to be worth $0?
Alpha = risk/(risk+reward) = 125/225 = 55.5%
In other words, if they defend 44.5% of their range this overbet bluff would break even. But because they’re slightly overfolding it becomes profitable!
Graph
Let’s graph the profitability of our bluff by their folding%:
- The less they fold (left) the more money our bluff loses (down), up to a maximum of the amount we risked.
- The more they fold (right), the more profitable our bluff becomes (up), to a maximum of the pot.
Geometrically, we can draw a straight line between (0, -125) and (1, 100), and where that line crosses the x-axis represents the fold% required to break even with our bluff. This intersection is exactly alpha or 55.5% in this case.
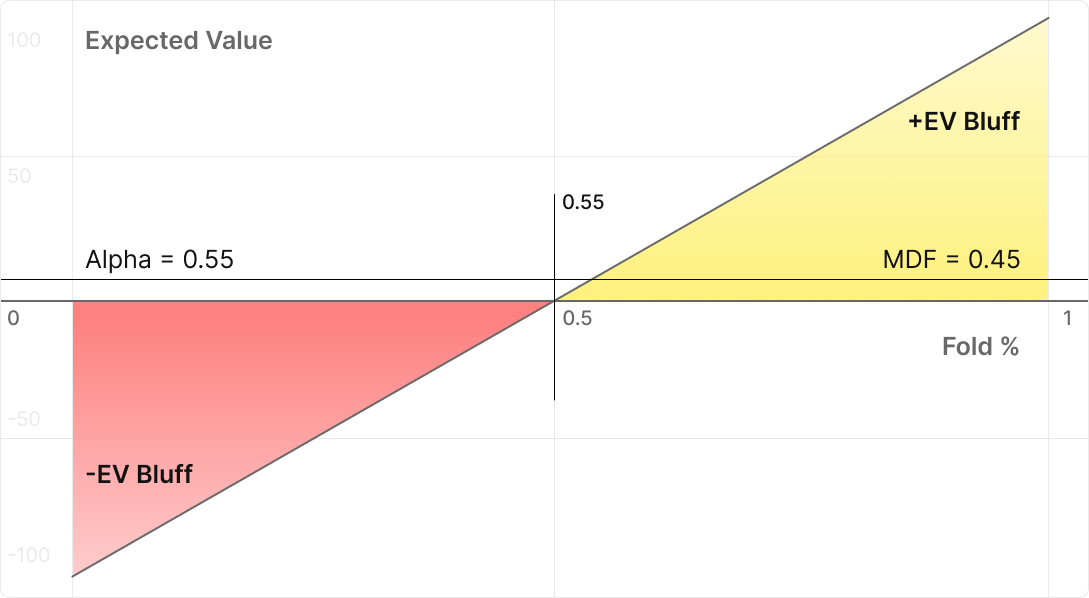
Let’s colour this graph.
On the right we can see the +EV zone, where our opponent folds more often than 55%. On the left we can see the -EV zone, where they fold less often than 55%.
Limitations
Let’s address the elephant in the room. The truth is that MDF doesn’t work well in a vacuum. MDF makes one MAJOR assumption that limits its usefulness as a standalone metric.
MDF assumes bluffs have no equity.
This does not reflect reality in most cases. In real poker bluffs usually have some equity before the river.
For example, you can semibluff with draws – even static high card hands beat some portion of your opponent’s value region.
So how does this change things?

When checking back has equity
When bluffs have equity as a checkback, you’re no longer trying to make them worth $0. Instead, your goal is to make those bluffs indifferent between betting and checking!
If your opponent is, for example, bluffing the river with made hands, you should only apply MDF to hands that can beat a bluff. It doesn’t make sense to MDF hands that aren’t bluff-catchers, since they would’ve lost to a checkback anyway.
Example
Villain shoves for pot in position on the river. Their bluffs would have 20% equity as a checkback. How wide should you defend to make their bluffs indifferent?
Your goal is to make the EV of a bluff equal to the EV of checking back. We know the EV of a checkback is 20% pot.
EV bluff = 0.2 (pot) = (fold% x pot) – (call% x bet)
0.2 = (1-call%) – call%
Call% = 40%
If this were a 0% equity bluff we’d call 50%. But, since their bluffs have value, we can overfold and only defend 40% MDF. To put it another way, we can give them a profitable bluff, because their bluffs had equity as a check.
Our goal is to make their bluffEV = checkEV
Check EV = 20% pot
Bluff EV = 20% pot (if we underdefend)
TL/DR: Underdefend when they bluff with showdown value
When bluffs retain equity against calls
Villain shoves pot on the turn. Their bluffs are exclusively draws which retain 20% equity against your calling range. The EV of checking the turn with these draws is also 20% pot. How wide should you defend to make these draws indifferent between betting and checking?
Your goal is to make the EV of a bluff equal to the EV of checking back the turn. We know the EV of a checkback is 20% pot.
EV (bluff) = EV (check) = 20% pot
We need to modify the EV equation to include their equity when called:
0.2 = (fold% * pot) + call%((win% * (bet+pot)) – (lose% * bet))
0.2 = (1 – call%) + call% (20% * 2 – 80%)
call% = 57%
A more intuitive way to interpret this is that draws risk less as a bluff (compared to a pure bluff) because they have equity when called.
A pot-sized shove with a 20% draw results in about the same risk-reward ratio as a 75% pot shove with a pure (0% equity) bluff. In that sense, it’s almost as if the bet were smaller.
This ties into why you can often bet larger on draw-heavy boards. In practice, however, you’re rarely trying to make strong draws indifferent.
Does GTO obey MDF?
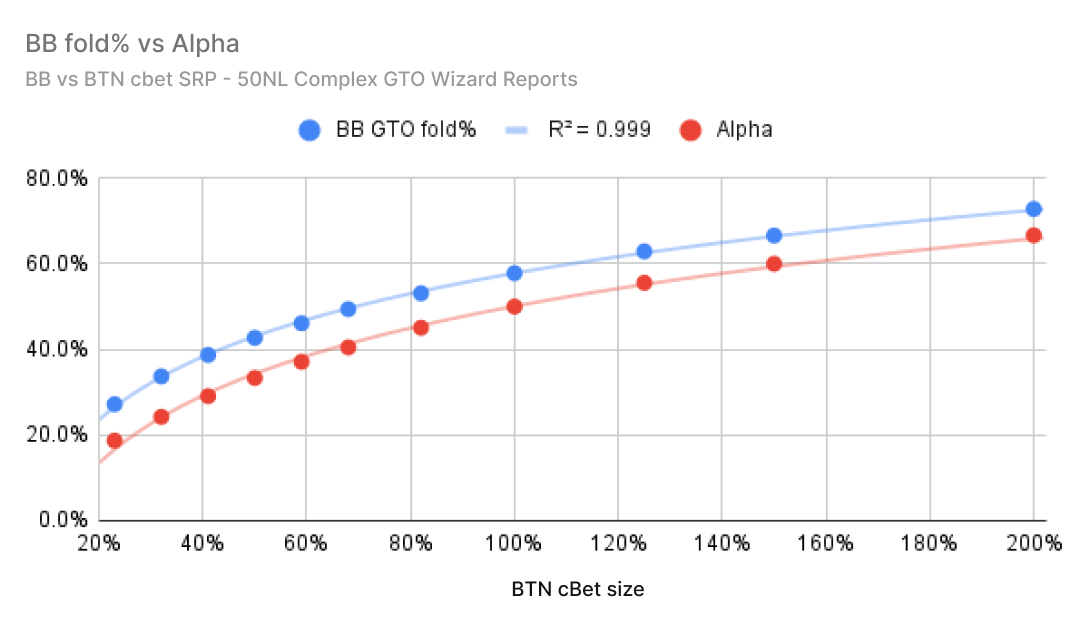
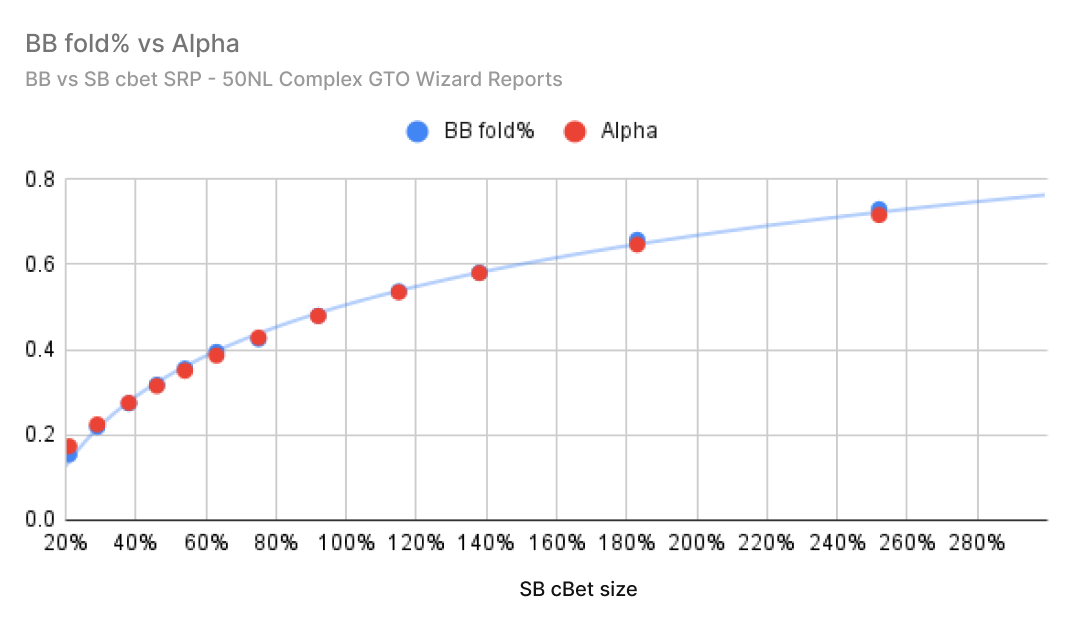
Using GTO Wizard’s complex reports, I’ve graphed the GTO folding frequency (blue) against the assumed MDF folding frequency (red). These reports encompass all 1755 strategically distinct flops. On average, BB is consistently overfolding to all bet sizes on the flop.
Here’s the same report done for SB vs BB SRP. In this case, the defender has position, and therefore calls much closer to MDF on average.
Under-defending
Underdefending relative to MDF is quite common in theory, and in fact the preferred strategy in many cases. The problem with calling according to MDF is that you take away your opponent’s incentive to bluff hands that have more than 0EV checking back.
That’s not a problem in a nuts/air toy game, but it’s a problem in real poker where bluffs have equity. Under-defending is almost certainly less exploitable than over-defending in most cases!
Generally speaking, you should defend less than MDF when:
- You’re out of position on the flop or turn (IP’s bluffs have EV when checking back)
- When villain is bluffing with made hands (Only apply MDF to hands that beat a bluff)
- When villain’s check-backs have EV
- Exploitatively, against value-heavy opponents
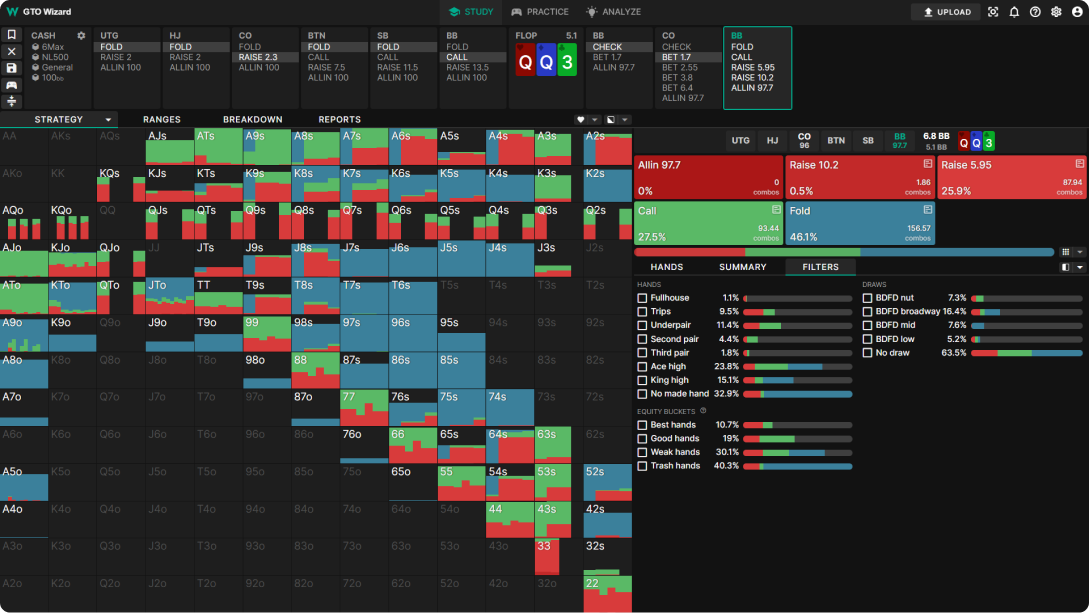
Here’s an example. This is a CO vs BB SRP on QQ3r. Most of BTN’s bluffs have significant equity and EV on this board. Furthermore, BB simply cannot realize their equity. As a result, BB needs to overfold significantly on this flop.
CO c-bets 33% pot. BB’s MDF says they defend 75% of their range, and fold, at most, 25% vs this sizing. Yet the solver is over-folding, almost half it’s range!
Over-defending
Overdefending relative to MDF is quite uncommon, but it does have its place in theory. Generally, we see over-defends in spots where the aggressor’s bluffs retain equity against the calling range. Exploitatively, you can argue for an over-defend when your opponent is over-bluffing.
Generally speaking, you should over-defend against:
- Early shoves on draw-heavy boards
- In position, when the opponent is bluffing with draws that retain equity
- On Chop boards
- Exploitatively, against bluff-heavy opponents
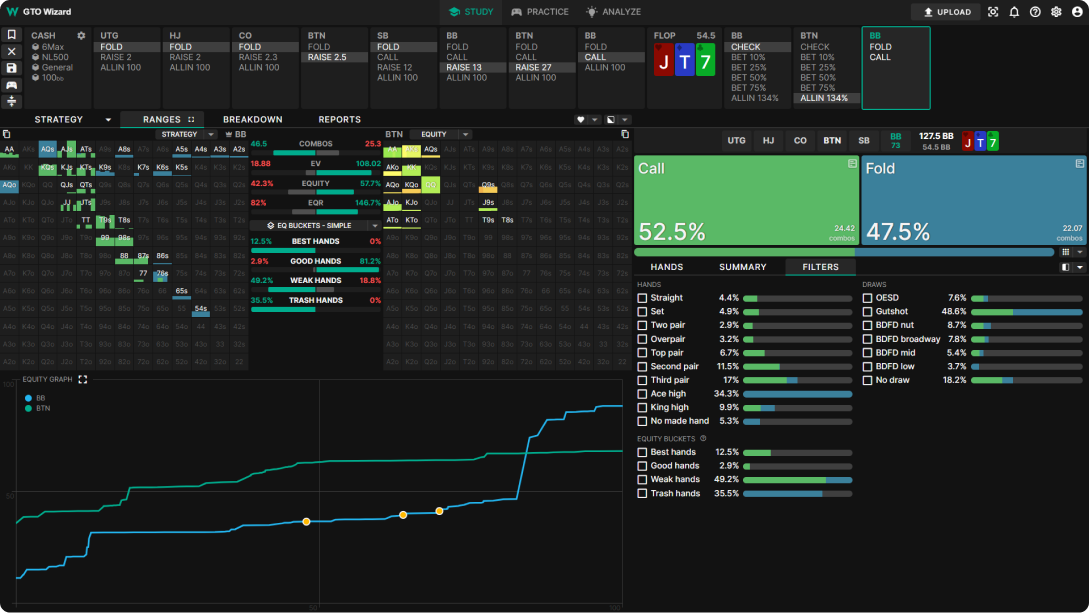
For example, here’s an interesting spot. This is a BTN vs BB 4BP where BTN shoves 134% on the flop. According to MDF, BB should fold 134/234 = 57% of their range, and call about 43% of their range. Yet the solver is overcalling by about 10%!
Conclusion
Minimum Defence Frequency is a shield used to prevent your opponent from running you over with bluffs. Alpha is a sword used to determine how often you need them to fold to justify risking a bluff for some bet size.
This metric is not perfect, as it assumes bluffs have no value. However, it is a useful guide to determine roughly how wide to defend, or roughly how often you need to see a fold. You should exploitatively adjust if you think your opponent is over or under-bluffing. Do not rely on MDF as a crutch.
GTO strategies closely follow MDF in position and consistently overfold out of position. (on average).
This metric obviously has value and can be applied in many more ways than we’ve shown in this article. For example, you can use it to determine approximate value thresholds of different lines.
Hopefully, now you have a better understanding of the theoretical and applied application of Alpha and the Minimum Defence Frequency!
Author
Tombos21
Tom is a long time poker theory enthusiast, GTO Wizard coach and YouTuber, and author of the Daily Dose of GTO.