Do Multiple Sizes Matter?
Should I work out the other tools or just stick to the crowbar?
Solver results can appear daunting when they employ many different bet sizes at a single node, especially if most hands mix across all sizes with no clear heuristic for choosing between them. There are methods for making sense of the apparent madness, but it also helps to understand what this mixing is worth and when you might be better off with a simpler strategy. Let’s find out together!
Continuation Betting
Flop solutions tend to be the most complicated because the solver is balancing its strategy for tens of thousands of possible turn and river scenarios. When it uses multiple bet sizes, each betting range must be robust, not just on the current street but in all these future scenarios as well.
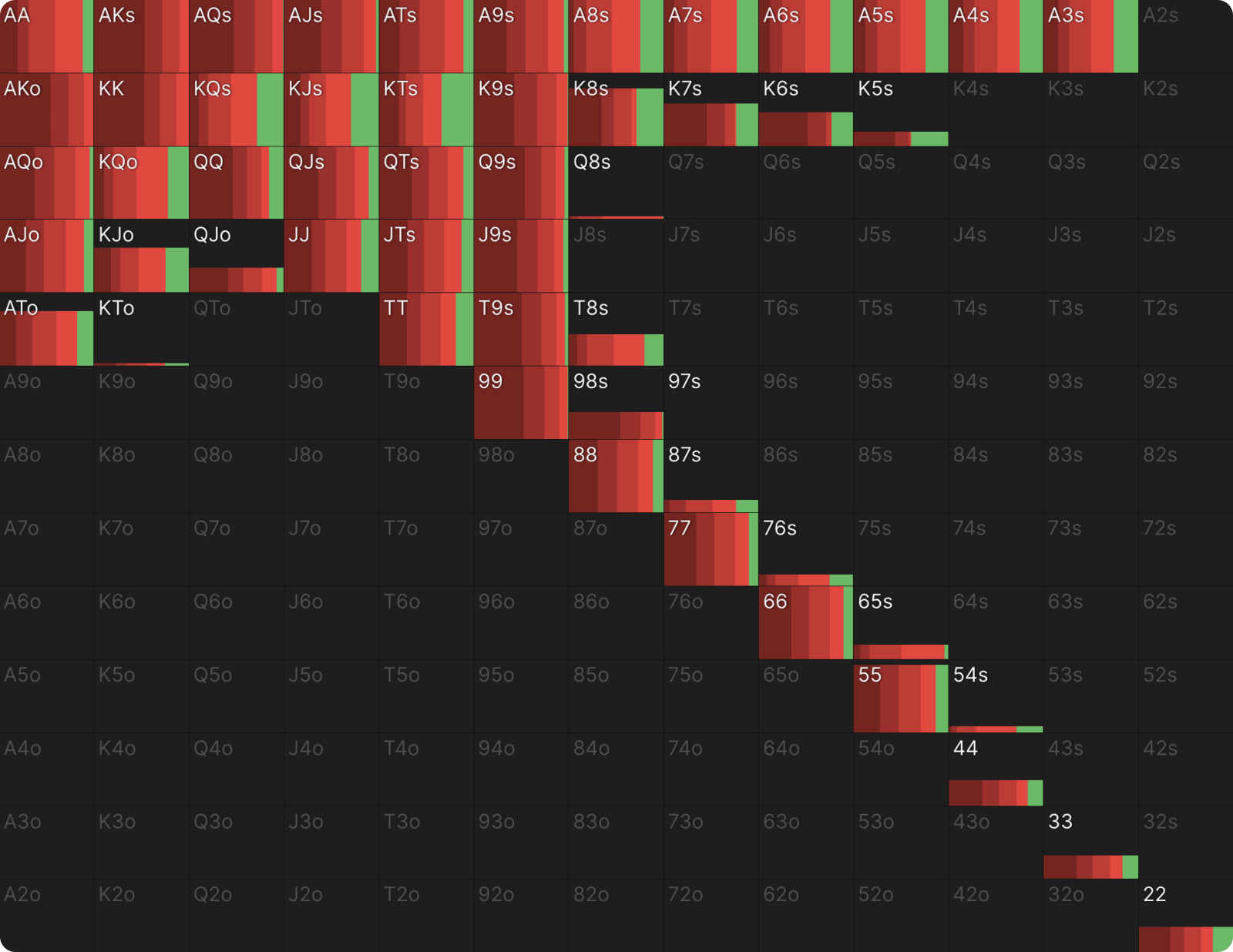
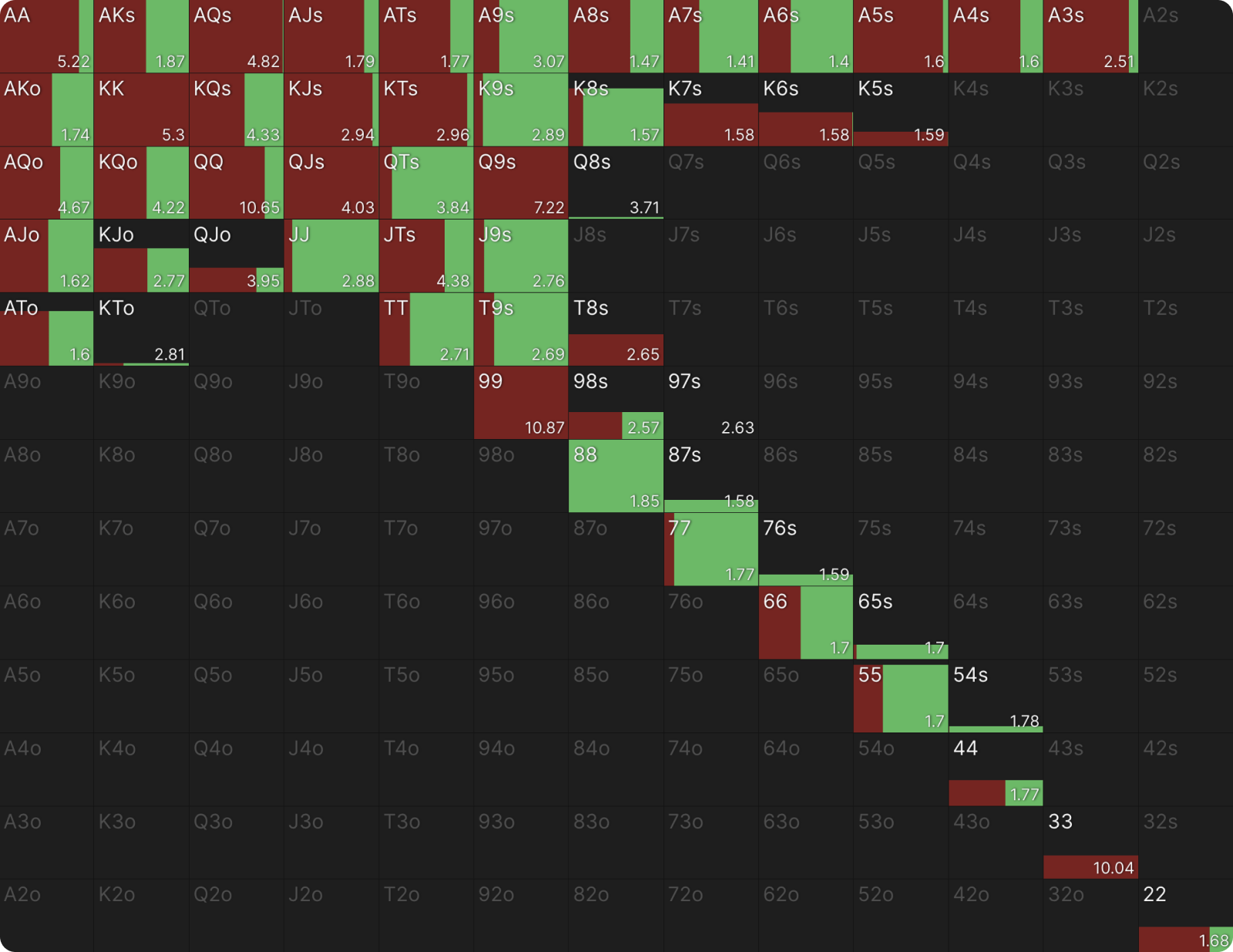
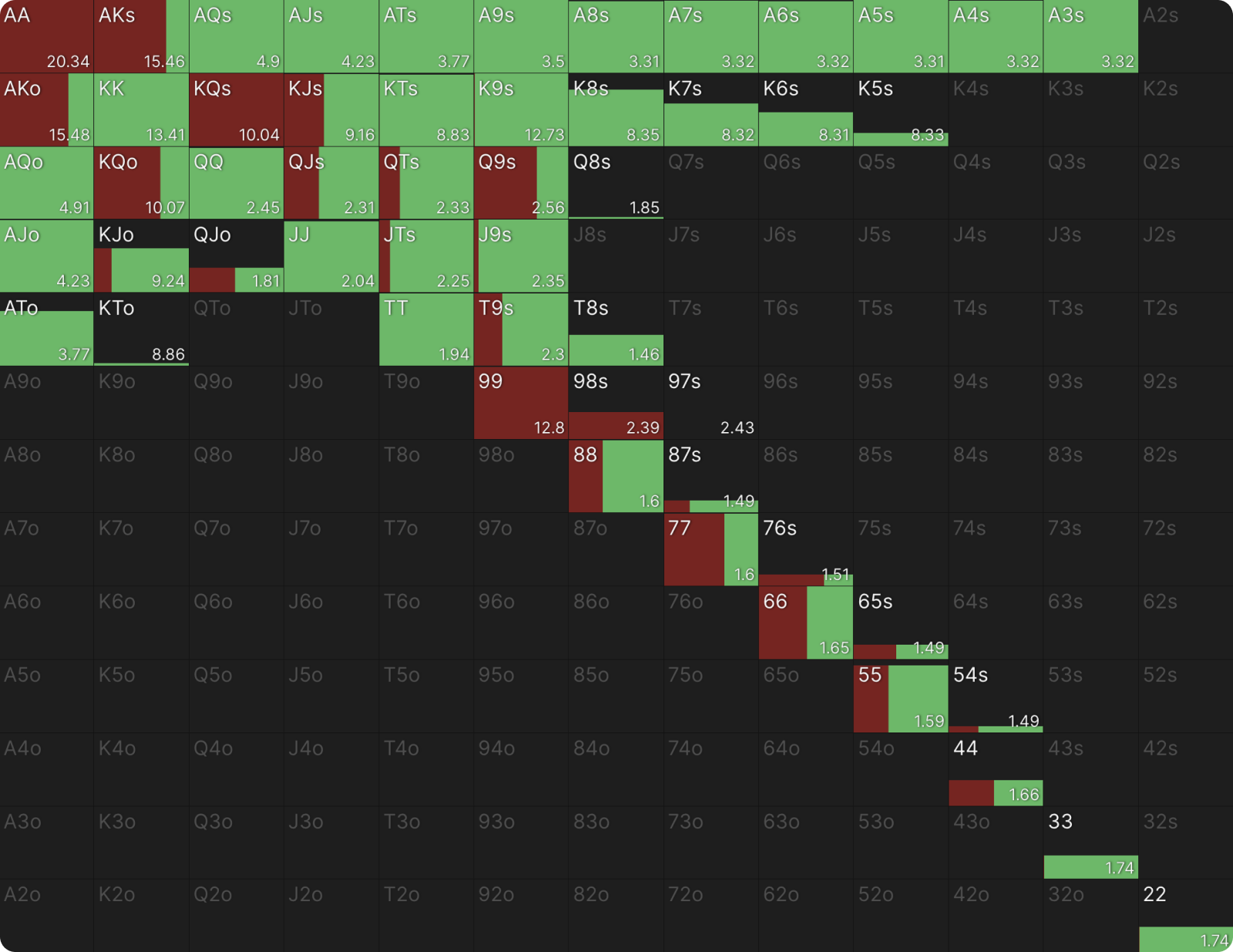
For a computer, this is a tractable problem. It can crunch the numbers and spit out something that looks like this:
That’s five different ranges, with none clearly dominant over the others and most hands mixing across all of them. There are some trends drowned by the noise; hand classes that skew toward one size or another, but mixing is essential to prevent exploitation. There are, for example, just enough strong hands in the small bet ranges to keep BB indifferent to check-raising more aggressively. That’s the kind of precise balancing a computer can execute, but a human cannot.
Experiment Setup
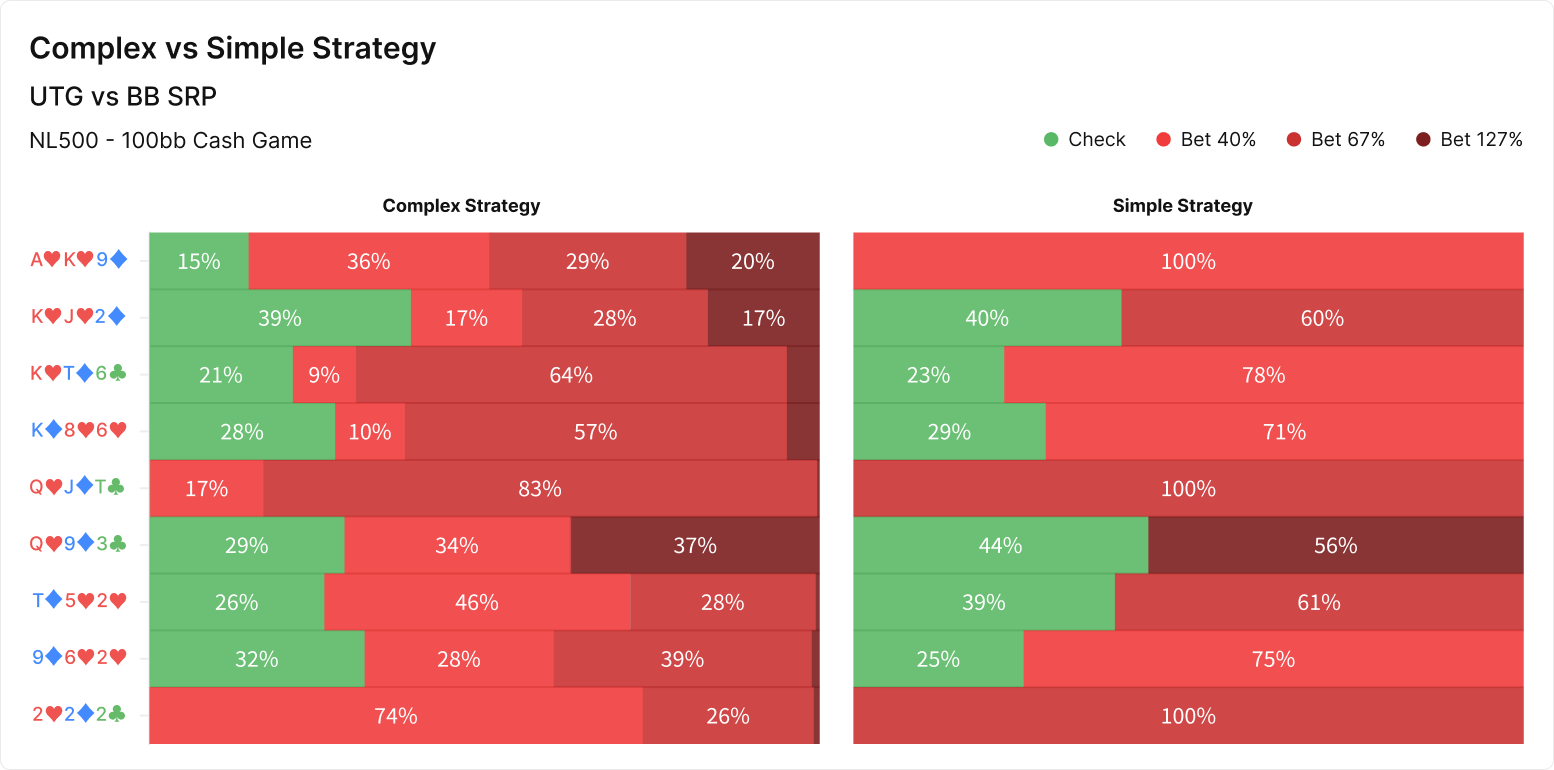
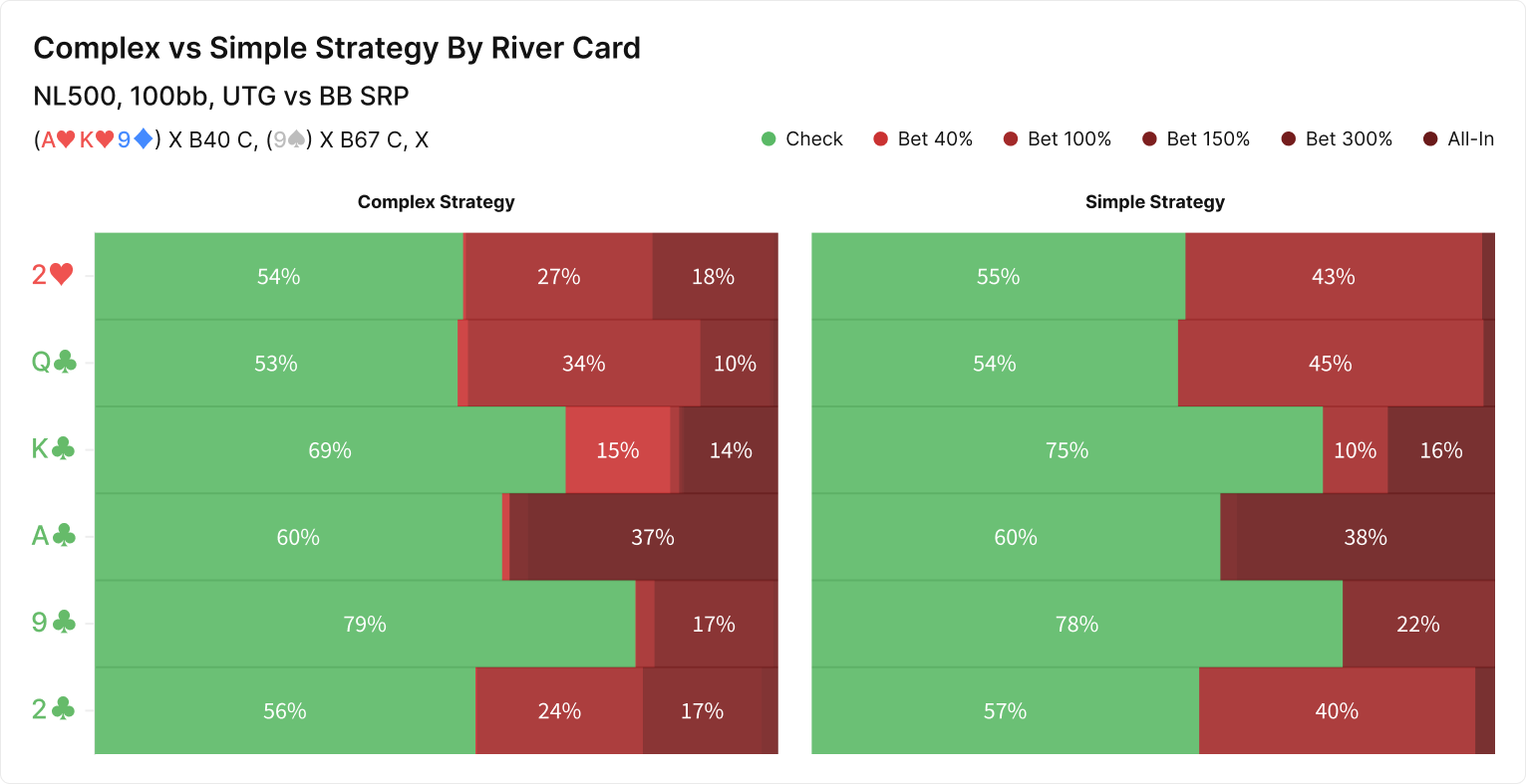
To see what all this complexity is worth, we will examine an assortment of flops with complex continuation betting strategies in the UTG vs BB formation in a 100bb cash game single-raised pot (SRP). The horizontal bar chart on the left of the first graphic represents the complex strategy, a Fixed simulation where UTG may bet 40%, 67%, or 127% of the pot, and all other bets and raises are determined with the Automatic feature. Because UTG’s flop bet size options are fixed, their raise size must also be fixed; I chose 50%.
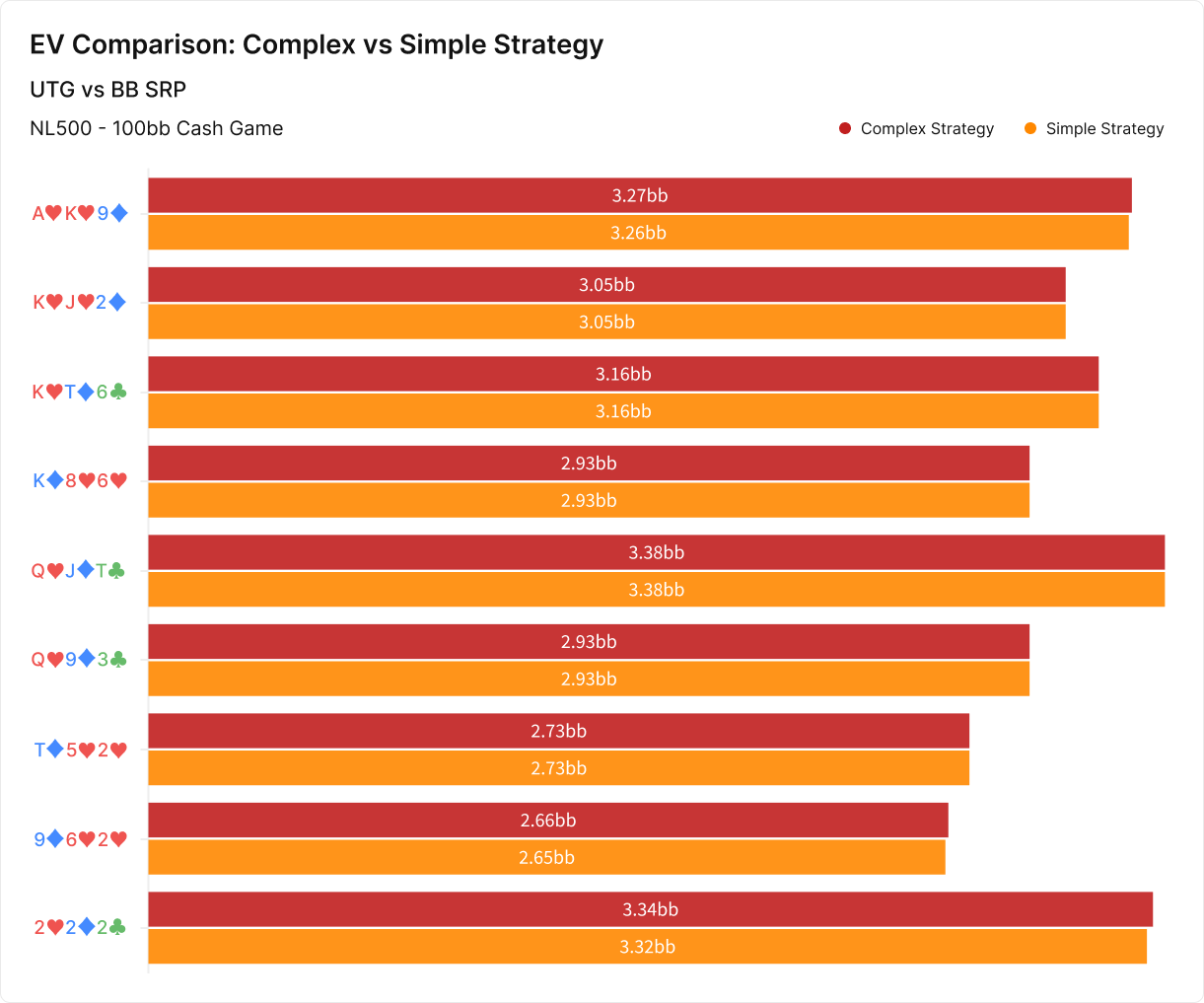
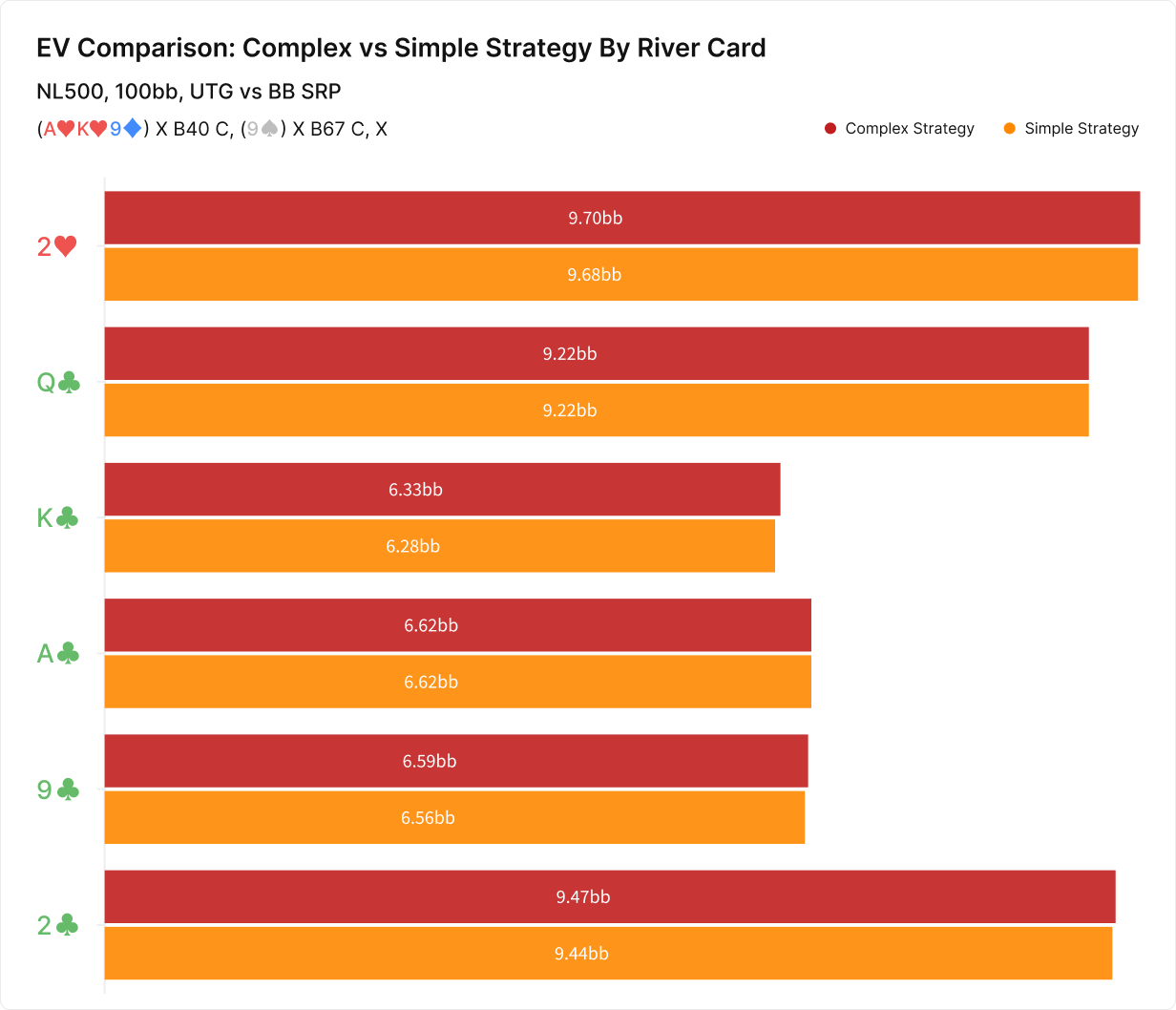
The horizontal bar chart on the right of the first graphic represents a simulation where all bet sizes, including the continuation bet, are determined with the Automatic feature. This means the solver is restricted to a single bet size but may choose whichever size offers the highest EV. The EVs for each complex-simple strategy couple per board are shown in the second graphic.
On most of these flops, the EVs of the two strategies are within one one-hundredth of a big blind of each other. In the worst-case scenario, the simple strategy loses .02bb relative to the complex one.
Two-hundredths of a big blind is less than .5% of the pot, but it isn’t trivial. That’s 2bb/100 hands, a substantial portion of anyone’s win rate. If you could actually claim that 2bb/100, it would be well worth pursuing.
Chasing small edges risks greater exploitability if you implement a complex strategy imperfectly.
The risk is that, in trying to chase that small edge, you introduce a lot more exploitability into your game due to inaccuracies in the implementation of the complex strategy. For example, the strategy shown above for the A♥K♥9♦ flop entails a lot of mixing the same hand across different bet sizes to keep the opponent indifferent between a variety of counterstrategies. If you tried to use these different sizes with a simple heuristic like “bet bigger with a more polar range and smaller with thin value bets and semi-bluffs,” a savvy opponent could exploit this by aggressively check-raising your smaller bets while never raising the bigger ones. This exploit would cost you much more than the .01bb difference between the equilibrium EV of the simple strategy versus the complex one.
Wait, There’s a Catch!
On some of these flops, the simple and complex strategies end up playing many hands the same way. This could be because the flop incentivizes a fair bit of checking or because a single bet size predominates even in the complex strategy, with many other hands preferring a size that’s only slightly different (67% vs 40% pot, for instance).
In cases where a complex strategy employs dramatically different bet sizes, the simple strategy may actually lose significant EV with the hands that would have preferred a much different size. The loss of that option may not affect the overall EV of the spot because those hands are a small part of UTG’s range, but this would mean when dealt those specific hands, UTG would be losing that EV by playing the simple strategy.
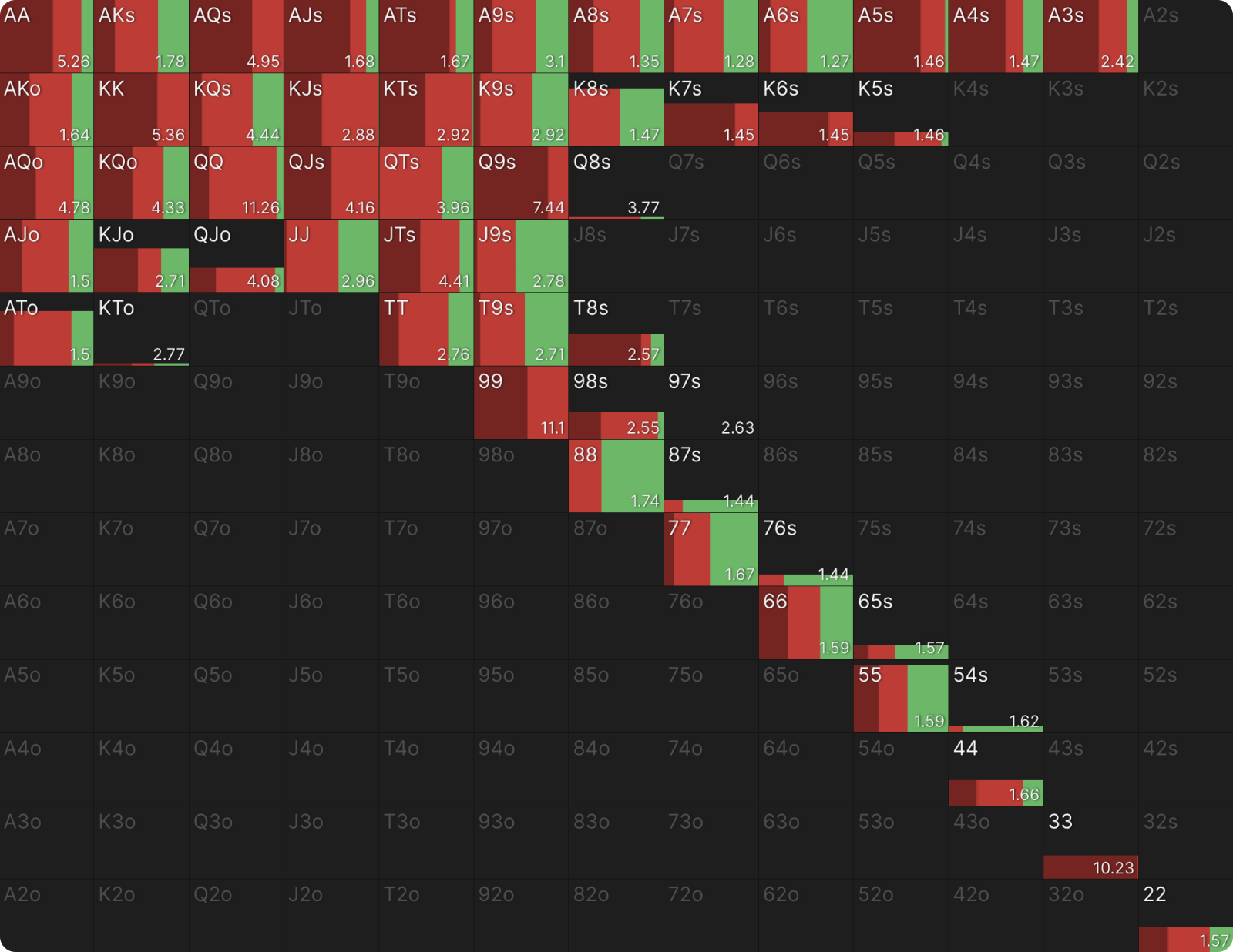
The best example of this is the Q♥9♦3♣ flop, where the complex strategy mixes between betting 40% pot, betting 127% pot, and checking. To employ the simple strategy, which loses the 40% pot option, UTG must compromise by taking a subpar line with the 33.6% of hands that would have preferred the small bet. These hands (like JJ, T9s, and QTs) which could have bet small for thin value and protection but are not strong enough to build a large pot with an overbet (nor weak enough to benefit from the folds such a bet would garner).
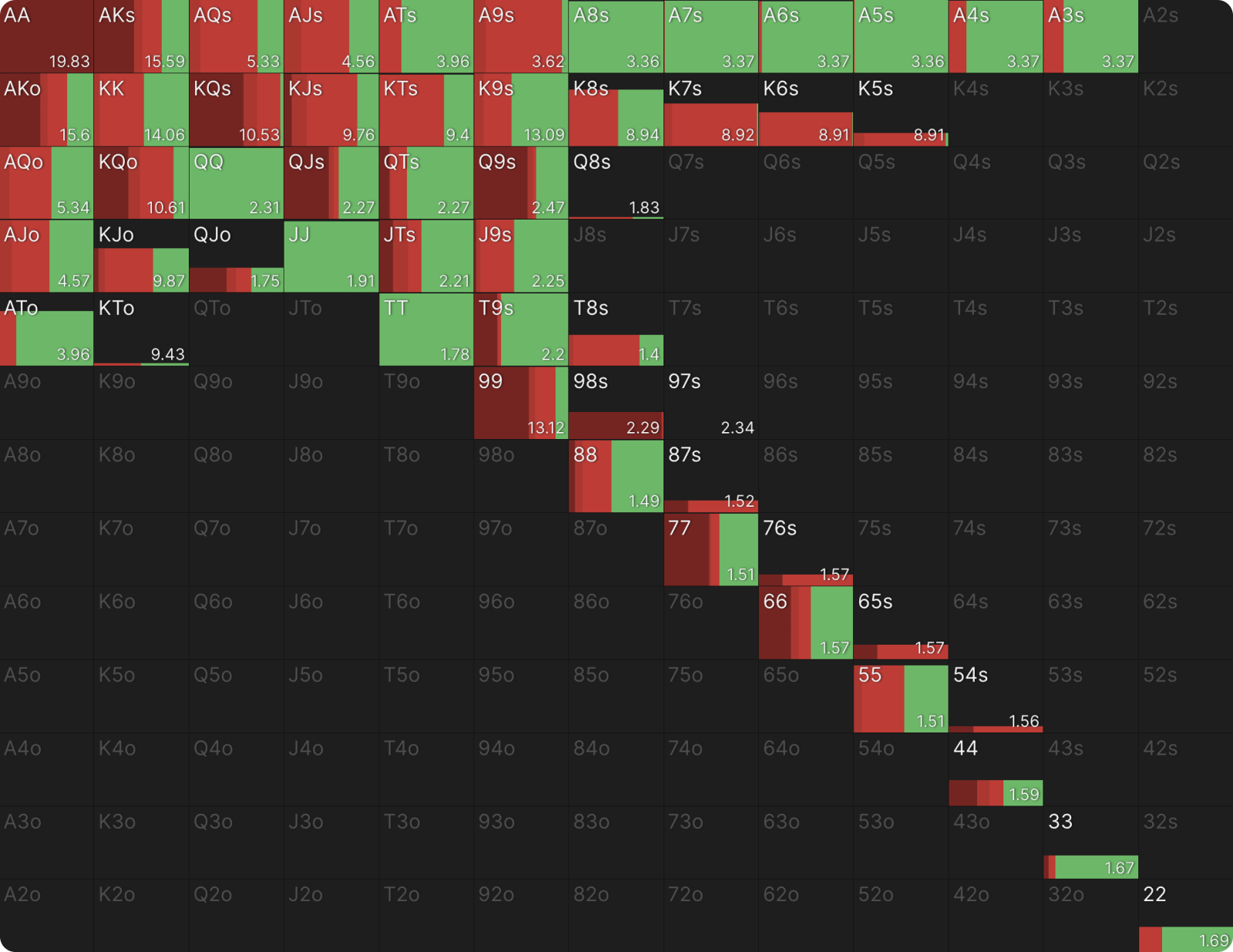
If you compare the EVs in the chart above to those for hands in the simple strategy (shown below), you can see that these hands do in fact lose value by foregoing the opportunity to bet 40% pot. QTs, for instance, is worth 3.96bb in the complex strategy but only 3.84bb in the simple strategy.
However, this is offset by many other hands gaining value in the simple strategy. KJs, for instance, is worth 2.94bb in the simple strategy versus 2.88bb in the complex strategy.
UTG’s (simple) checking range is stronger because it includes some hands that would have bet 40% pot if given the opportunity (like in the complex strategy). This decreases the value of those hands but increases the value of other hands in the checking range, including some 88 and 77, that would have mixed check or bet small on the flop.
In the end, these mostly balance each other out, though we should expect the simple strategy to slightly underperform the complex one when played by a solver. The loss is not large because the hands that miss out on betting small on the flop can make up the difference later. Because these hands would mostly check back the turn after betting the flop, they can instead check the flop and bet the turn and accomplish much of what the ‘bet flop and check turn’ line would have accomplished.
Barreling the Turn
The flop is more forgiving of simplification because there is room to make up the difference later. If you bet small with a hand that wants to play a large pot, you can still bet big—even overbet—the turn and river and ultimately put in just as much money as you would with the line that starts with a larger flop bet. Likewise, if you make a large c-bet with a hand that will not perform well in a large pot, you can check back the turn and still arrive at the river with an appropriately-sized pot. As you get closer to the river, there is less room to “make up the difference” in this way, so it becomes more important to follow the incentives of your hand even when that entails a more complex strategy.
The closer to the river, the less room to make up the difference later after a suboptimal bet size.
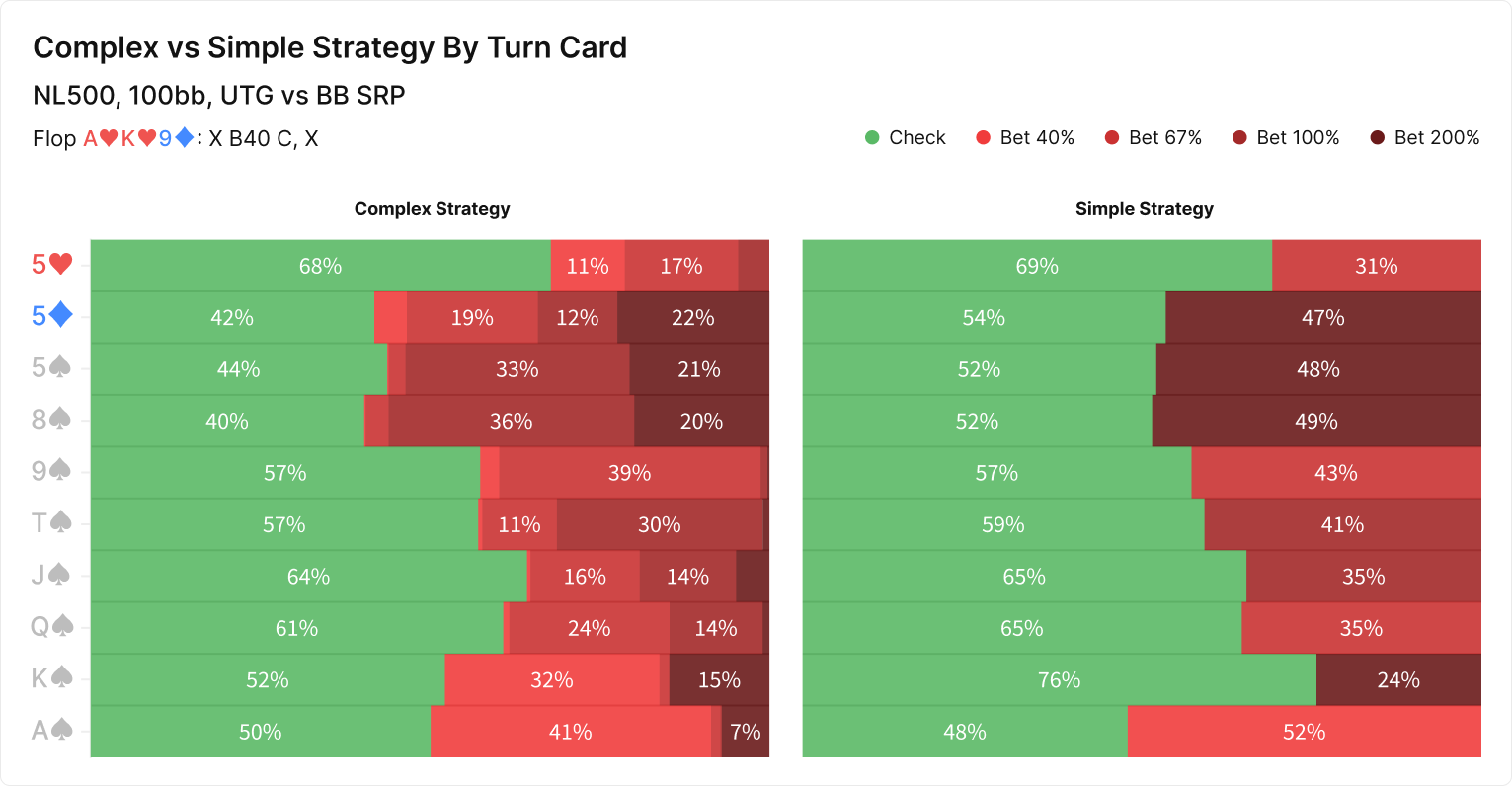
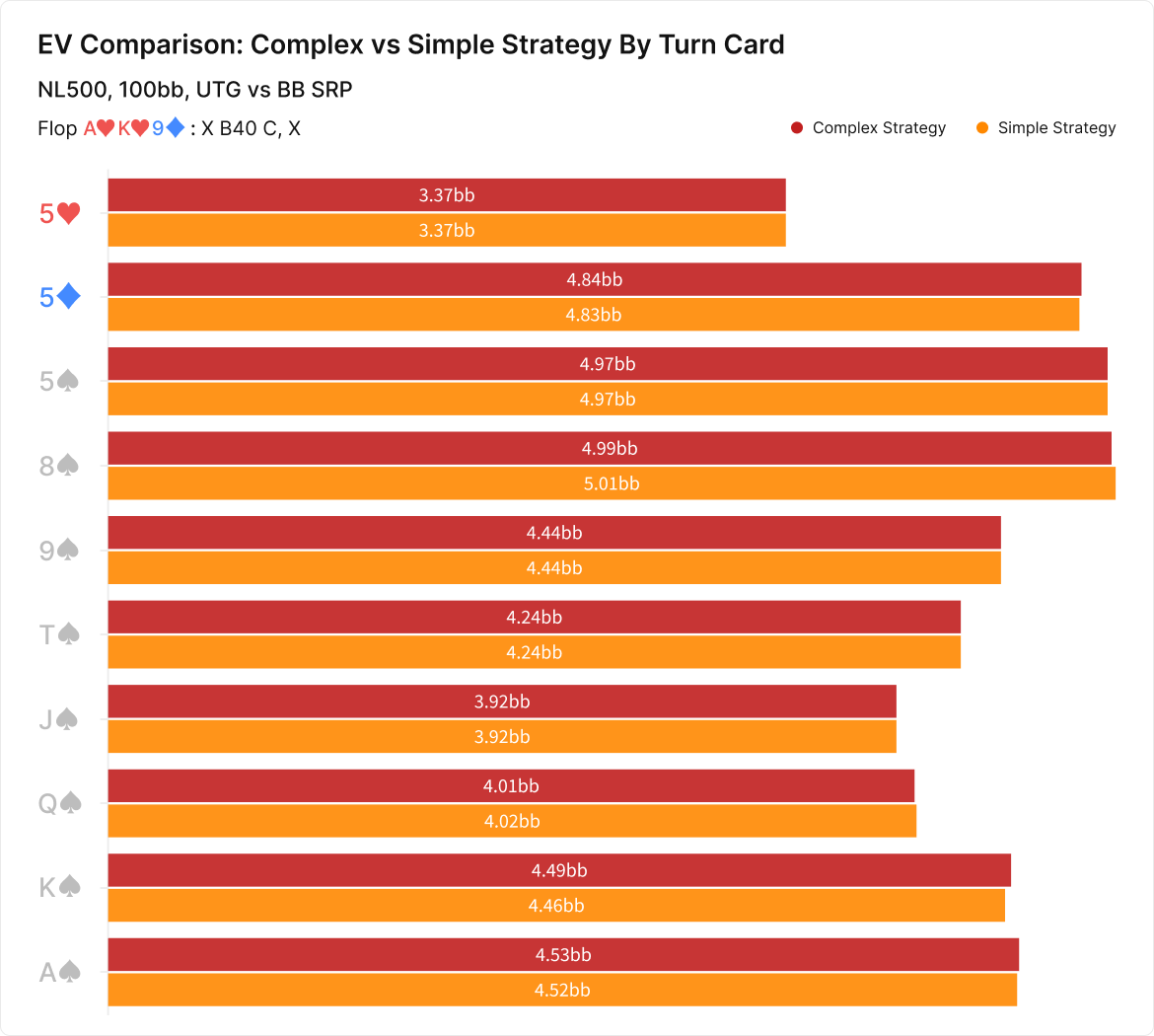
Even so, the difference is not dramatic. The following chart shows UTG’s strategy for barreling various turn cards after BB check-calls a 40% pot continuation bet on A♥K♥9♦. The left side shows the complex strategy, where the solver can mix four different bet sizes, and the right shows a simple one where it chooses a single bet size automatically. The corresponding EVs of the strategies are displayed in the second graphic.
8♠ Turn
The differences in EV appear comparable to the flop. There are even some cases where the simple strategy appears to have a higher EV, though that’s merely a result of the solver’s margin of error. If purely betting 200% pot on an 8♠ turn were actually more profitable than mixing between 100% and 200% pot, the solver would choose the simpler strategy even when given the option of playing the more complex one.
What’s actually happening here is that the simple and complex strategies take the same actions with the same hands more often than on the flop. Both strategies check at least half the time on most boards, a much higher checking frequency than on any of the flops we looked at. In those cases, the simple strategy isn’t sacrificing anything because it’s taking the same action the complex strategy would have taken.
Multiple sizes matter most when solvers recommend dramatically different sizes at significant frequency.
9♠ Turn
This is also true on a board like A♥K♥9♦ 9♠, where the complex strategy rarely uses a bet size other than 67% pot. In that case, simplifying to just 67% pot only makes a difference in the 4% of cases where the complex strategy would have done something else. Even then, the “something else” is just a slightly smaller or slightly larger bet (40% or 100% pot), which has only a slight effect on the EV.
K♠ Turn
As we saw on the flop, the cases where multiple sizes really matter are those where the complex strategy employs two or more dramatically different sizes at significant frequency; A♥K♥9♦ K♠ is a good example. The complex strategy bets 40% pot with 31.6% of hands and 200% pot with 14.7% of hands. The simple strategy loses the small bet and bets 200% pot with 24.3% of hands.
That means both strategies play about 68% of hands the same way. The simple strategy sacrifices EV with those 31.6% of hands that would play best as a small bet but must compromise by either checking or overbetting instead. The weaker King-x in UTG’s range strictly prefer a 40% pot bet in the complex strategy and have an EV of about 8.9bb. In the simple strategy, checking becomes their best option, earning just 8.3bb.
To be fair, there are a few hands that perform better in the simple strategy. Aces, for example, is a pure overbet in both strategies but expects to win more in the simple strategy because the overbetting range overall is weaker, giving BB more incentive to call or raise. But UTG has just three combos of Aces, and most other hands suffer for lack of more options.
The River
When last to act on the river, there is no room to make up the difference later. Unless your opponent check-raises, the bet you made is the bet you’re stuck with. Thus, multiple sizes matter most on the river. They matter so much that the solver automatically adds the option to go all-in on the river to ‘Automatic’ simulations.
Multiple sizes matter most on the river.
Here are 2 more charts comparing a simple strategy—where the solver automatically chooses a single bet size (plus all-in, as discussed above)—to a complex one with five bet size options. These strategies are for UTG’s river barrel after a 40% flop c-bet and 67% turn-barrel on an A♥K♥9♦ 9♠ board.
As with the turn, there’s a lot of checking and so many cases where both strategies take the same action. Yet a consistent gain in EV is apparent for the Complex strategy even when diluted by all those checks.
The largest difference appears to be for a rivered K♣, which makes sense. Just as we saw on a turned King, this card incentivizes UTG to use one very large size—all-in, on the river—with a more polar range and also a much smaller bet size to accommodate thinner value bets. Nodelocking to restrict UTG to only the all-in option further reduces UTG’s EV to 6.2bb.
Conclusion
Solvers offer an enormous amount of information, far too much for us humans to wrap our heads around. One pitfall of working with them is that you may become overwhelmed by the complexity and focus on the wrong things or just throw up your hands in frustration.
Solutions with multiple bet sizes are a great example of this. Especially on early streets, finding signals in the noise is challenging. These multiple sizes are not worthless—solvers don’t do anything without reason—but in most cases, their added value is small even when implemented perfectly. In the vast world of poker concepts, wrangling multiple bet sizes should not generally be your top study priority.
One framework for managing this complexity is making smaller circles: start with the big picture, progressing to greater degrees of refinement and detail as you master each stage. In this case, that process would look something like:
- Practice choosing a single bet size that is appropriate for a given spot. That means thinking less about what you want to accomplish with your specific hand and more about the underlying range dynamics: who has more equity, who has more nuts, what is the SPR, etc.
- Practice constructing betting ranges that are appropriate for the size you choose.
- Practice identifying situations where multiple bet sizes will provide especially high value. Start with river spots, as those are where multiple sizes make the biggest difference, then move back to the turn, then the flop.
- Repeat steps 1 and 2 using two bet sizes. Remember that these two sizes should be meaningfully different from one another; splitting between 40% and 66% pot isn’t generally worth the hassle.
This list may look simple, but (1) and (2) are enormous tasks. There are so many different situations in poker—in position, out of position, single-raised pots, 3-bet pots, etc.—that more casual players could spend years on these and never reach Step 3.
And that’s ok! Unless you find it intrinsically interesting to study multiple sizes, you will likely get a better return on your study time by focusing on other concepts.
Author
Andrew Brokos
Andrew Brokos has been a professional poker player, coach, and author for over 15 years. He co-hosts the Thinking Poker Podcast and is the author of the Play Optimal Poker books, among others.