Combinatorics Poker Puzzle
Today we have a special puzzle for you that will test your intuition as a poker player, and challenge your understanding of combinatorics.
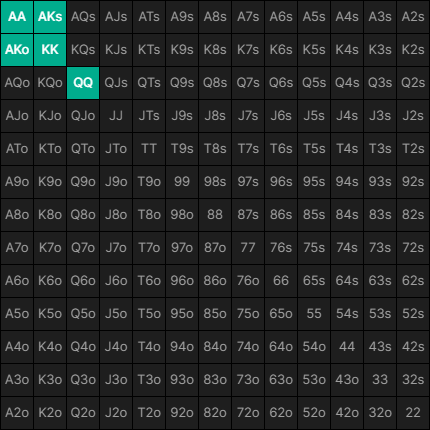
Six players go all-in preflop with a range of (QQ+, AK).
Questions:
- Can QQ win the pot? If so, how?
- Can KK win the pot? If so, how?
- Would you rather hold QQ, KK, or AKo in this scenario?
- A spectator places a side bet. They win the side bet if any A/K/Q lands on the board postflop. What are the chances that they win?
Please note that you do not need an equity calculator or any special software to answer these questions.
Answers:
Correct answer
The trick to answering these questions is to ask yourself how it is possible that 6 different players ended up with (QQ+, AK). When you consider card removal, the possibilities become quite limited.
There are only 12 cards in the deck that contain a Queen, King or an Ace.
6 players with two cards each will use up every king, queen, and ace in the deck.
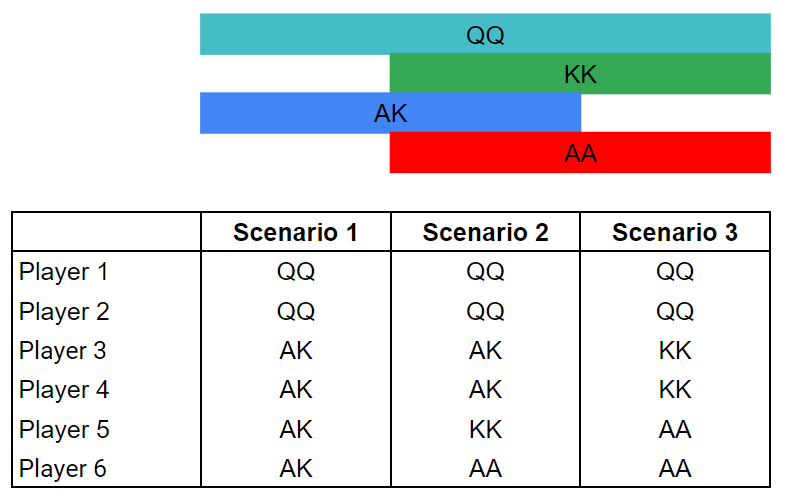
Now let’s ask how many ways can 6 players actually have these ranges. There are only 3 possibilities:
Can QQ win the pot? If so, how?
Yes, but only if it makes a straight flush! Two players are guaranteed to have QQ in all scenarios. All the aces and kings are in play, so winning with a regular flush is impossible. All queens are in play, making it impossible to outdraw better pairs.
Can KK win the pot? If so, how?
No, KK cannot win the pot. KK is always trying to outdraw AA. To do this, it must make a straight, a flush, or use a 3rd king. All the kings are in play, so it can’t use a 3rd king. All the queens are in play, so a straight is impossible. All the Aces are in play, so it can’t win with a flush. Therefore, KK cannot win the pot.
Would you rather hold QQ, KK, or AKo in this scenario?
QQ has substantially more equity than the other hands. Winning isn’t the only way to win the pot, you can also chop. ⅓ of the time QQ ends up in scenario 1, where you’re up against another QQ and 4 players with AK. This is very profitable for QQ since the AK block each other’s outs.
The only way KK can chop is if all 6 players chop via a straight on board.
AK is always up against 1 or 3 other AK’s. It can win with an ace-flush, and it can chop with a wheel straight. However, these events are far less likely to happen compared to QQ’s 1 in 3 chance of running into scenario 1.
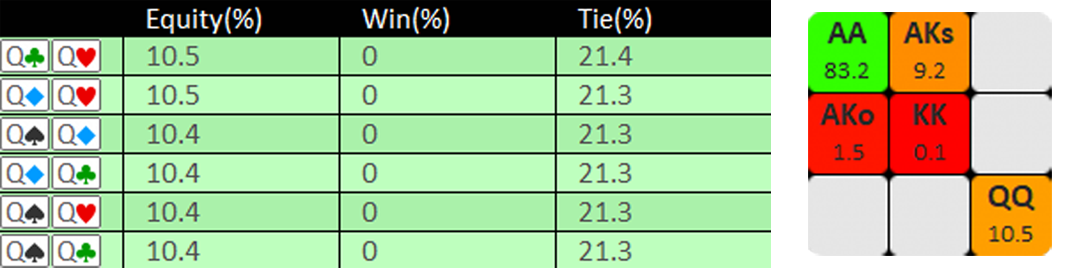
If we run a simple equity calculation, we see that QQ has substantially more equity than KK or AKo. However, this comes from the fact that QQ chops with the other QQ over 20% of the time.
A spectator places a side bet. They win the side bet if any A/K/Q lands on the board postflop. What are the chances that they win?
The probability is exactly zero, since all the aces, kings, and queens must be held by the 6 players.
Author
Tombos21
Tom is a long time poker theory enthusiast, GTO Wizard coach and YouTuber, and author of the Daily Dose of GTO.
Latest article
Responding to Donk-Bets at Final Tables
It’s scary to contest a pot against a covering stack when you have a high…
Donk-Betting As the Covering Stack in MTTs
Tournament poker generally incentivizes stack preservation and more conservative play than cash game poker, and…
Dominate the River in 3-Bet Pots OOP
Playing the river may seem scary. Pots, on average, have been swelling up big time…
Exploiting BBs Who Never Donk-Bet
In a single-raised pot (SRP), a BB caller should almost always check when out of…
Picking the Right Semi-Bluffs
As I often like to remind readers, I am not a professional poker player; I…
Playing Calls From the Button in Cash Games
When first beginning to study cash game poker strategy, there is a common refrain that…
Bringing It All Together: PKO Review
Throughout the past year, our writers have presented nine unique articles and videos outlining how…
What Factors Impact Ranges the Most in PKOs?
In our article “How Does ICM Impact PKO Strategy?“, we contrasted how PKO and Classic…
PKO vs Classic: Postflop Play
In our previous articles comparing PKO and Classic tournaments, we reviewed how to adapt our…
How Do Bounties Impact Our Flop Ranges When Covering?
The previous articles in our PKO series showed how preflop ranges that are adjusted for…
Short Stack Stealing on the Bubble
Open-raising on the bubble into players who cover you is scary. Savvy opponents will recognize…
Maximizing Monsters in Deep-Stacked Scenarios
Why did Dracula quit the game when Wolfman insisted on a mandatory straddle? — Why?…
Confronting Monsters Under the Bed in Poker
Do you hide from things that go bump in the night? Does the sight of…
Bullying the Blinds With Continuation Bets
A big stack in No Limit Hold‘em does not always carry a license to steal.…
A Comprehensive Guide to Playing Satelites
One of the most important inventions in poker that contributed to the growth of the…
A Comprehensive Guide to Playing Mystery Bounties
The Mystery Bounty format looked like a novelty event at first, but swiftly became a…
Leading Hands That Should Check-Call
The most consistent leak I have encountered live and online, and at a variety of…
Mastering Turn Play in 3-Bet Pots OOP
Playing the flop OOP in a 3-bet pot can be challenging. Turn play, however, is…
PKO Versus Classic: Responding to 3-Bets
One of the keys to adapting to new game formats, such as Progressive Knockout (PKO)…
PKO Versus Classic: Responding to a Preflop Open
One of the keys to adapting to new game formats, such as Progressive Knockout (PKO)…
Preflop Range Morphology
Morphology in poker is the study of shapes/forms of ranges. This domain of poker study…
The Five Imbalances of Exploitative Poker
One of the great modern debates in poker is GTO vs Exploitative strategy. It can…
PKO Versus Classic: Preflop RFI Range Comparisons
One of the keys to adapting to new game formats, such as Progressive Knockout (PKO)…
Why So Much? An Exploration of Larger-Than-Geometric Bet Sizing
Via toy games, it is easy to demonstrate that a player betting a perfectly polarized…
Slow-Playing
Slow-playing, like running a big bluff or making a heroic call, feels great when it…
MDF vs ICM: Rethinking Bluffing & Defense Strategies in MTTs
Minimum Defense Frequency (MDF) is, strictly speaking, the calling (and/or raising) frequency that makes your…
The Magic of Equity Buckets
One of the most daunting aspects of learning the modern game of poker, especially with…
Preflop Strategy in Straddled Pots
Many games allow “straddles,” where a player who is not in the blinds voluntarily posts…
The 5 Levels of Trainer Mastery for MTTs
Studying poker can be a challenge to both new and seasoned players. Tournament poker, in…
4-Bet Pots OOP as the Preflop Caller
4-bet pots are often uncomfortable to play. Some of the reasons include: — A lot…
Bounty Models Explained: Solving Knockout Tournaments
We’ve just rolled out a revolutionary update! You can now find optimal postflop ICM strategies…
Theoretical Breakthroughs in ICM
Today, we’ll share one of the most significant theoretical breakthroughs in tournament poker since the…
The Limitations of Nash Equilibrium in ICM Spots
In the complex world of poker tournaments, the Independent Chip Model (ICM) plays a pivotal…
Rake & Rakeback Explained: Optimize Your Poker Earnings
Rake is one of the main things that allows poker to distinguish itself as a…
From Gutshots to Airballs: Choosing Your Bluffs
Whenever you’re running a bluff, it’s reassuring to have a backup plan like some draw…
Crush 3-Bet Pots OOP in Cash Games
Did you know that 3-bet pots out of position (OOP) as the preflop aggressor make…
The Math of Multi-Street Bluffs
Bluffing is a fundamental skill in poker, blending deception with strategic calculation to sway the…
The Mechanics of C-Bet Sizing
What factors influence c-bet sizing on the flop? Is it fold equity, SPR, draw equity,…
Poker Insurance: Reducing Variance or Wasting Money?
Variance is what makes poker great. Without it, recreational players would not keep playing. Most…
Money Bubble vs Final Table Bubble
Is one bubble the same as another? Should we play more conservatively on the money…
Facing 3-Bets From Covering Stacks at the Final Table
The last thing you want when you have a nice stack at the final table…
Poker Staking Essentials
One of the great ‘through the looking glass’ moments for any poker player is when…
A Poker Player’s Guide to Conquering Cognitive Biases – Part 2
In the past, I’ve written about gambling biases that can affect how you play and…
The 5 Levels of Trainer Mastery for Cash Games
We’ve created over 40 custom drills for this article! Though all drills are accessible through…
How To Review ICM Preflop Ranges
In a sense, tournaments could be considered the more complex format compared to cash games.…
Calling Down Over-Bluffed Lines in Lower Limits
If you are playing low stakes, chances are you have a plummeting red line in…
A Poker Player’s Guide to Conquering Cognitive Biases – Part 1
In my article on confirmation bias, I mentioned that there are many cognitive biases and…
Exploiting Cold Callers Who Stab Too Much
In single-raised pots (SRPs) between an in position (IP) raiser and an out of position…
Using the 80/20 Rule in Poker
The Pareto principle, or the ‘80/20 Rule’, is an economic theory that, when you learn…
Attacking Aggressive Opponents When They Check Back Flop
Playing out of position (OOP) is hard. Playing out of position against an aggressive opponent…
Buying the Showdown
This article was inspired by Mark, who submitted a question to my podcast about a…
Barreling as IP Cold-Caller
You cold-called a preflop raise. That’s scary. You bet into a check from the preflop…
How Confirmation Bias Impacts Poker Study
There are a great number of cognitive biases, mental models, and heuristics that I plan…
A Champion’s Guide to Knockout Poker Formats
If you’ve opened any online poker client recently you will have seen an explosion of…
Pushing Equity With Small Bets
One of the most memorable pieces of poker wisdom I ever received came from my…
Turn Check-Raise Heuristics
Dealing with turn aggression is an area many players find difficult, which is an excellent…
Aggregate Flop Strategy: SB C-Betting in SRP
Continuation betting from the SB does not follow the usual patterns for out of position…
The Power of the Hypergeometric Bet
What size should we bet with our value and bluffs? When our range is perfectly…
The Limits of Nodelocking
GTO Wizard’s nodelocking feature is where the theory meets the practical; you can study how…
Limp-Called Pot as BB
My favorite way to study with GTO Wizard is to approach it experimentally, using the…
Why Not Shove?
You’re in the money in an MTT but still a long way from the final…
What We Can Learn From Outlier Hands
The worst way to use a tool like GTO Wizard is to simply ‘line-check’ how…
Building Exploits From Showdown
Understanding how and when to exploit opponents at a live poker table is a delicate…
Navigating Nasty Rivers Out of Position
Playing out of position (OOP) is hard. It’s fundamentally disadvantageous to act on each street…
Crack the Shell of Nut Draw Strategy
Nut draws hold obvious appeal as betting and raising candidates. They benefit from fold equity,…
Preflop Raise Sizing: Examining 2 Key Factors
It amazes me that, after nearly twenty years of playing no-limit hold ‘em professionally, I…
How to Handle Loose-Passive Limpers
Solver charts and presolved solutions do not offer much in the way of explicit guidance…
Top 5 Mistakes in Spin & Gos
As a Spin and Go poker coach, I regularly encounter common mistakes that players make,…
An Introduction to Spin & Gos
I was playing Tournaments for the first decade of my career. But after my first…
Relationships and Poker
In my more than 15 years of poker coaching, I’ve helped hundreds of clients improve…
Do Multiple Sizes Matter?
Should I work out the other tools or just stick to the crowbar? Solver results…
The Science of Learning Applied to GTO Wizard
The way we were taught to study in schools was flawed and has negatively impacted…
Check-Raising a Single Pair
In this article, I will address a question raised by Twitter/X user ’Matt Riley’, who…
The Turn Probe Bet
Imagine yourself defending as the BB caller vs BTN preflop raiser in a 100bb cash…
When To Encourage Multiway Pots in PKOs
I was recently shown this fascinating PKO hand from the GTO Wizard PKO library. Somebody…
Protect Equity and Prosper
When we think about the best hands to bet in a given situation, we tend…
Do Solvers Have Targets?
Targeting has long been a staple of exploitative poker thinking. When you’re value betting against…
Disciplining Big Blind in Limped Pots
When the BTN open-limps off a short stack, the postflop play against the BB should…
I’d Rather Be Drawing
Which is the better hand on a K♥8♦5♦ flop: K♠T♣ or 7♥6♥? OK, I’ll admit…
The Curious Case of Open-Limping Buttons
Before the advent of solvers, open-limping was considered the province of passive, gambley recreational players…
Cleaning Out Sticky IP Callers
A “sticky” player on your left, one who calls your preflop raises too often and…
Defending Against Tiny 3-Bets
Tournament poker is about precision. Cash games, where stacks typically run into the hundreds of…
Heads up! Exploiting SB’s Preflop Mistakes
Heads up (HU) tournament play presents unique challenges to the average player. Many tournament players,…
C-Betting As the OOP Preflop Raiser
Position is an extremely valuable advantage in poker. Most players would describe the comfort zone…
Overchoice: Making Sense of Multiple Sizings
Solver solutions with multiple bet sizes often involve a lot of mixing between those sizes,…
River Refinements: When Your Opponent Won’t Check-Raise
One of the biggest strategic differences between playing in versus out of position involves betting…
Turn Barreling in 3-Bet Pots
There are two articles on the GTO Wizard blog that make good prerequisites to this…
The Right Way To Think About Protection
Suppose Paul the Protector is in a 200bb cash game and opens A♠A♣ in the…
The Importance of Board Coverage
The first public version of the GTO Wizard announced AI upgrade already has some useful…
How To Adjust When Villain Has No Bluffs
“They always have it!” is a common, semi-joking expression in poker to describe the tendency…
Adjusting on Later Streets After Exploiting Flop
The key to exploiting opponents profitably is knowing when to stop. I’m not referring to…
C-Betting IP vs Passive Poker Players
A preflop raiser enjoys a significant range advantage over a BB caller, enabling them to…
C-Betting Against ICM Preflop Ranges
You raise from early position (EP) in a multi-table tournament and the BB calls. Both…
The Art of Bluff Catching
Bluff catching—calling a bet with a modest hand which you expect to win only if…
Exploiting Excessive C-Betting by IP
On some flops, it is simply not possible for the preflop raiser to continuation bet…
Is Limping Pimping?
In a past Discord post, one of our members noted that an upside of implementing…
Exploiting Excessive C-Betting by OOP
A preflop raiser who continuation bets too often is always a potential target for exploitation,…
Preflop Button Mastery in PKOs
Playing from the Button presents many unique opportunities in any tournament format, especially in PKOs.…
The Worst Turn Card
Greetings from GTO land. In today’s article, we will use the Turn Reports feature to…
Navigating Range Disadvantage as the 3-Bettor
Picture this: We’re playing a NL500 6-max cash game, and we’ve won a few pots,…
Mastering Three-Bet Pots In Position in MTTs
Playing in position against a three-better is a lesson in playing to your advantages. As…
Mastering Three-Bet Pots Out of Position in MTTs
Three-bet pots are scary. Playing out of position is scary. Put them together, and you’ve…
The Greatest Final Table in Triton History
Today, we’ll examine one of the most epic final table battles I’ve ever witnessed! Our…
Mastering Thin Value Bets in Checked-Down Pots
Valuing your hand appropriately—determining whether it’s strong enough to value bet or so weak you…
Maximizing Value on Monotone Flops
Monotone flops tend to provoke great anxiety among poker players. It’s easy to imagine that…
How to Defend Against Turn Donk Bets
Responding effectively to donk bets on the turn is tricky;, there’s no getting around that.…
How and Why You Should Use Turn Donk Bets
Donk betting–taking the betting lead away from the previous street’s aggressor–on the flop is rarely…
How Stack Sizes Change Your Range
In this series, we have looked at factors that can influence ranges in otherwise identical…
How to Leverage GTO Wizard’s EV Comparison Tool
With the advent of solvers, some troubling new turns of phrase have entered the poker…
Should You Ever Cold Call a 3-Bet?
When there’s been a raise and re-raise before the action is on you, you will…
When ICM Breaks Down
If you have read my previous GTO Wizard articles and my books, you’ll know I…
When Is It Correct To Fold AA Preflop?
One of the criticisms of ICM is that it is boring and robotic. In my…
OOP C-betting vs Loose Cold-callers
In a previous GTO Wizard article, I asserted that “Playing against an in-position cold-caller is…
Short-Stacked Play in MTTs
Playing a short stack well is an essential tournament skill. It is extremely rare to…
When To Ladder in Tournaments
In my last two articles, I wrote about the effect field size and payout structure…
How Payout Structures Impact ICM
Last time we discussed the ICM considerations in game selection, we looked at field size,…
C-Betting IP in 3-Bet Pots
When you three-bet before the flop and the original raiser calls from out of position,…
C-Betting OOP in 3-Bet Pots
Continuation betting from out of position can be a dicey proposition in single-raised pots. Cold…
Dynamic Sizing: A GTO Breakthrough
Dynamic Sizing is a revolutionary new poker algorithm that automatically simplifies your strategy with the…
Dynamic Sizing Benchmarks
Dynamic Sizing is a revolutionary new poker algorithm that automatically simplifies your strategy with the…
Understanding The Impact Of Field Size On ICM In Poker
When people talk about game selection in multi-table tournaments (MTTs), they invariably talk about the…
Defending vs BB Check-Raise on Paired Flops
This is a companion piece to Attacking Paired Flops from the BB; you will get…
Mastering PKO Final Tables
Final tables can be the most exciting and rewarding phase of a tournament, and being…
Attacking Paired Flops From the BB
Paired flops present unique challenges to both a preflop raiser and a BB caller. The…
KK vs QQ vs JJ at WSOP Main Event
With only fourteen players remaining in the 2023 WSOP Main Event and blinds of 400K/800K/800K,…
Responding to BB Squeezes
You open raise, someone calls, and the BB squeezes. How should you construct your strategy?…
Crushing a Top HUNL Poker Bot
In 2022, Philippe Beardsell and Marc-Antoine Provost, a team of Canadian programmers from Quebec, developed…
GTO Wizard AI Explained
We are excited to introduce GTO Wizard AI, formerly known as Ruse, the world’s best…
GTO Wizard AI Benchmarks
GTO Wizard has combined the power of artificial intelligence with traditional solving methods to bring…
Table Management in PKOs
Perhaps the most important strategic consideration in Progressive Knockout Tournaments (PKOs) is making sure you…
Overcalling From the BB
In poker, overcalling refers to calling a bet or raise after another player has also…
Understanding Which Mistakes Cost You the Most Money
I am fortunate enough to have worked for many years with the mental game coach…
Overbetting The Flop in Cash Games
Although most commonly analyzed on turns and rivers, flop overbetting can be a devastating weapon…
Using New Skills at the Poker Table
How many times has it happened to you that you make a mistake only to…
Flatting Ace-X Hands Shortstacked
Playing out of position is tricky, but it’s an essential part of tournament play. With…
Playing Limped Pots as the BB in MTTs
Success as the BB in limped pots begins before the flop. The BB’s equilibrium strategy…
The Absurd Game Theory of Chopped Boards
A “chopped board” in poker is one where the community cards make up the best…
Playing Limped Pots as the SB in MTTs
MTT confrontations between the small blind and big blind force no-limit players into uncomfortable situations,…
The Art of Learning Poker
In his book The Art of Learning, chess and Push Hands champion Josh Waitzkin describes…
Is Donk Betting for Donkeys?
“Donk betting”, or betting from out of position into the player who was the aggressor…
Delayed C-Betting
This is a companion piece to Probe Betting. It stands on its own, but understanding…
Probe Betting
As far as rules of thumb go in poker, “check to the raiser” is a…
ICM and Blind Battles: The Big Blind
This is a companion piece to this article on the SB’s strategy for blind vs…
ICM and Blind Battles: The Small Blind
ICM incentivizes more conservative play, which means that at stages of the tournament where risk…
The Initial Bettor’s Advantage
The mathematics of poker holds a little-known secret: the first bettor enjoys better bluffing odds…
Mastering the Chiplead: The Scalpel and the Sledgehammer
When you have a lot of chips at a final table or in another situation…
Flop Heuristics: IP C-Betting in Cash Games
Our never-ending quest for money and fame leads us to the flop. We open the…
How ICM Impacts Restealing From The Blinds
When I first started working with preflop solves, one of the features I found most…
The ICM Benefits of Late Registration in Poker Tournaments
Why do so many professional poker players register late for tournaments when they clearly would…
Flop Heuristics: OOP C-Betting in MTTs
Playing against an in-position cold-caller is dramatically different–and dramatically more difficult–than playing against a caller…
Counterintuitive Calls
Solver outputs such as those provided by GTO Wizard are models of no-limit hold ‘em,…
How To Negotiate Final Table Deals
Most people’s first introduction to the Independent Chip Model (ICM) is not from studying bubble…
How Does ICM Impact PKO Strategy?
If you have read The Theory of Progressive Knockout Tournaments you already know why we…
Understanding Blockers in Poker
Often when looking through a solver’s meticulously crafted grid of deception, one of the following…
Flop Heuristics: IP Cold-Caller in MTTs
A Cold-call refers to the act of calling a preflop raise when you don’t close…
Flop Heuristics: IP C-Betting in MTTs
In the world of poker, the flop is a crucial stage of the game that…
Flop Heuristics for Defending the Blinds in MTTs
The field of Game Theoretically Optimal poker is extensive, and thus, to simplify our strategy,…
Multiway strategy in Progressive Knockout Tournaments
Progressive Knockout (PKO) tournaments are much more complex than traditional MTTs. The fact that players…
How To Calculate Raises In Poker
One of the most frequently asked questions in poker is how to calculate the size…
Principles of River Play
The river offers the least complicated strategy of any betting street. With no further cards…
Exploitative Dynamics
GTO solutions are designed to be unexploitable, performing reasonably well no matter how your opponents…
How ICM Impacts Postflop Strategy
Most players understand how the Independent Chip Model (ICM) in poker impacts their strategy preflop,…
10 Tips for Multiway Pots in Poker
While lots of work has been placed into research and explanation of heads-up pot strategy,…
What is the Bubble Factor in poker tournaments?
The Independent Chip Model (ICM) shows us the real money implications of tournament chip decisions.…
The Theory of Progressive Knockout Tournaments
In poker, a PKO (Progressive Knockout) tournament is a type of tournament where a portion…
How To Analyze Turn Textures In Poker
Master the art of turn analysis in poker. Understand how the turn card changes the…
Principles of Turn Strategy
Learn the principles of turn strategy in poker and discover what makes the turn unique.…
Poker Strategies: Tournaments vs. Cash Games
Tournament poker is not as different from cash game poker as people sometimes assume. Most…
How Solvers Work
A Game Theory Optimal solver is an algorithm that calculates the best possible poker strategy.…
The Most Powerful Play in Poker
The central strategic implication of stack depth is the question of how much equity a…
When does ICM become significant in MTTs?
The Independent Chip Model (ICM) was invented in 1987 by M. Malmuth and is one…
How to Study GTO Solutions
Tools like GTO Wizard and other solvers should not be used to memorize specific strategies.…
Principles of GTO
Game theory, or GTO (for Game Theoretically Optimal), is best understood not as a rigid…
Interpreting Equity Distributions
GTO Wizard’s range vs range equity distribution graphs are an excellent tool for visualizing which…
What is Leverage in poker?
Leverage refers to the risk of future betting. When you call a bet on the…
Reasons for value betting in poker
You’re probably accustomed to thinking of bets as either value or bluff. In this taxonomy,…
The Science of Poker Performance
Poker is a game of small edges and big swings. Every hand is an investment…
What is Valor in poker?
Can a poker hand be courageous? How does your ability to value bet future streets…
Pot Geometry
“Pot Geometry” refers to betting an equal fraction of the pot on each street, such…
A Beginner’s Guide to Poker Combinatorics
Combinatorics is a fancy term for evaluating the number of possible “combinations” (combos) of any…
Stack-to-pot ratio
Stack-to-pot ratio, or SPR, is a way of measuring how deep the effective stack is…
Equity Realization
In poker jargon, equity expresses how much of the pot a hand will win, on…
Variance and Bankroll Management
Variance and Bankroll Management. Vital Soft Skills for Every Poker Player.
How to Become a GTO Wizard
Welcome to the wonderful world of game theory optimal poker! This article will serve as…
The Three Laws of Indifference
Indifference in poker is one of the most misunderstood concepts. The word “indifference” means that…
Poker subsets and abstractions
An “abstraction” is a way to simplify the game of poker. This game is so…
Mathematical Misconceptions in Poker
Pot Odds and MDF are foundational mathematical formulas in poker.
How to solve toy games
Poker is a complicated game. It’s impossible to calculate GTO strategies on the fly. By…
The Value of Fold Equity – Experiment
The term “fold equity” is ambiguous in the poker community. Firstly, it’s an EV equation,…
MDF & Alpha
MDF & Alpha. Minimum Defence Frequency and Alpha are metrics on poker that determine how…
What are Pot Odds in poker?
Pot odds are a fundamental calculation in poker. In the simplest terms, pot odds tell…
Does your range affect your strategy?
Advanced players will often tell you that your range affects your strategy.
Visualizing implied odds
Implied odds are the value you expect to gain over and above your raw equity.…
ICM Basics
As a tournament player, you may have heard about the concept of “ICM”, but what…
What is Equity in Poker?
The term “Equity” is ubiquitous throughout poker theory. Equity refers to your chances of winning…
Range Morphology
“Morphology” is the study of form or structure. You’ve probably heard terms thrown around such…
What is Expected Value in Poker?
Expected value (EV) is the most fundamental metric in poker. Every decision you make is…
Why doesn’t my solution match GTO Wizard?
So, you’ve got your own solutions to some spot, compared it to GTO Wizard, and…
Understanding Nash Distance
Understanding Nash Distance. One of the most common questions when studying with solvers is “Why…
Combinatorics Poker Puzzle
Today we have a special puzzle for you that will test your intuition as a…
The 10 Most Important Concepts for New Poker Players
The 10 Most Important Concepts for New Poker Players. Fundamentals are one of the most…
What is GTO in Poker?
The meaning of GTO in poker is Game Theory Optimal. Game theory is a study…
What does GTO aim to achieve?
So what exactly is a GTO strategy? What makes it “unexploitable”? What does it try…