The Three Laws of Indifference

Indifference in poker is one of the most misunderstood concepts. The word “indifference” means that two or more actions have the same value. Therefore, understanding why indifference plays such a huge role in game theory optimal poker is critical to learning poker theory.

Interpreting GTO solutions is often more art than science 🔬 It’s often a subjective process requiring a combination of intuition and scientific analysis. There are many rules of thumb and heuristics but few hard laws in Game Theory Optimal Poker. Therefore, it’s essential to learn the absolute hard laws of indifference to separate fact from fiction.

This article will outline the few fundamental “hard laws” of indifference that structure Nash Equilibrium. These laws apply to both GTO and all poker strategies, including exploitative styles.

The Law of Selfish EV

No hand will sacrifice value to improve the value of the rest of your range. A perfect strategy always takes the highest EV action with each hand in every spot.

Think about it. Why would you intentionally play a losing move? Why not just always play the best move? This should be self-evident. There is no such thing as playing a -EV move to improve the expected value of the rest of your range. If a hand is a losing call, then there’s no point calling and losing money.

The consequence of Law 1 is Law 2: The Law of Selfish EV implies the Law of Indifference.

No hand will sacrifice value to improve the value of the rest of your range. A perfect strategy always takes the highest EV action with each hand in every spot.

The consequence of Law 1 is Law 2: The Law of Selfish EV implies the Law of Indifference.

The Law of Indifference

If a hand mixes multiple actions, those actions will have the same value. For example, if a hand mixes between calls and folds, then calling must be worth 0EV. If a nutted hand mixes between calling and raising, then trapping must be worth as much as fast-playing.

Conversely, any hand with actions that have the same EV must be indifferent between those actions. If calling is worth $3, and raising is worth $3, then you must be indifferent between calling and raising. Why would you ever choose a lower EV action? If calling is worth more than folding, then simply never fold.

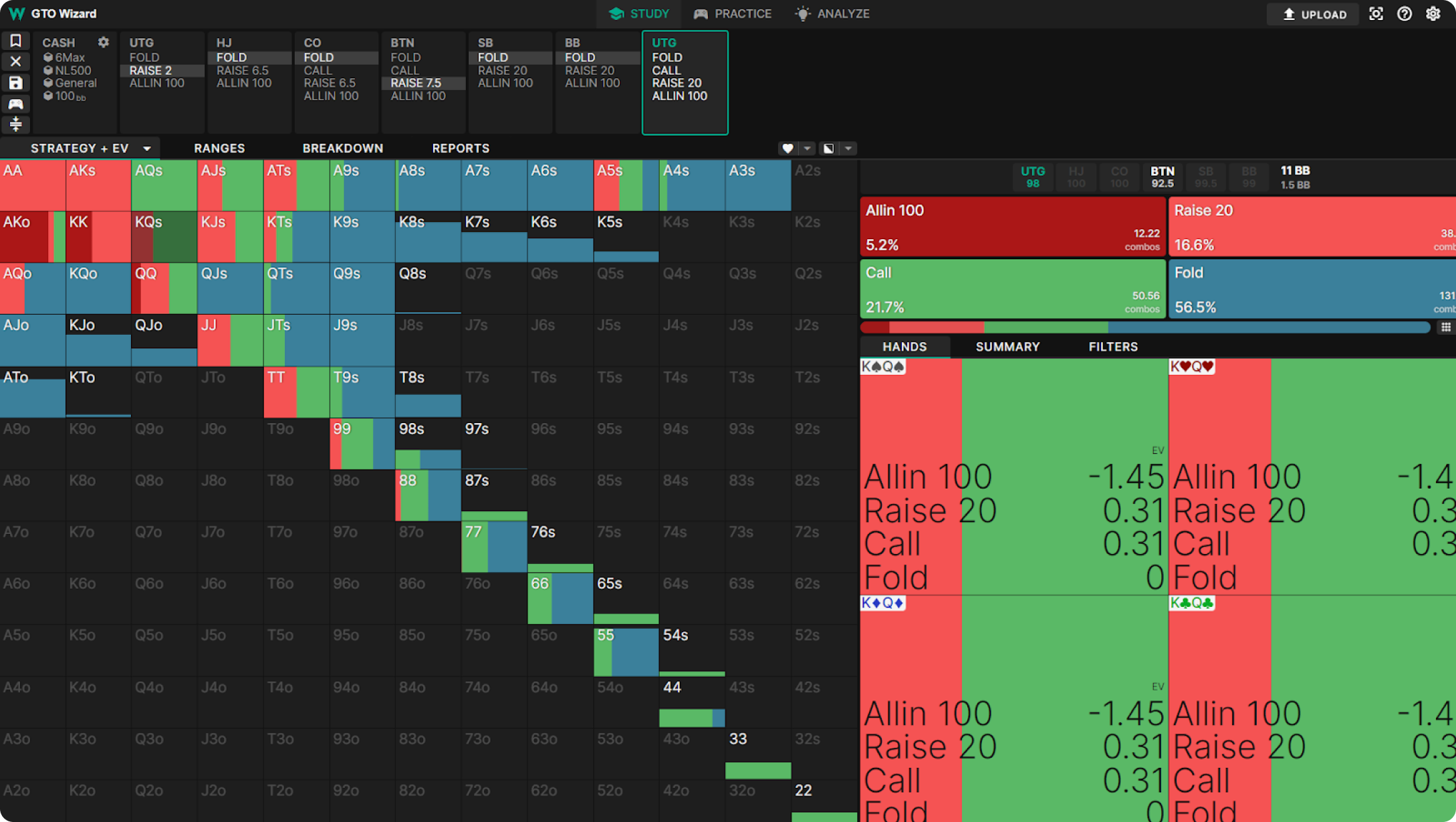
Let’s look at an example. UTG opens, BTN 3bets. Action folds to UTG, who holds KQs:

Here I’ve selected the “Strategy+EV” view. We can see that KQs has an EV of 0.31bb when 4betting or calling. We can see that it mixes between both actions. Therefore, it is indifferent between those two actions.

We see many indifferent actions. A5s (EV 0) is indifferent between folding, calling, and 4betting. QQ (EV 42.7) is indifferent between shoving, 4betting, and calling. 88 (EV 0) is indifferent between folding and calling. Very few hands are taking pure actions. The strategy is mixed in this way to remain unexploitable against all possible counterstrategies.

This law applies regardless of what strategies are in place. This applies to GTO strategies, exploitative strategies, and every strategy in between. If you plug in your opponent’s imperfect and exploitable strategy, then some hands will inevitably still face indifferent decisions. Although exploitative simulations tend to result in more pure actions, as fewer decisions are perfectly indifferent against imperfect strategies. Indifference does not rely on GTO, it only relies on your opponent’s strategy.

Sometimes solvers suggest -EV actions. This is a result of noise! If you solve to high enough accuracy, that noise goes away. True equilibrium would never intentionally choose a lower EV action. You can learn more about solver noise in this article.

The consequence of Law 2 is Law 3: The Law of Indifference implies the Law of Fixed Strategies.

The Law of Fixed Strategies

Changing mixtures between indifferent actions cannot lose value against a fixed strategy. Mixing mistakes can only be exploited if the opposition adapts their strategy.

Okay, but what is a mixing mistake, and what is a fixed strategy?

A mixing mistake means moving hands between indifferent decisions.
A fixed strategy (like GTO) doesn’t change or adapt to its opponent.

Okay, but if my range on later streets changes, wouldn’t my EV change?

Expected value is zero-sum. For one player to gain, the other has to lose. So, if you’re mixing incorrectly between two decisions with the same EV, how would one player gain anything without changing their strategy? The EV of your hand encompasses decisions on later streets.

One major exception to this rule is when EV is not zero-sum. Rake cuts into your EV, so mixing mistakes can increase or decrease the total sum of rake paid by both players.

Think about it this way. All you’ve done is moved a hand between two actions that have the same EV. You’ve simply moved a hand between two indifferent decisions. Since both those actions have the same value against your opponent’s strategy, they cannot gain unless villain changes their strategy!

For example, let’s assume KK is supposed to call 30% of the time and raise 70% of the time to be unexploitable. But instead, you split 50% / 50% – that is a mixing mistake. However, both actions have the same EV (Law 2). Therefore, if the opponent doesn’t change their strategy, then any mixture between calling and raising will result in the same payoff! However, this doesn’t give you a licence to do whatever you want. Your new strategy is exploitable. If the opponent adjusts, they can punish your mixing mistake.

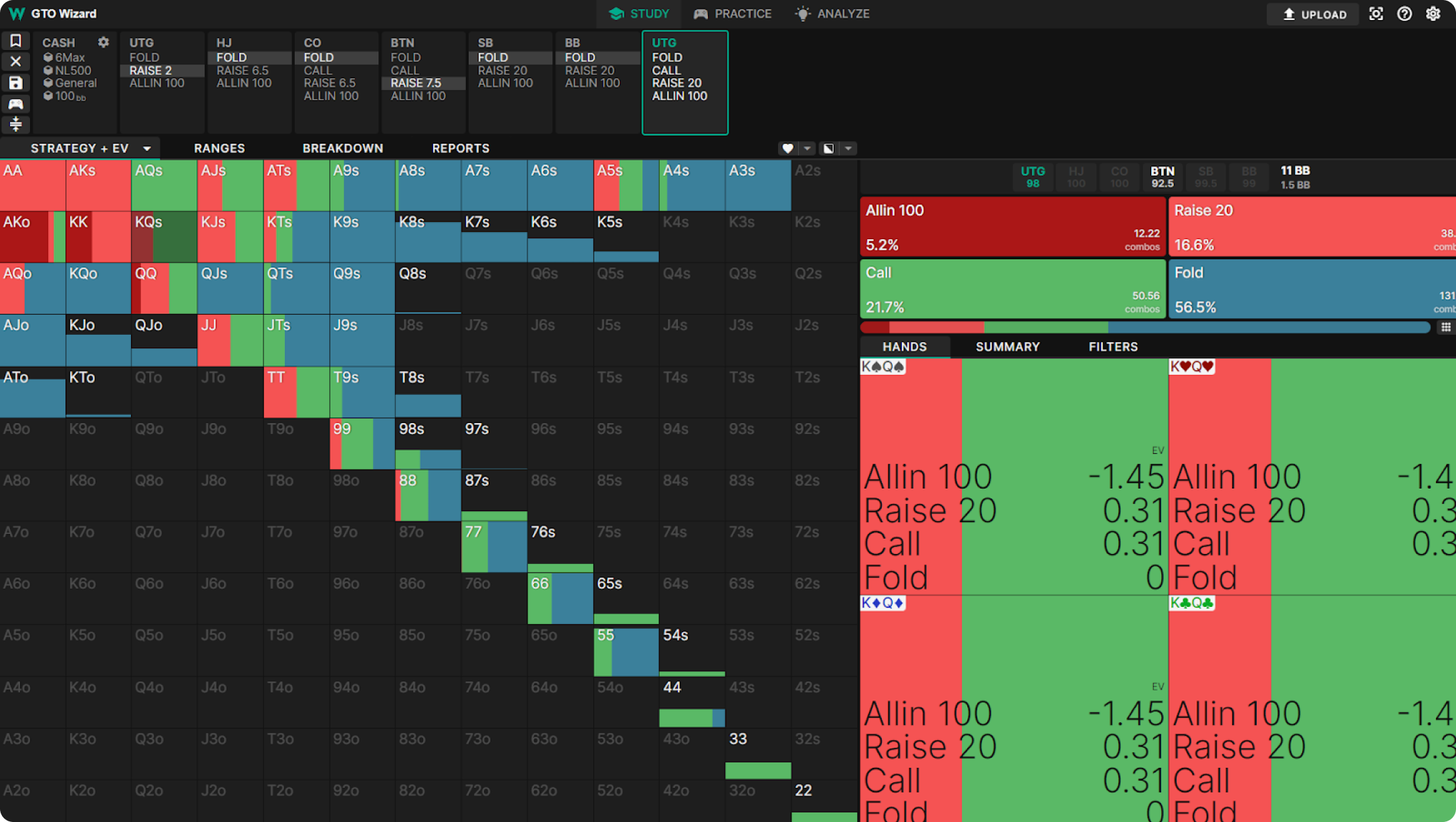
Let’s go back to the previous example. UTG opens, BTN 3bets, folds to UTG:

Let’s imagine that you folded every hand which folds at any frequency. Would your EV change?
No. All you’ve done is moved more 0EV hands into the fold line instead of other lines. However, BTN could exploit your overfolding by 3betting much wider. In this case, you’d be folding hands that were actually +EV continues, which would cost you value. Note that BTN only gains against your mixing mistake when they change their strategy.

To understand this concept, you need to realize one crucial detail: The best action with your hand is determined solely by your opponent’s strategy. The indifference regions in your range are purely a function of how your opponent plays. Therefore, they need to change their strategy to change what hands/actions are indifferent within your range. Learn more about this concept by reading this article.

GTO is a fixed strategy. Therefore, it doesn’t gain against mixing mistakes. However, it does gain against “pure mistakes”. Any action that loses money against a fixed strategy is a “pure mistake”. There’s a common misconception that GTO gains against “any mistake”. However, this isn’t true, as GTO can only gain against pure mistakes. Fret not, though, as even high-level pros make many pure mistakes; poker is hard! Watch this video to learn more.

FAQ

The following Frequently Asked Questions should cover most fundamental topics about GTO. Of course, feel free to contact our Discord Server with any questions!

What about metagame strategies?

It’s possible to make an argument for -EV plays if it will induce mistakes from your opponents later on. For example, playing a -EV bluff to develop a loose image might be valid if it causes others to make future mistakes against you. But this is not valid logic in GTO because there are no future mistakes to be made. Furthermore, you could argue that if a -EV “mistake” is the highest EV move in the long term, then it’s not actually a mistake but the correct exploitative strategy and, therefore, +EV. Reframing the timeline from one hand to a lifetime of hands resolves the paradox of -EV metagame moves.

Does GTO ever make a -EV play?

Yes! But only if your opponents are making mistakes. For example, GTO might suggest 4bet shoving KK. It will suggest this even if your opponents are only 3betting AA. This is clearly a losing play. But, your opponents are losing even more value by not raising their other premium hands. Anyone can gain against GTO in one part of the game tree at the expense of the rest of their strategy.

If you know with certainty that your opponents are only raising AA, then exploit them by adapting your strategy. But even if you didn’t adapt, they are still making pure mistakes by losing value with KK, QQ, etc.

Can you beat GTO?

No. The definition of Nash Equilibrium is that no player can unilaterally change their strategy to increase their EV. You can increase the EV of some lines at the expense of others, but beating GTO is impossible by definition.

One notable exception is that GTO doesn’t guarantee unexploitability in multiway pots. No strategy is unexploitable in multiway pots.

Why does the solver make -EV moves, or not choose the highest EV action?

This is a result of solver noise. In practice, solvers do not reach perfect accuracy, which results in noise in the solutions. Learn more about solver noise in this article.

What is a mixing mistake vs pure mistake?

A mixing mistake (sometimes called a frequency mistake) is mixing indifferent actions at incorrect frequencies. For example, if KK is supposed to call 30% and raise 70%, but you split 50%/50%, that’s a mixing mistake. It is specific to actions taken with unique combos, rather than your entire strategy.

Pure mistakes lose money against fixed strategies.
Mixing mistakes only lose money if the opposition adjusts to exploit that mistake.

What is a fixed strategy?

A fixed strategy does not change in response to its opposition. A fixed strategy always plays the same way in the same spot. GTO is an example of a fixed strategy. Conversely, a dynamic strategy will adapt and change to its opposition. Read more in this article.

If mixing mistakes aren’t punished, then why can’t I just rangebet/check everything?

Mixing mistakes are exploitable. But it requires your opponents to use something other than the GTO strategy. This adaptation from GTO can be intentional or just their natural playstyle. Be careful not to oversimplify under the guise of indifferent mixing mistakes.

For example, calling all indifferent bluff-catchers on the river is easily exploited by value-heavy strategies. Overfolding mixed folds against a flop check-raise is easily exploited by over-bluffing.

Watch this video to learn more.

If GTO doesn’t gain from mixing mistakes, then how does GTO make money?

GTO gains anytime your opponents make a “pure mistake”. Pure mistakes lose money against fixed strategies. A pure mistake is any action with some hand that strictly loses EV against your opponent’s current strategy.