The Math of Multi-Street Bluffs
Bluffing is a fundamental skill in poker, blending deception with strategic calculation to sway the outcomes of hands. While numerous resources delve into the basics of bluffing, few explore the theory behind triple-barrel bluffing.
In this article, we explore the math of multi-street bluffing in poker. Specifically, how to calculate the expected value (EV) of bluffing across multiple streets.
Join us in the investigation to uncover the mathematical underpinnings that elevate bluffing from an intuitive gamble to a calculated strategy.
The Basics: Single-Street Bluffs
The basic theory of a single-street bluff is straightforward:
- Calculate the Minimum Defense Frequency (MDF)
- For your bluff to be profitable, your opponent needs to fold more often than (1 – MDF)
The expected value of a pure bluffPure Bluff
A pure bluff is a hand that can never win at showdown. is also easy to calculate:
EV (Bluff) = Fold%(Pot) – Defend%(Bet)
If your EV > 0, then you have a profitable pure bluff. Simple!
But here’s the thing:
If your bluff gets called (before the river), you don’t need to give up. You have the option to continue bluffing on later streets.
How does that change the math?
Quiz
Let’s test your intuitive understanding with a simple toy game:
You hold a pure bluffPure Bluff
A pure bluff is a hand that can never win at showdown. on the flop and are considering a triple-barrel bluff (of pot-sized bets). Villain always calls flop and turn. How often do they have to fold the river for your triple-barrel to break even?
- Fold 50%
- Fold 61%
- Fold 72%
- Fold 83%
C) Fold 72%
Many players would have guessed (a), assuming that we only need them to fold at least 50% (= 1 – MDF) of the time on the river, in order for a pot-sized 3-street (pure) bluff to break even. However, this doesn’t account for the money you’ve lost bluffing on the flop and turn. You don’t just need to break even on the river, you need the river to be so profitable that it makes up for all the losses you accumulated on your way to the river in the first place.
Explanation
In order for triple-barreling to be +EV, they need to be folding a ton on the river so that you can recuperate your lost flop and turn bets. Remember, you’re not trying to break even on your standalone river play, you want the entire line from flop→river to be (at least) breakeven.
So how does one calculate the right answer? Track contributions!
If the starting pot is 1, you bet (1, 3, 9) on (flop, turn, river). If your triple barrel gets called down, you’ll end up losing (1+3+9) = 13 starting pots. If it’s successful, you’ll gain (1+1+3) = 5 starting pots. So you’re risking 13 to win 5. Converting the odds to an implied probability: 13:5 = 13 / (13 + 5) = 72.2%
- Starting pot = 1
- Gain if we get a fold = starting pot + villain’s contributions = (1) + (1 + 3) = 5
- Loss if we get a call = hero’s contributions = 1 + 3 + 9 = 13
- You’re risking 13 to win 5
- Breakeven River Fold% = Risk / (Risk + Reward) = 13 / (13 + 5) = 72.2%
They need to fold 72.2% of the time to our river bet, just to break even on a pot-sized triple-barrel bluff. Anything less than that, and you’d be better off giving up on the flop.
Generally speaking, multi-street bluffs offer a worse risk-reward ratio than single-street bluffs, because you end up risking more than you stand to gain.
But this is a contrived example! No one is calling 100% of the time on flop and turn, just to fold ¾ of the time on the river. Let’s try a more realistic but also more complex example next.
The Math of Multi-Street Bluffs
Now, we will walk through the math of a multi-street bluff to handle more realistic scenarios.
What follows is not meant for over-the-table calculations. Rather, we recommend examining population tendencies and using a spreadsheet calculator to find over-folded lines.
To simplify things, we’ll make three assumptions:
I.
II.
III.
Your bluff always loses when you check
Your bluff always loses when it gets called down
Villain will only call or fold
Given these assumptions, there are only four strategies to choose from:
- Check: Give up immediately, lose nothing.
- Bet → Check: Bet once with the intention of giving up on the turn if called.
- Bet → Bet → Check: Bet twice with the intention of giving up on the river if called.
- Bet → Bet → Bet: Bet thrice with no intention of giving up.
To simplify things, we’ll make three assumptions:
I. Your bluff always loses when you check
II. Your bluff always loses when it gets called down
III. Villain will only call or fold
Given these assumptions, there are only four strategies to choose from:
- Check: Give up immediately, lose nothing.
- Bet → Check: Bet once with the intention of giving up on the turn if called.
- Bet → Bet → Check: Bet twice with the intention of giving up on the river if called.
- Bet → Bet → Bet: Bet thrice with no intention of giving up.
We will calculate and compare the EV of each strategy and choose the most profitable one.
Strategy (1) Check
This strategy’s EV is just 0 because we’re measuring EV relative to this decision point. If you give up immediately, you lose the hand without investing further into this bluff.
EV (Check) = 0
Strategy (2) Bet → Check
The expected value of (2)—betting once with the intention of giving up on the turn—is just the standard single-street calculation:
Multiply the probability (p) and value (v) of each event, then add them together to find the expected value:
EV (Bet → Check) = p₁v₁ + p₂v₂
Written out explicitly:
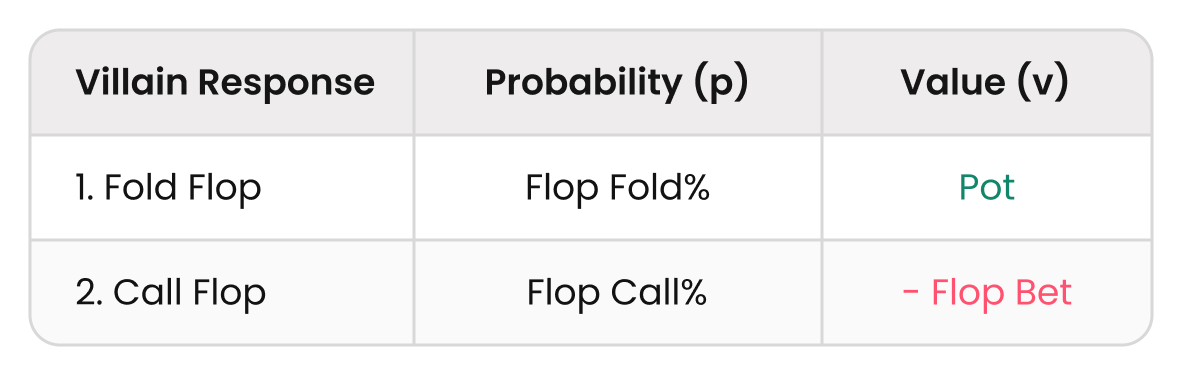
EV (Bet → Check) = Flop Fold% (Pot) + Flop Call% (-Flop Bet)
Strategy (3) Bet → Bet → Check
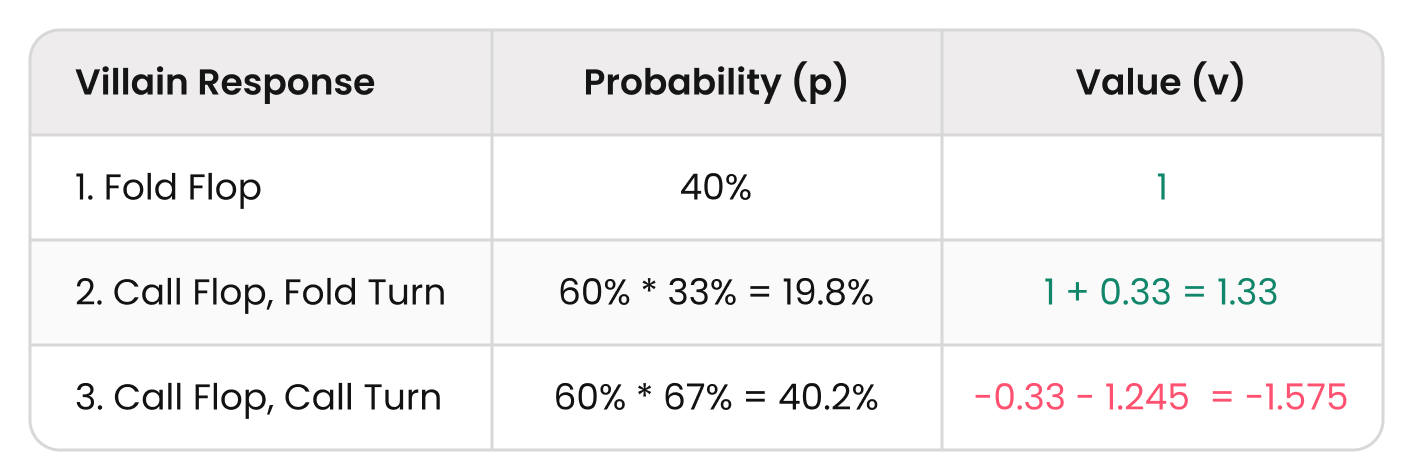
The expected value of (3)—betting twice with the intention of giving up on the river—is a bit more complicated. There are three possible outcomes.
If they immediately fold, you win the pot. If they call flop and fold turn, then you win the pot plus their flop call. If they call twice then you lose your flop and turn bets.
EV (Bet → Bet → Check) = p₁v₁ + p₂v₂ + p₃v₃
Written out explicitly:
EV (Bet → Bet → Check) = (Flop Fold%) (Pot) + (Flop Call% Turn Fold%) (Pot + Flop Bet) + (Flop Call% Turn Call%) (-Flop Bet – Turn Bet)
Strategy (4) Bet → Bet → Bet
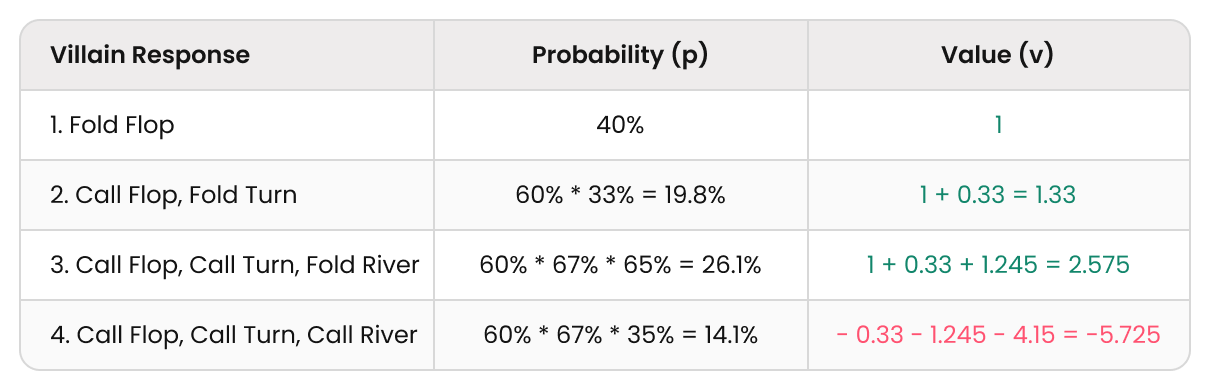
Lastly, we examine the triple-barrel strategy, which entails four possible outcomes:
EV (Bet → Bet → Bet) = p₁v₁ + p₂v₂ + p₃v₃ + p₄v₄
Spreadsheet Calculator
As you can see, this is a long and tedious calculation. It’s not difficult, just monotonous. This is the kind of work spreadsheets were made for. Here you can access my free spreadsheet calculator:
The tool is simple to use; just plug in the bet sizes and fold% for each street. The calculator will show you the EV of each strategy (under the aforementioned assumptions).
Example
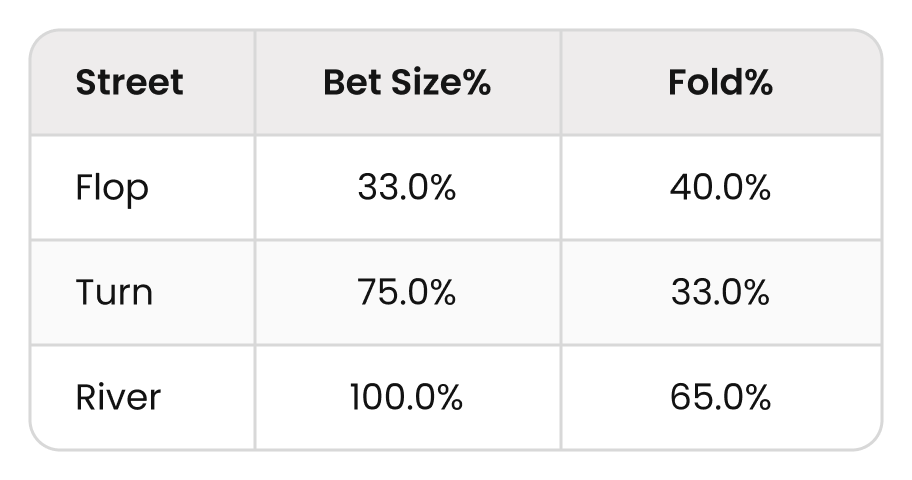
You have a pure bluff on the flop. You’re up against the type of villain that over-folds flop, then over-defends the turn, then plays scared money on the river.
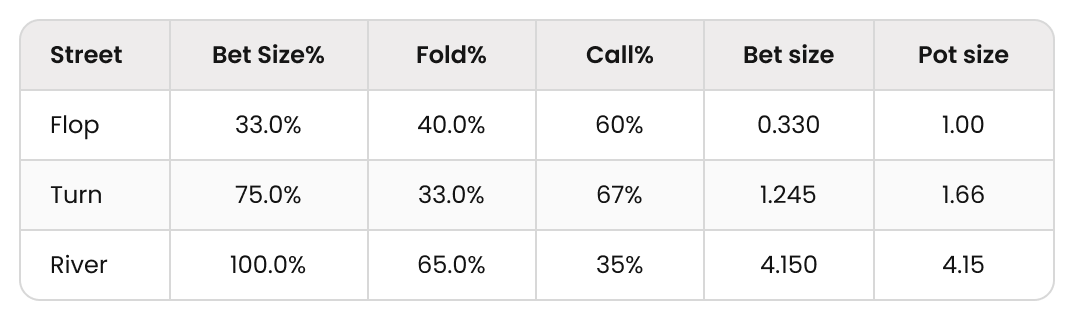
As instructed earlier, we plug in the bet sizes and fold percentages:
The first step is to convert these bet sizes from a percentage into chips. This is important because as the pot grows, we risk more for the same bet percentage. We need to compare “apples to apples” or “chips to chips” in this case. For simplicity, we will use a starting pot of 1 chip.
Step two is then to calculate the EV of each strategy:
Strategy (1) Check
Give up instantly.
EV = 0
Strategy (2) Bet → Check
Bet once, then give up.
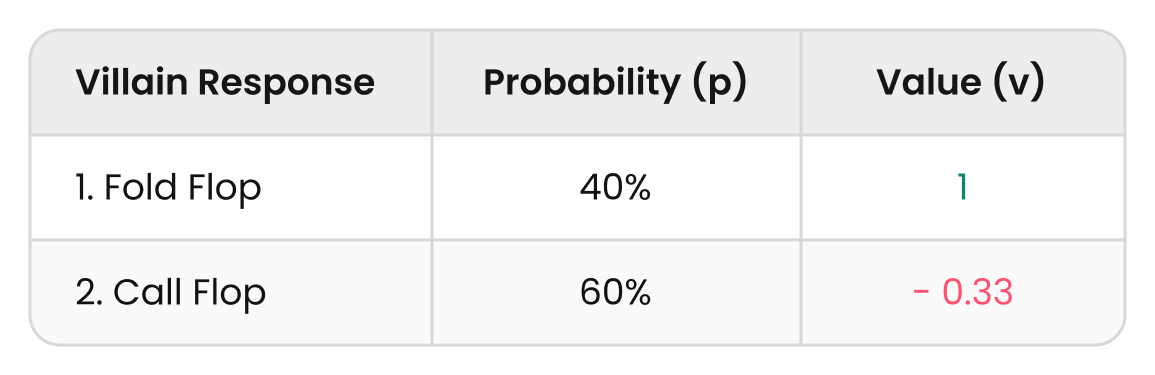
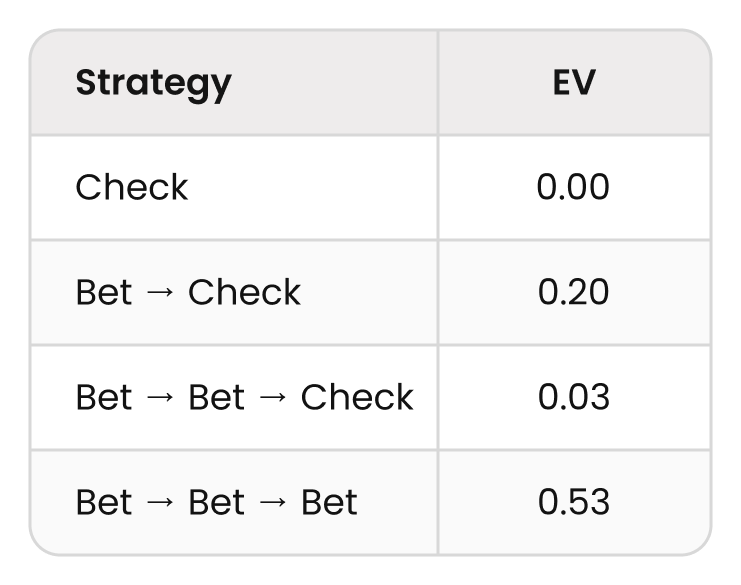
EV (Bet → Check) = p₁v₁ + p₂v₂ = 0.4 – 0.2 = 0.2
The expected value of betting once is 0.2 starting pots.
Strategy (3) Bet → Bet → Check
Bet twice, then give up.
EV (Bet → Bet → Check) = p₁v₁ + p₂v₂ + p₃v₃ = 0.4 + 0.263 – 0.633 = 0.03
The expected value of betting twice is 0.03 starting pots.
Note that our EV has dropped compared to the previous strategy. Villain is over-defending against the turn bet, so we lose most of the fold equity gained from the flop. We gained 0.4 pots in fold equity on the flop, then lost 0.37 by barreling again on the turn.
Strategy (4) Bet → Bet → Bet
Triple-barrel without giving up. No retreat, no surrender.
EV (Bet → Bet → Bet) = p₁v₁ + p₂v₂ + p₃v₃ + p₄v₄ = 0.4 + 0.263 + 0.672 – 0.807 = 0.528
The expected value of betting thrice is 0.53 starting pots. This is the most profitable strategy we have found!
Even though the turn barrel was unprofitable, we more than made up for it by betting again on the river.
The third and final step is to compare the strategies (based on the calculated EVs).
Again, note that these EV values are in “starting pots,” which we set to 1 chip. If the starting pot were 10 chips (or bb, or dollars), then you would multiply each of those figures by 10.
What About Bet → Check → Bet?
So far, we’ve assumed that we always give up if we check. But that’s not necessarily true. In our example, villain is over-defending turns but over-folding rivers. So why not just check turn?
Let’s add a new strategy to our roster:
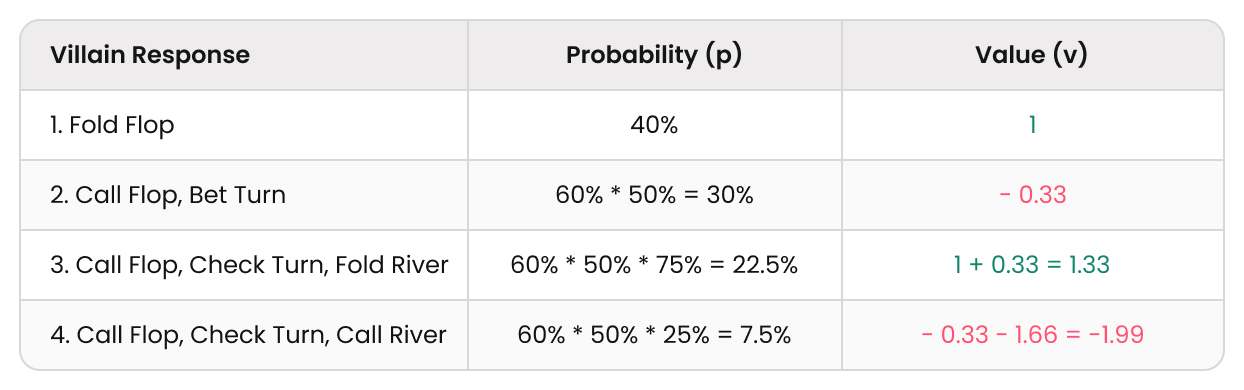
Strategy (5) Bet → Check → Bet
- Let’s assume that villain will bet 50% of the time if we check to them on the turn, with a value-heavy range that we always fold to.
- Furthermore, we’ll assume that they fold 75% of the time if we pot the river after they check behind on the turn. In this case, we are betting 1.66 chips into a pot of 1.66 on the river.
EV (Bet → Check → Bet) = p₁v₁ + p₂v₂ + p₃v₃ + p₄v₄ = 0.4 – 0.099 + 0.299 – 0.149 = 0.451
The expected value of betting twice (with an interruption on the turn) is 0.45 starting pots. Even though it seemed promising, it’s not as good as triple-barreling.
Summary
Most poker theory content stops short at the math behind a single-street bluff. However, this calculation fails when looking at multi-street bluffs. Many coaches will say something along the lines of “population over-folds rivers, so try and steer them into these lines.” But a profitable river bluff doesn’t necessarily make up for unprofitable flop and turn bluffs. This is why multi-street calculations are essential for any kind of population data analysis. If you’re looking for lines where your player pool over-folds, you can’t just look at each street in a vacuum. You need to calculate the EV of the entire line to find +EV bluffs.
The mathematics of multi-street bluff EV calculations is not difficult, but it’s tedious. While there is value in going through examples manually, in practice, you’re better off using a calculator so you can run many spots quickly and efficiently.
Even without doing mass data analysis, there are still some key takeaways to be aware of:
- Multi-street bluffs tend to offer a worse risk-reward ratio than single-street bluffs. The risk tends to outpace the reward as the pot grows each street.
- Having a profitable river bluff isn’t a license to triple-barrel everything. The EV of your river bluff needs to compensate for any negative EV on flop and/or turn, for the entire line to be profitable.
- When doing any sort of EV calculation, it is wise to break down all strategies and all outcomes of those strategies. Rather than creating lengthy formulas that encompass everything at once, break it down into a table, as shown above.
- Clearly, there is a limit to what you can do at the table during a live game. Multi-street bluff calculations should be done off-table when doing exploitative analysis.
- Sometimes, the most obvious line ≠ the most profitable line.
The BB’s incentives for calling an SB preflop raise differ from those of a cold-caller facing a raise from, say, LJ or CO. And the SB’s incentives for raising differ from those of an open-raiser in any other position.
Author
Tombos21
Tom is a long time poker theory enthusiast, GTO Wizard coach and YouTuber, and author of the Daily Dose of GTO.
Wizards, you don’t want to miss out on ‘Daily Dose of GTO,’ it’s the most valuable freeroll of the year!
We Are Hiring
We are looking for remarkable individuals to join us in our quest to build the next-generation poker training ecosystem. If you are passionate, dedicated, and driven to excel, we want to hear from you. Join us in redefining how poker is being studied.