Does your range affect your strategy?

Advanced players will often tell you that your range affects your strategy. They’ll tell you that you’re playing range-vs-range, and that you need to think about your overall range rather than only looking at your hand.

While this is undoubtedly good advice, it leads to a widespread misconception about the nature of poker. So, at the end of this article, you may look at poker strategy in a new light.

Fixed vs Dynamic Strategies

Firstly, we need to understand the difference between fixed and dynamic strategies.

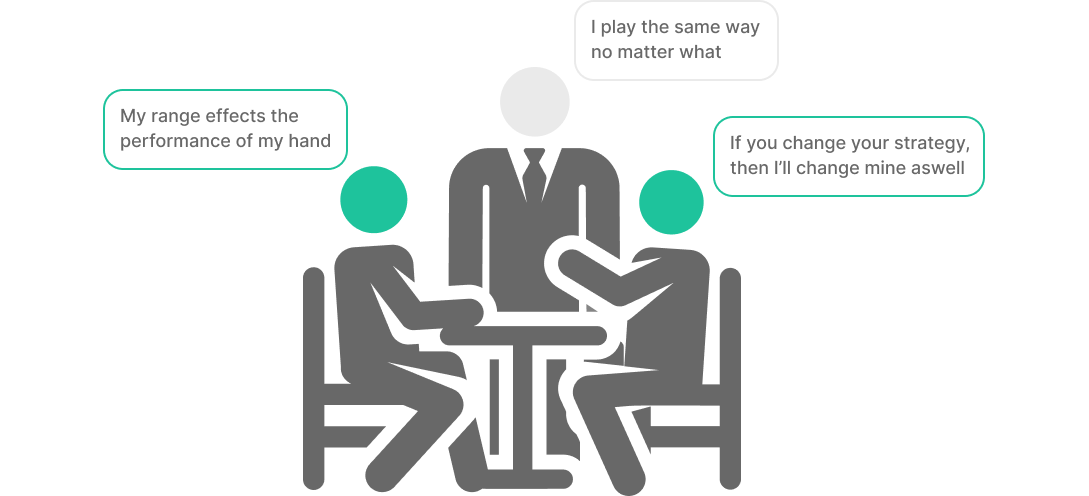
A dynamic strategy adjusts to its opponent. Therefore, a dynamic strategy can change over time. Exploitative strategies are dynamic.

A fixed strategy will not adjust to its opponent. It simply plays the same strategy no matter what. GTO is a fixed strategy, always playing its range the same way given the same spot.

This distinction is important because it tells us about the nature of indifference, GTO, and exploitative poker.

Mixing mistakes vs pure mistakes

There are fundamentally two different kinds of mistakes in poker:

Mixing mistake – Only loses EV if the opponent adjusts.

Incorrect frequencies.
Exploitable by an adaptive opponent.
NOT punished by fixed strategies.

Pure mistake– Lose EV even if the opponent doesn’t adjust.

Taking an action that strictly loses EV against the opponent’s strategy.
Loses even if the opponent doesn’t change their strategy.

GTO strategies gain when your opponents make pure mistakes. However, GTO, a fixed strategy, does not adapt to gain from its opponent’s mixing/frequency errors.

When a hand mixes between actions, e.g. raise or call, those actions should theoretically always have the same expected value (against the GTO strategy). This is the definition of indifference. Therefore, changing the frequency of mixed decisions shouldn’t effect your return – so long as your opponent’s strategy stays the same.

The calling station experiment

Two GTO bots play a HU match (no rake).

Bot 1 – Always plays a precise fixed GTO strategy.
Bot 2 – Also plays GTO, except they always CALL any hand that’s indifferent between calling and some other action.

Which bot has the edge?

Click here to see the answer

The answer is neither! The calling station bot is calling indifferent, it’s not making any “pure mistakes”. Bot 1 is playing a fixed strategy, and will not adjust to exploit it. Bot 2 is exploitable to value-heavy strategies but doesn’t lose EV because Bot 1 never adjusts. That’s the nature of equilibrium.

You can replace the calling station bot with one that always raises any hand that’s indifferent between raising and any other action. We can call this the maniac bot. Maniac Bot, who’s only ever making “mixing mistakes” and never makes pure mistakes, will not lose or gain anything against the GTO strategy.

The same goes for Nit Bot – a bot that plays GTO but always folds any hand that’s indifferent between folding and some other action. Nit Bot won’t lose anything against the fixed GTO strategy either, as GTO won’t adapt to punish the nit.

Polar toy game experiment

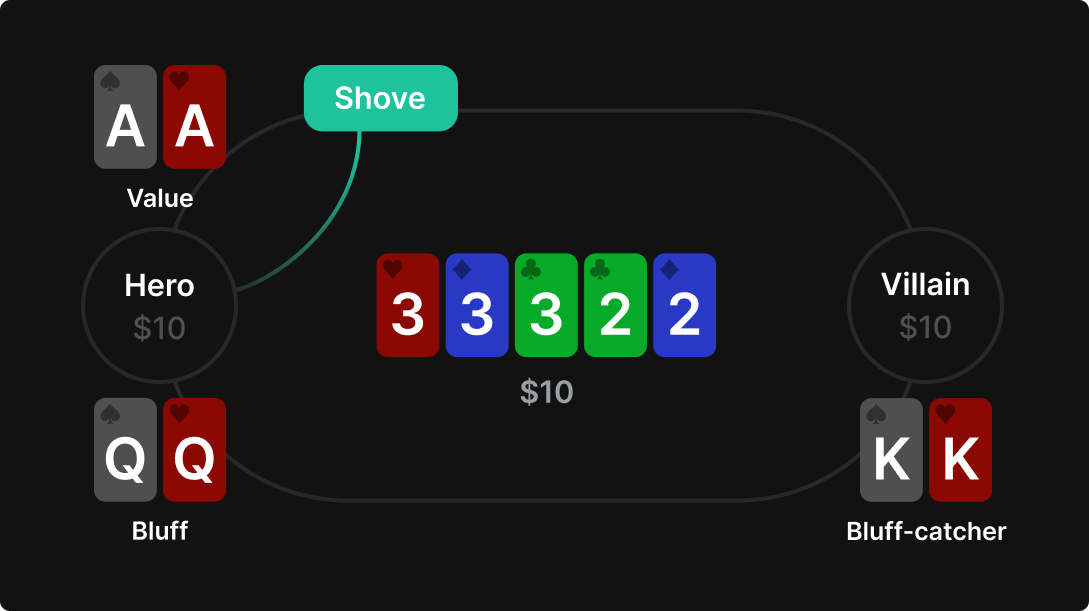
Let’s examine a clairvoyant toy game.

Pot = $10
Stack = $10
Board = 33322

Hero has: 50% AA and 50% QQ
Villain has 100% KK
Hero shoves pot on the river

Let’s start by solving this game to find the equilibrium strategy. Then we’ll adjust the strategies to see how much either player gains or loses.

Hero should always bet the nuts, and bluff enough such that villain is indifferent between calling and folding. Since we lay 2:1 with a pot-sized bet, we should give villain 33.3% equity. If we bet all of our AA, and half of our QQ, we end up with a value:bluff ratio of ⅔ value and ⅓ bluff.

Villain is indifferent facing this shove. If we were too value-heavy, they’d always fold. If we were too bluff-heavy, they’d always call. But they have precisely the right Pot Odds to call. Therefore, they should respond by calling according to the Minimum Defence Frequency.

KK should call exactly half the time facing this pot-sized bet to avoid becoming exploitable to bluff-heavy or value-heavy strategies. This has the effect of making our bluffs indifferent between betting and checking.

AA – Always shove
QQ – Shove 50%, Check 50%
Goal: Give villain 33% equity to make them indifferent between calling/folding

KK – Call 50%
Goal: Make hero’s bluffs indifferent between betting and checking.

Expected value:

Hero: $7.5
Villain: $2.5 (Hero checks back 25% of their range and always loses, so villain gains $2.5)

Quiz 1

Let’s imagine hero ALWAYS uses the equilibrium strategy outlined above. What is the expected value in these scenarios:

Villain always folds
Villain always calls

Quiz 2

Let’s imagine villain ALWAYS uses the equilibrium strategy outlined above. What is the expected value in these scenarios:

Hero always bluffs (100% AA and QQ)
Hero never bluffs (100% AA, 0% QQ)

Take a moment to try and calculate the expected value for each scenario.

Click here to see the answers

The EV in all four scenarios doesn’t change! IP’s EV is $7.5, OOP’s EV is $2.5.
Even though each player is exploitable and making huge mistakes, neither is adjusting to exploit the other because they are using fixed strategies.

Does your range affect your strategy?

This is a point that even many high-level players do not understand:

How can this be? Well, it comes down to very fundamental logic. The expected value with any hand/action is a function of your opponent’s strategy. If their strategy doesn’t change, then you aren’t playing “range vs range”, you’re playing “your hand vs their strategy” in a vacuum.

When someone says, “your range affects your optimal strategy”, there’s a hidden assumption. They’re saying that your range influences your opponent’s strategy, and if you change your range, they can change their strategy, which changes the EV of your hand in consequence.

Realistically, you’re always trying to maximize your hand vs their strategy. The reason you consider your own range is because your perceived range impacts their strategy. If they perceive you as a nit, then they stop paying off your value bets. If they perceive you as bluffy, then they call more. If they perceive your range as weak, then they can attack more aggressively.

However, if their strategy is unchanging (fixed), your range has no impact on the optimal strategy of your hand. You can simply maximize your hand against their fixed strategy without regard for balance or their perception of your range.

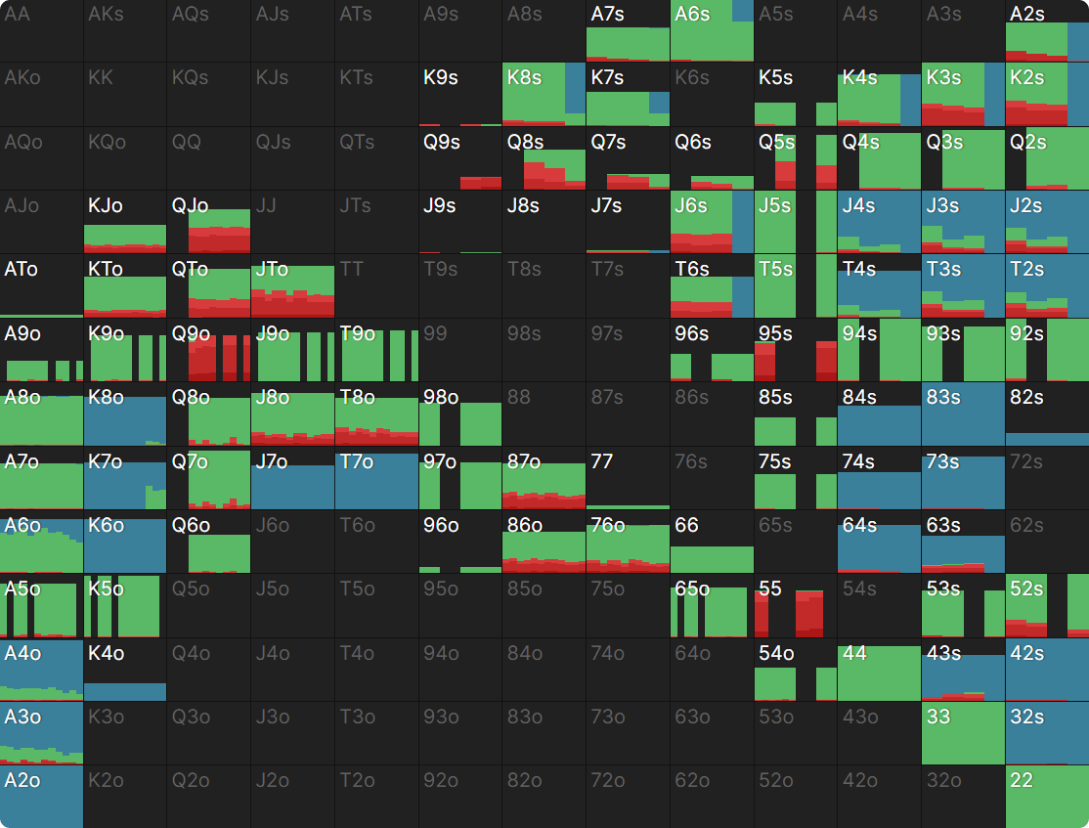
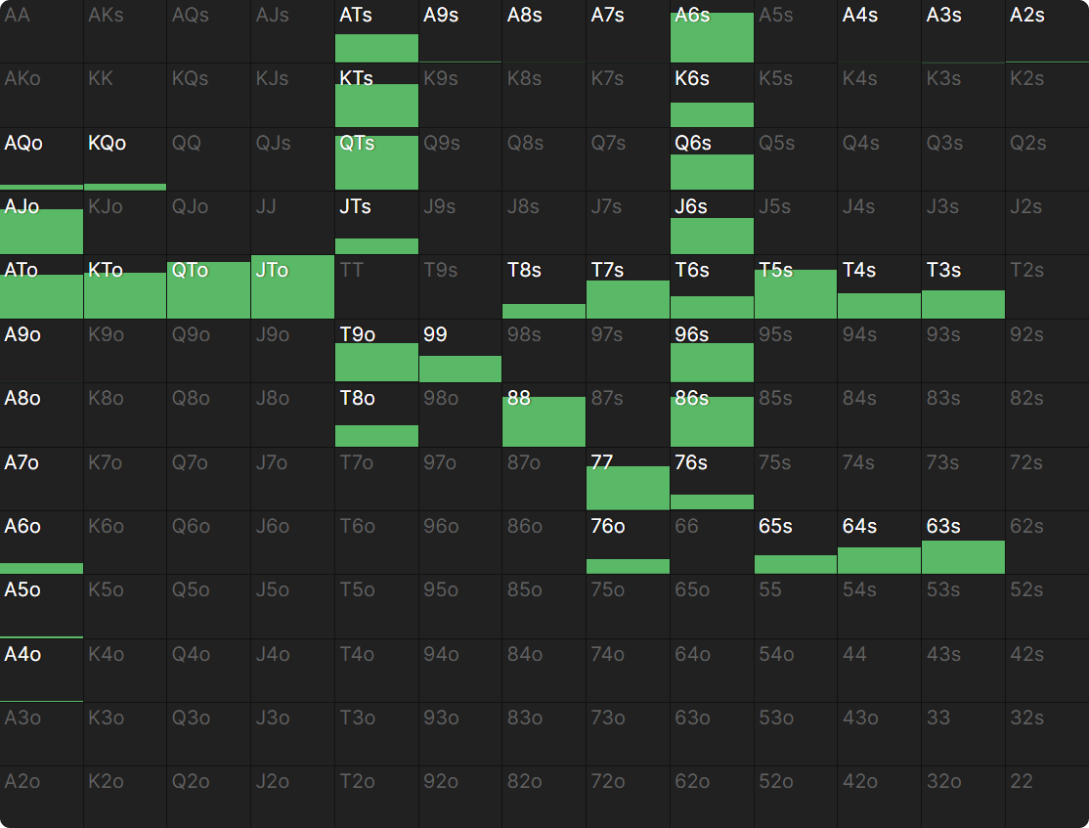
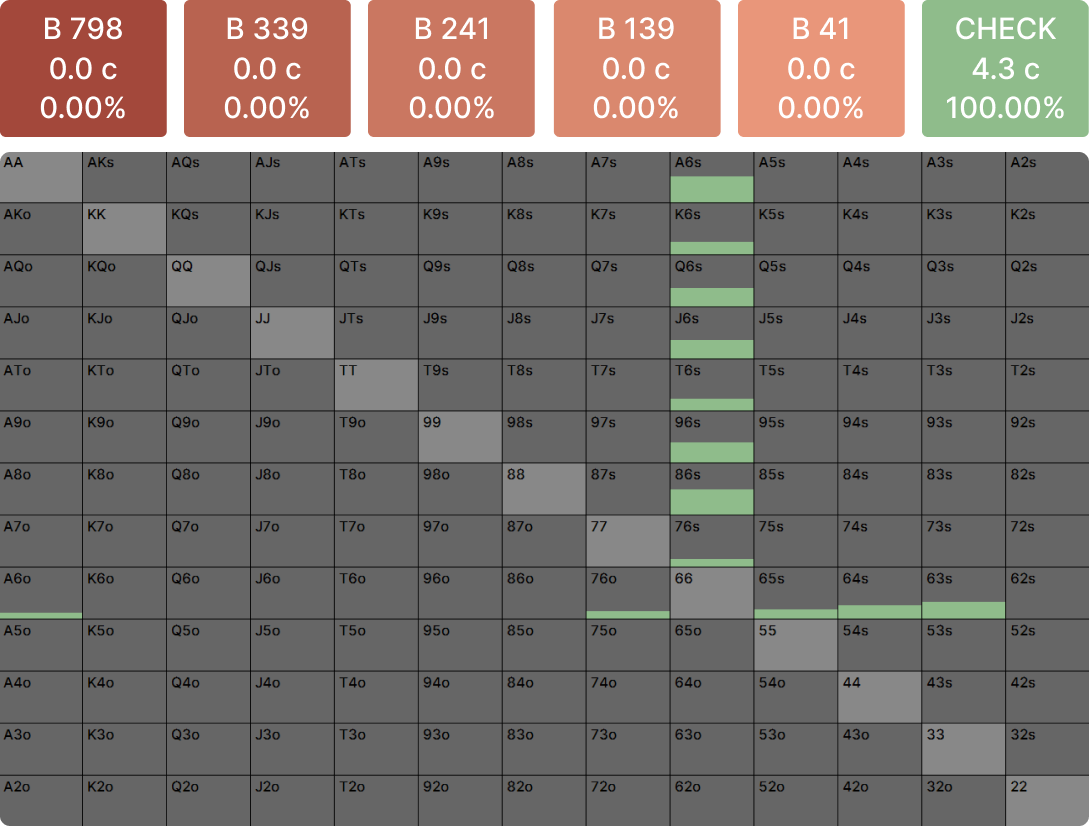
Let’s play a GTO bot

We’re playing a HU match in the BB. The bot bets 33% on Q95r:

The GTO strategy facing this bet looks like this:

The bot is playing a fixed strategy. That means we could:

Pure raise any hand that’s raised at any frequency
Call any hand that’s called at any frequency
Fold any hand that’s folded at any frequency

These actions are indifferent, and the bot won’t adapt to exploit our mixing imbalances. This is because a fixed strategy like GTO doesn’t punish mixing mistakes, only pure mistakes.

This toy game will make you angry

Let’s take a look at a BTN vs BB SRP on this T666J:

BTN bets 33% on the flop, overbets 175% on the turn, action on BB on the river.

Here BB’s best strategy is to rangecheck, regardless of hand strength.

Even the nuts should pure check. Here we see the expected value of various actions with Q6s (Quads). As you can see, checking is by far the highest EV action:

This is because our range is weak enough that villain should put in a ton of money when checked to. So quads maximize value by rangechecking.

What would happen if BB got to this river with ONLY quads, nothing else in range?
How should quads play if villain (BTN) will continue to use the same fixed strategy? Should we start leading now that our range is so nutted?

A. Should BB start betting?
B. Should they mix bets and checks?
C. Or should they continue to rangecheck?

Click here to see the answer

C. BB should continue to rangecheck!

BTN is nodelocked to use the exact same fixed GTO strategy on the river. Since checking was optimal before, it’s optimal here, despite our range being comprised of the pure nuts.

In other words, we can simply maximize each hand in a vacuum against their fixed strategy. Our own range has no impact on the best move because villain isn’t capable of adapting their strategy.

What to take away

The three most important takeaways:

Understand the difference between mixing mistakes and pure mistakes
Learn how each of these mistakes is punished
Why it’s important to distinguish between fixed and dynamic strategies

Mixed (indifferent) hands are only mixed to prevent your opponents from exploiting you. If your opponents are incapable, unable, or unwilling to adjust, then you shouldn’t be concerned with balancing mixed decisions. Instead, you should focus on maximally exploiting your opponent.

It’s important to realize that exact frequencies are less important than overall strategies. So in the Q95r example, it doesn’t matter that J3s is mixing some percentage of folds/calls/raises, what actually matters (in terms of exploitability) is how hero constructs their overall fold/call/raise ranges.

Any mixed action is playable in a vacuum. Any low-frequency play can be justified in a vacuum. You could get 100% accuracy in the hand history Analyzer and still be highly exploitable due to mixing mistakes. Conversely, you could be playing many mixing mistakes and never be exploited by the fixed GTO solution.

Instead of focusing on the minutiae of exact frequencies, take a step back and focus on the bigger picture. Look for thresholds. Use the Rangebuilder to practice constructing your entire range. Focus on thresholds, and try to answer questions like “what’s the weakest hand I bet for value?” or “What’s the strongest hand I fold against this bet size?”. Focus on indifference thresholds rather than indifferent actions! These questions sculpt your strategy and define the difference between pure mistakes and indifferent decisions.