Mathematical Misconceptions

in Poker

Pot Odds and MDF are foundational mathematical formulas in poker. This article will start with some common definitions and a cheat sheet, then explain how these common definitions lead to misconceptions about game theory optimal poker.

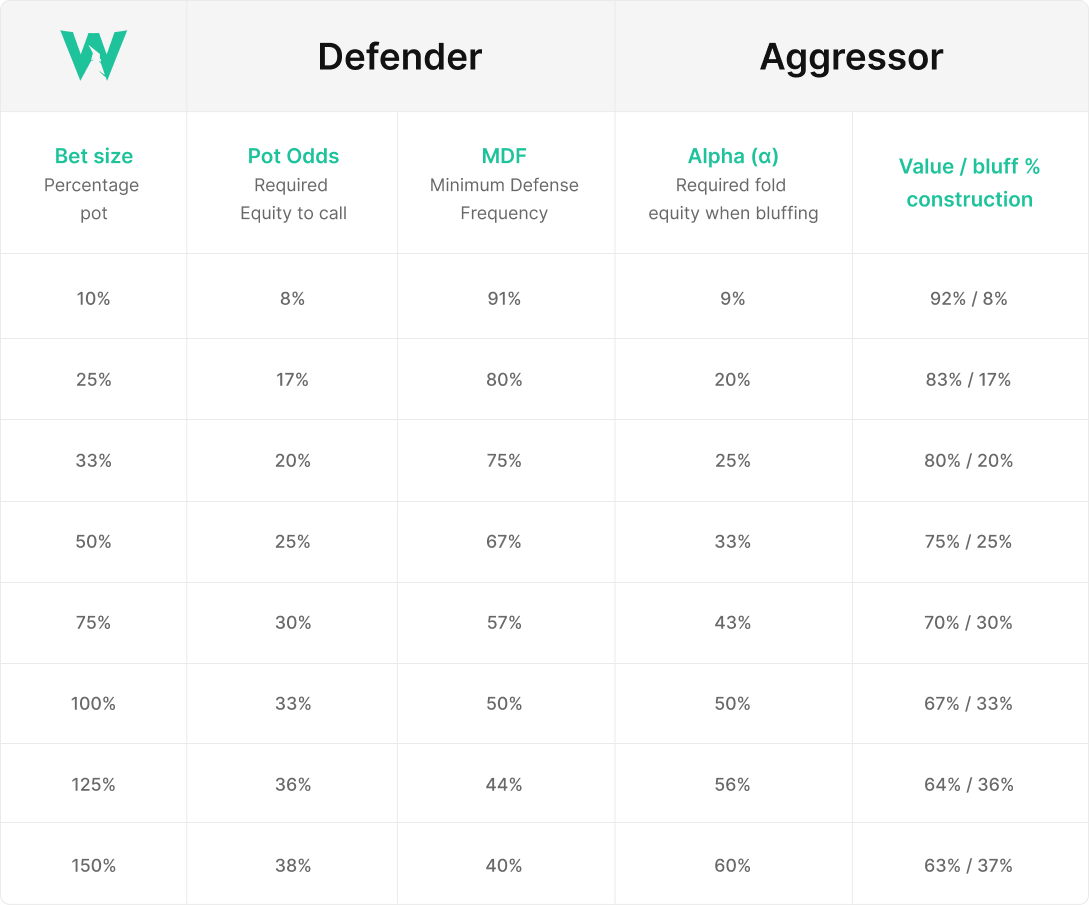
Cheat sheet

What do these mean?

***Oversimplified Definitions*** 

Pot Odds: How much equity you need to call.

Minimum Defense Frequency: How wide you need to defend.

Alpha: How often your bluffs need to work.

Value/Bluff %: How to construct your betting range.

What do these actually mean – misconceptions

How much equity you need to call.

What percentage of the pot you need to win to call. Equity does not equate to value!
For example, if your opponent bets 5bb into a 10bb pot, you must win at least 25% of the new 20bb pot (5bb) to justify calling.

Solvers often fold hands with more than enough raw equity and call hands without sufficient equity. This is because standard equity calculations assume the pot gets checked down, disregarding equity realization, position, implied odds, range advantage, and other postflop factors that affect your hand’s actual value.

How wide you need to defend.

How wide you need to defend to make your opponent’s 0% equity bluffs 0EV. This metric simply serves as a guideline to prevent others from running you over with bluffs. You don’t need to adhere to MDF if they’re clearly under-bluffing.

Furthermore, if their bluffs have value when checking back, you don’t need to defend as wide to make them indifferent between betting and checking. If their potential bluffs are worth 2 EV as a checkback, and 0EV as a bet (due to you overcalling), then they can exploit you by never bluffing.

How often your bluffs need to work.

How often your 0% equity bluffs need to work. In practice, almost everything has equity before the river. This also does not account for the fact that you can bluff multiple streets.

How to construct your betting range.

This ratio is only correct on the river, assuming all your value hands are the nuts and your bluffs are worthless. Value/bluff ratios get more complicated over many streets. A very basic guideline is to use the ⅓ ½ ⅔ rule – you need about ⅓ value on the flop, ½ value on the turn, and ⅔ value on the river. However, this depends on factors such as bet sizing and polarity. See the caveman GTO calculator to learn more.

Secondly, due to blocker effects and/or rake it’s typically advised to go slightly more value heavy than this chart indicates.

Formulas

Pot Odds = call / (pot size after you call)

Alpha = risk / (risk + reward)
Where risk and reward are the amounts risked on a bluff, and the amount gained if the bluff is successful.

Minimum Defense Frequency = 1 – alpha
When facing a bet (not a raise): MDF = 1 / (1 + bet%)

Bluff% = pot odds laid, you need to bluff this often to make your opponent indifferent on the river.
Value% = 1 – bluff%

Example 1 – Making a bet

Hero bets 5 into 10 (half-pot) on the river

Pot odds: Villain needs to call 5, and the pot will be 20 after they call.
Required equity to call = 5 / (5 + 5 + 10) = 5/20 = 25%.
Villain should call any hand that wins more than ¼ of the time at showdown.

Alpha: Hero is risking 5 to win 10

a = 5 / (5 + 10) = 33%. Villain needs to fold at least ⅓ of the time to break even on a 0% equity bluff.

MDF = 1 / (1 + ½ ) = 66%. Villain should defend at least ⅔ of their range to make bluffs indifferent.

Value/bluff ratio: Hero should bet with a range of 75% value and 25% bluffs to make villain’s bluff-catchers indifferent between calling and folding.

Example 2 – Facing a raise

Hero bets 5 into 10 (half-pot) on the river and Villain raises (half-pot) to 15:

Pot odds: Hero needs to call 10 more, and the pot will be 40 after you call.
Required equity to call = (15-5) / (10 + 15 + 15) = 10/40 = 25%.
Hero should call any hand that wins more than ¼ of the time at showdown.

Alpha: Villain is risking 15 to win 15
a = 15 / (15 + 15) = 50%. Hero needs to fold at least ½ of the time for villain to break even on a 0% equity bluff.

MDF = 1 – alpha = 50%. Hero should defend at least ½ of their range to make villain’s bluffs indifferent.

Value/bluff ratio: Villain should bet with a range of 75% value and 25% bluffs to make Hero’s bluff-catchers indifferent between calling and folding.

Spreadsheet calculators

Here’s a free tool you can use to calculate MDF/pot odds, alpha, geometric sizes, bluff/value ratios by street, and much more!

Applications in game theory vs practice

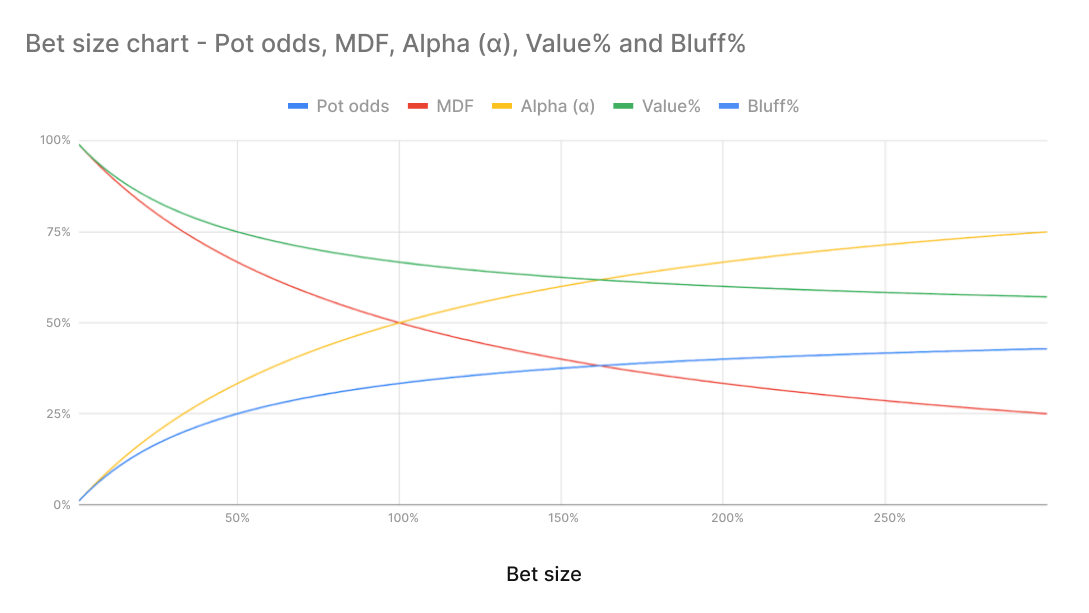
The following graph shows how these variables interact as the bet size changes. Curiously, they intersect at the Golden Ratio, a well-known mathematical constant found throughout nature.

Pot odds are the most theoretically sound metric

We can find plenty of spots on preflop-turn where solvers will fold hands with more than enough equity, or call hands without enough equity. However, pot odds are always a correct metric if we look at pot share (what percentage of the pot a hand actually expects to win, given all the postflop variables).

Even in practice, even against fishy ranges, pot odds will always be a theoretically correct metric, so long as you’re looking at your true value of the pot, rather than raw checked-down equity.

If you’re facing a pot-sized bet, then you need to win at least ⅓ of the pot, on average, to profitably call. It’s really as simple as that.

MDF and Alpha

MDF and Alpha get a bad rep for being frequently misused… These are closer to an idealized toy game metric than a hard law of poker. MDF and Alpha are based on bluffs with no equity; it’s designed to give a bluff 0EV. This is rarely the case.

At most, you only need to make their bluffs indifferent between checking and betting. If bluffs have 1bb checking, and you overdefend to make those bluffs 0EV, then your opponent can simply stop bluffing. Why should they take the lower EV action?

Many beginner players use these metrics to justify poor calls or bluffs. Always remember, MDF is a shield to prevent your opponent from overbluffing. If they’re never overbluffing, put down your shield and stop calling bluff-catchers!

In general, solvers defend much closer to MDF in position than out of position. That’s because checking back a weak hand has more value in position. Remember, you don’t need to give them a 0EV bluff, at most you only need to make their bluffs indifferent between checking and betting!

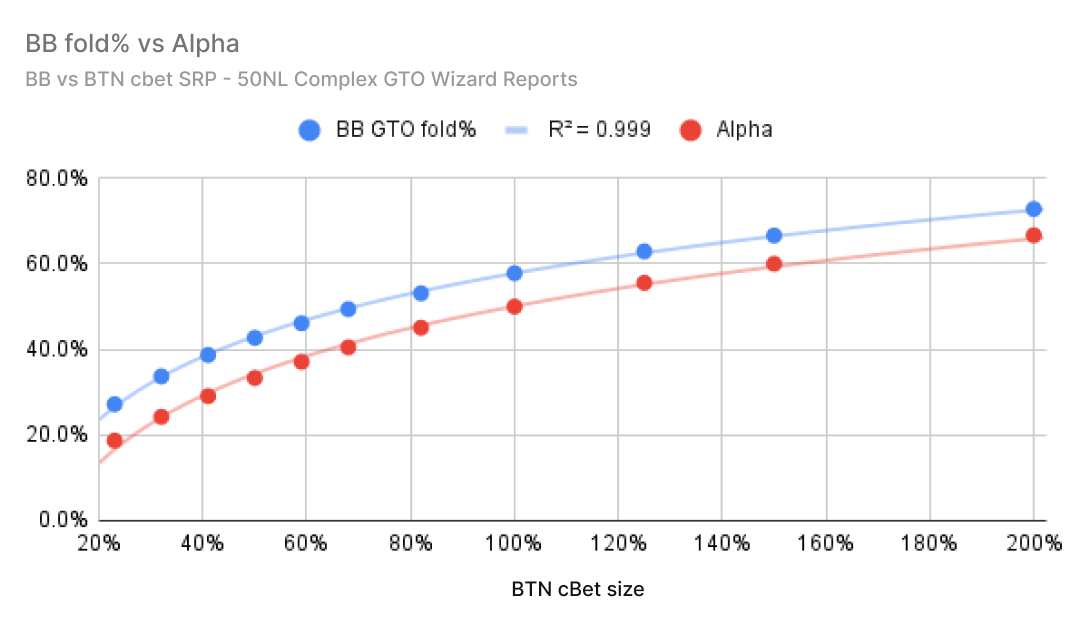
GTO Wizard offers unparalleled data analysis. Let’s compare how often the BB folds against how often MDF says they should fold, vs a BTN cbet. I’ve graphed every cbet size in the complex solution between 20% and 200%, across all 1755 strategically distinct flops.

As you can see, BB consistently overfolds (compared to MDF) against every size.

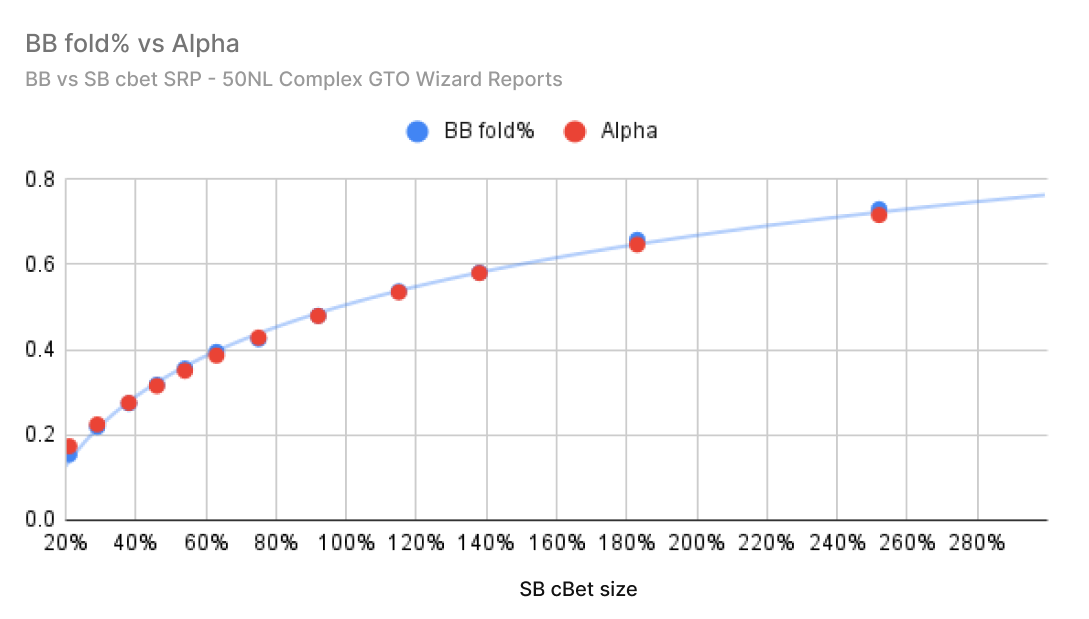
Let’s check blind vs blind. Again, BB is at range disadvantage. However, this time BB has position.

We can see the BB fold% vs a SB cbet (and how often BB “ought to be folding”). On average, the BB defends extremely close to MDF overall. Not every flop is perfectly matched, but the overall trendline matches extremely closely with MDF.

What to take away

What to take away from these charts: Defend closer to MDF in position, overfold out of position.

What to take away from MDF in general: Use this as a shield to prevent overbluffing. Do not call bluff-catchers if your opponent is obviously underbluffing!