The Right Way To Think About Protection

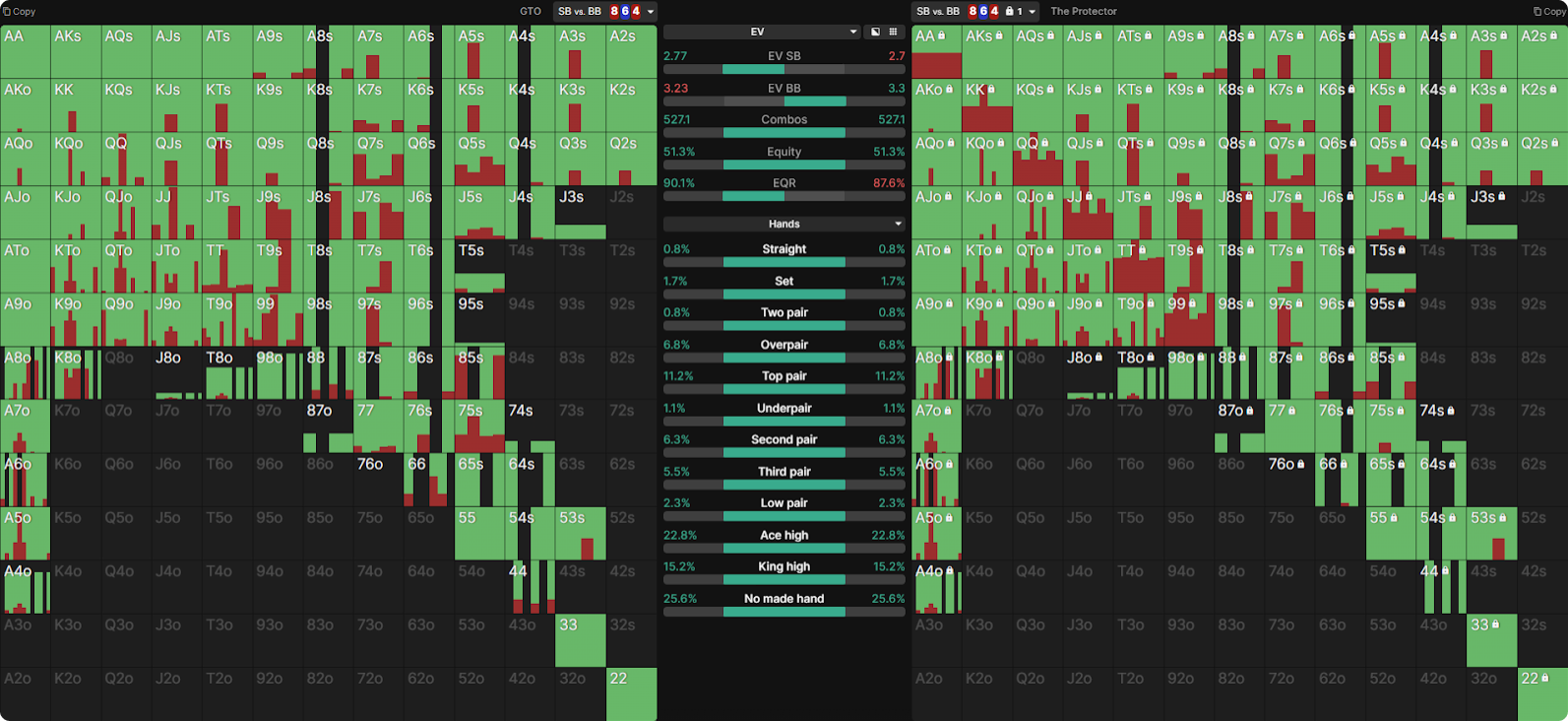
Suppose Paul the Protector is in a 200bb cash game and opens A♠A♣ in the SB. The BB calls, and the flop is 8♥6♦4♥. He might be tempted to fire a 75% pot c-bet here, as betting allows him to “charge flush draws on a wet board” and “protect his hand against some straight draws,” both of which his hand unblocks. Additionally, he might not want to allow his opponent to check behind and see a “free card,” which could be an unfavorable turn like a heart, 7, or 5. Paul might be surprised to learn, however, that this hand is close to a pure check in theory, and betting 75% pot loses him around 7% of the pot in expectation.

In this article, we will dive into this scenario and further examine when and when not to bet for protection. We’ll also discover how the concept of protection influences the frequencies and sizings associated with a flop c-bet strategy.

When Not To Protect

So where does the logic from the above situation break down? While BB does defend against Paul’s 75% bet with flush and straight draws that are behind A♠A♣ in raw equity, these draws have relatively high EV due to their implied oddsImplied odds
A calculation of odds that takes into consideration future betting, thus allowing players to estimate the additional bets they could gain on future streets should they make their hand.Reverse implied odds refer to the value lost when making a hand and losing to a stronger made hand anyway.: they can try to extract value from AA when they hit or bluff off AA when they miss. When BB continues and the runout is “scary,” Paul’s AA will often become a bluff catcherBluff catcher
A hand that is likely only able to beat the opponent’s bluffs, and will therefore likely lose to the opponent’s value hands., with zero EV in a pot that he built. When Paul the Protector bets his AA, narrowing his opponent’s range so that AA is transformed into a 0EV bluff catcher, he has effectively lost all the money he has put into the pot thus far. This is far from an ideal outcome when holding a hand with such high equity on the flop.

Unblocking continues isn’t ideal either: when Paul c-bets 4.5bb into a pot of 6bb, his expected value with A♠A♣ when called is 11.19bb. Since this number barely exceeds the starting pot size plus his c-bet size, his hand enjoys only slightly higher EV when BB calls, compared to getting a fold. Put another way, the change to AA’s EV when called (EV − Flop Contribution) is 6.69bb, whereas the change to its EV when BB folds is 6bb. Getting a fold is almost as good as getting called, highlighting how poorly this hand performs as a value bet.

There is another hidden benefit to checking: when Paul checks OOP, BB is not guaranteed to check back. Because this board texture is relatively advantageous for their range, she will stab with hands such as Q♦9♠ and K♣2♣, which are drawing near-deadDrawing dead
When one player has no outs to win a hand, and is therefore guaranteed to lose the hand if it goes to showdown. against his specific hand but are fairly trivial folds vs the 75% bet.

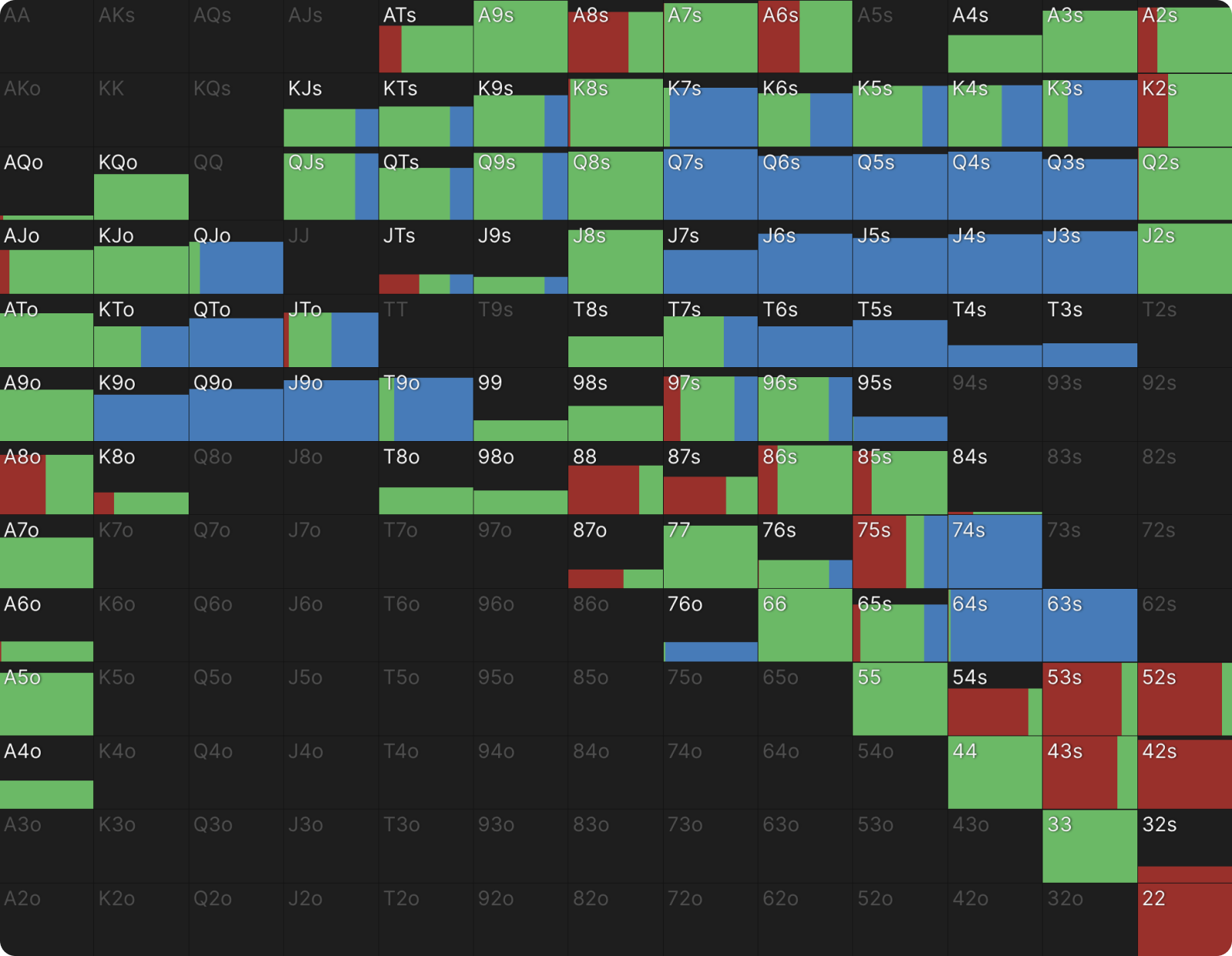
In general, a bet will obtain more value when it gets called by a hand that is drawing dead, as opposed to when it gets called by a hand that has live outs and possibly implied odds too. This explains why c-betting A♠A♣ on 8♥6♦2♣ is more acceptable. When the board is drier, BB is required to defend with more no-pair no-draw (“static-equity”) type hands, mostly overcards with backdoors. On 8♥6♦2♣, 37% of these hands continue facing a 75% c-bet, compared to 22% on 8♥6♦4♥. For AA, getting called by KQ on 862r is a much better result than getting called by 76 on 864tt.

A bet will obtain more value when it gets called by a hand that is drawing dead, as opposed to when it gets called by a hand that has live outs and possibly implied odds too.

Worrying about protection too much can come with a steep price tag. On 8♥6♦4♥, a GTO c-betting strategy captures 2.77bb in expected value from the pot. Imagine Paul c-bets too many overpairs (which “need protection”) and too few straights, sets, and pair+draws (which don’t “need protection”). If we nodelockNodelock
The act of fixing one players strategy at some node within a solver. Typically this is done to calculate exploitative adjustments. him to this strategy, we find that he captures only 2.7bb and thus is exploitable for around 0.07bb (7bb/100):

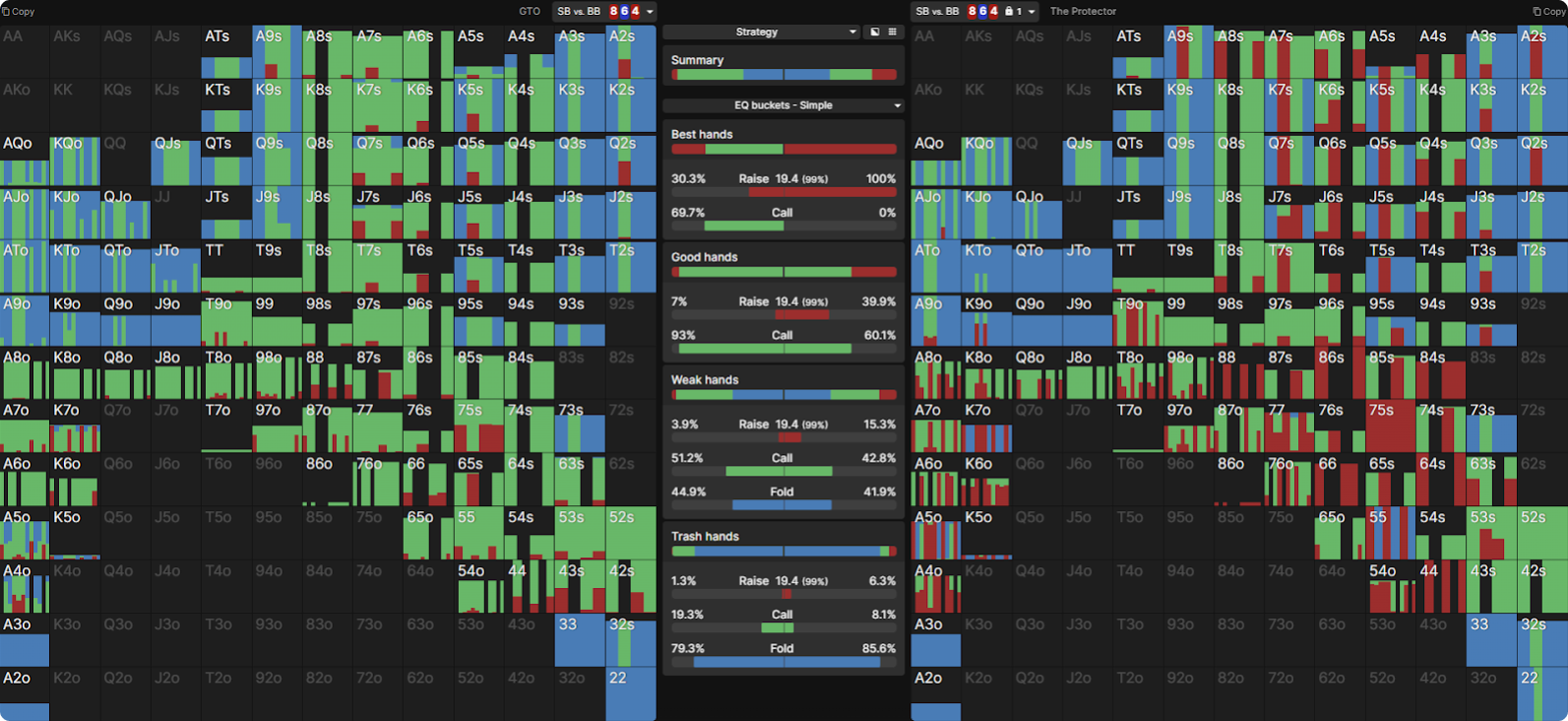
Paul’s c-betting range is relatively cappedCapped
A range without many very strong hands, relative to the board. See uncapped. and too dense in overpairs, which are too weak to happily stack off for 200bb. This vulnerability in SB’s range allows BB to pounce by ramping up their raising frequency (for a re-pot sizing) from 5% to 21%—always raising with two pair or better and adding requisite bluffs:

In fact, a far more robust strategy for Paul would be to check his entire range. He lacks the positional advantage, and BB’s range is competitive in terms of not only its overall equity but also strong hands (two pair+). This strategy captures 2.75bb in EV, which is much closer to GTO (and may outperform it, if BB over-stabs).

When To Protect

In poker, bets and raises derive EV from inducing low-equity hands to call and high-equity hands to fold. As we have established, it is imprudent to design a flop c-betting strategy with the goal of pricing in a high-equity draw. Rather, the primary goal of betting with “value hands” should be to get calls from hands that are drawing much closer to dead. On the flip side, the goal of betting with “bluffs” should be to fold out as much equity as possible.

When thin value hands can also “bluff” off/deny another part of the defender’s range (including gutshots, overcards, backdoor draws, etc.), we can bet them “for protection.”

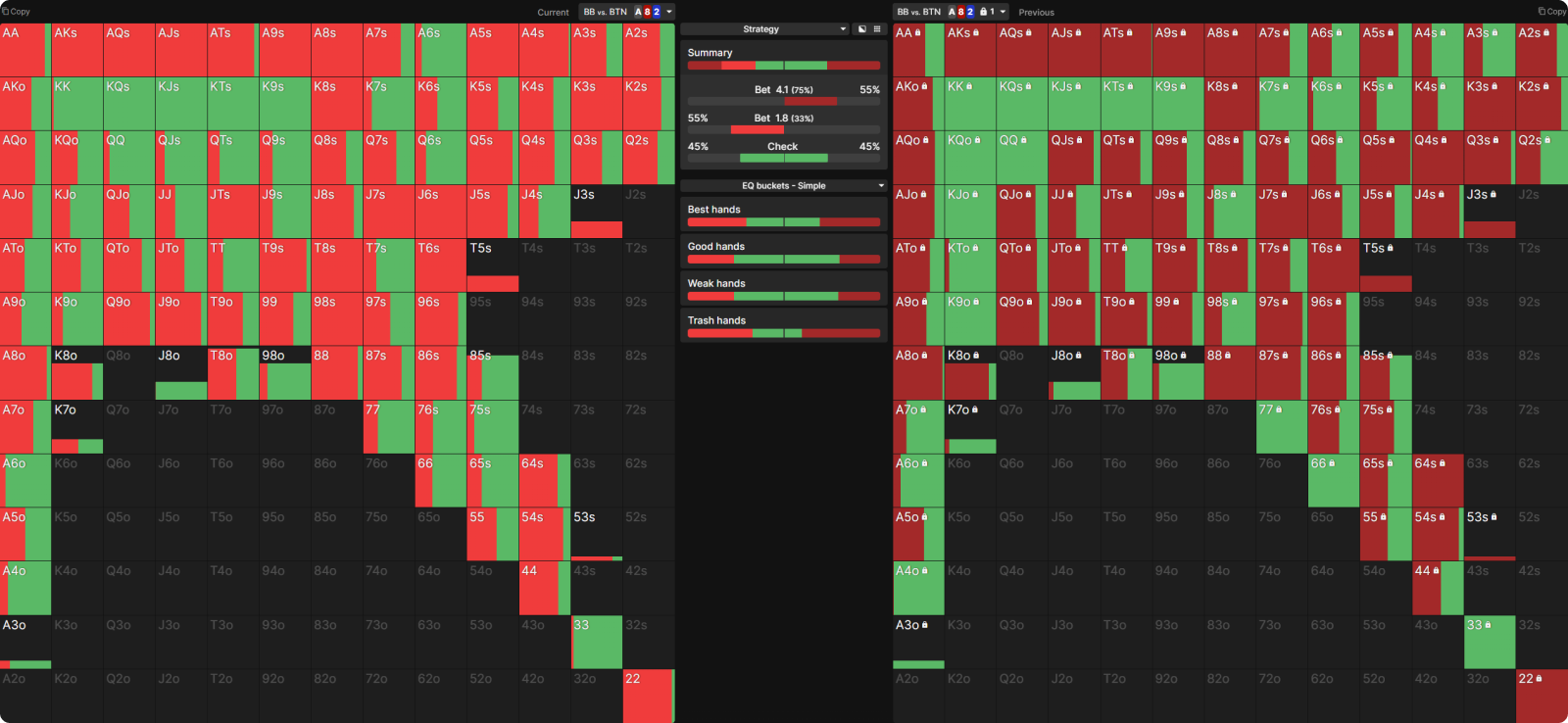
For example, consider BTN’s c-bet strategy on A82 rainbow in a single-raised pot against the BB. Note that BB continues preflop with nearly every offsuit (and suited) hand with two cards 9 or above. BB arrives at the flop with over 100 combinations of two cards between a King and Nine, accounting for nearly 30% of range. As a result, BTN is strongly incentivized to place a small wager with 8-x to fold out these hands (which have up to 6 immediate outs) and to extract value from hands like 77–33 (which have at most 2 outs):

While a large bet might fold out even more overcard hands, sizing up with 8-x would isolate it against a stronger range that’s more weighted toward Ace-x, and so it would fare poorly when called. If BTN employs a c-bet strategy with a single 33% sizing, he will be able to bet 8-x over 70% of the time. If we force BTN to use a 75% c-bet at the same frequency as the smaller sizing, they lose 6bb/100 of expected value.

When thin value has the incentive to bet for protection, smaller sizings must be used to allow these hands to bet frequently.

In the next section, we will further investigate the relationship between protection and frequencies/sizings with which the flop should be c-bet.

Frequencies and Sizings

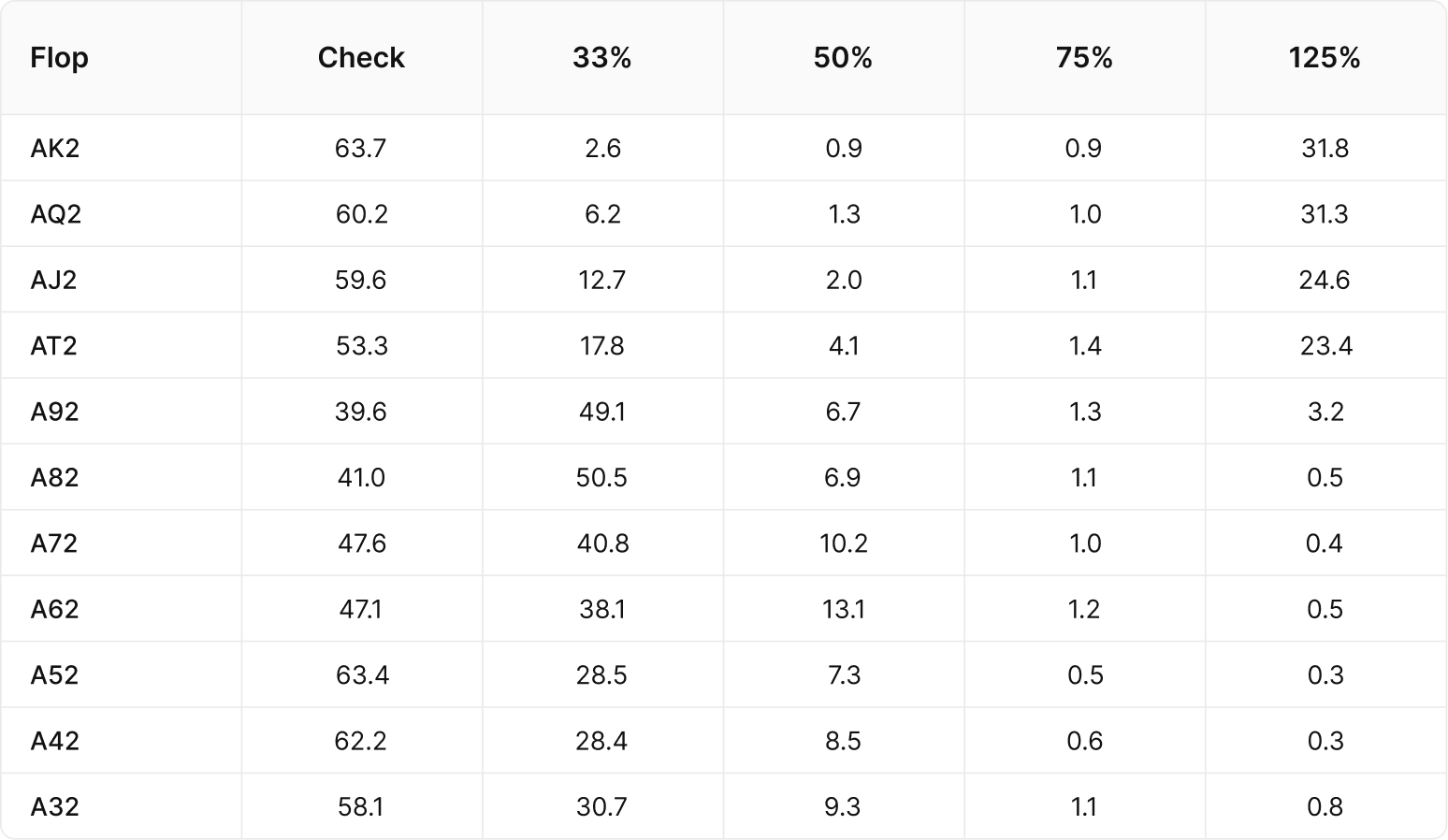
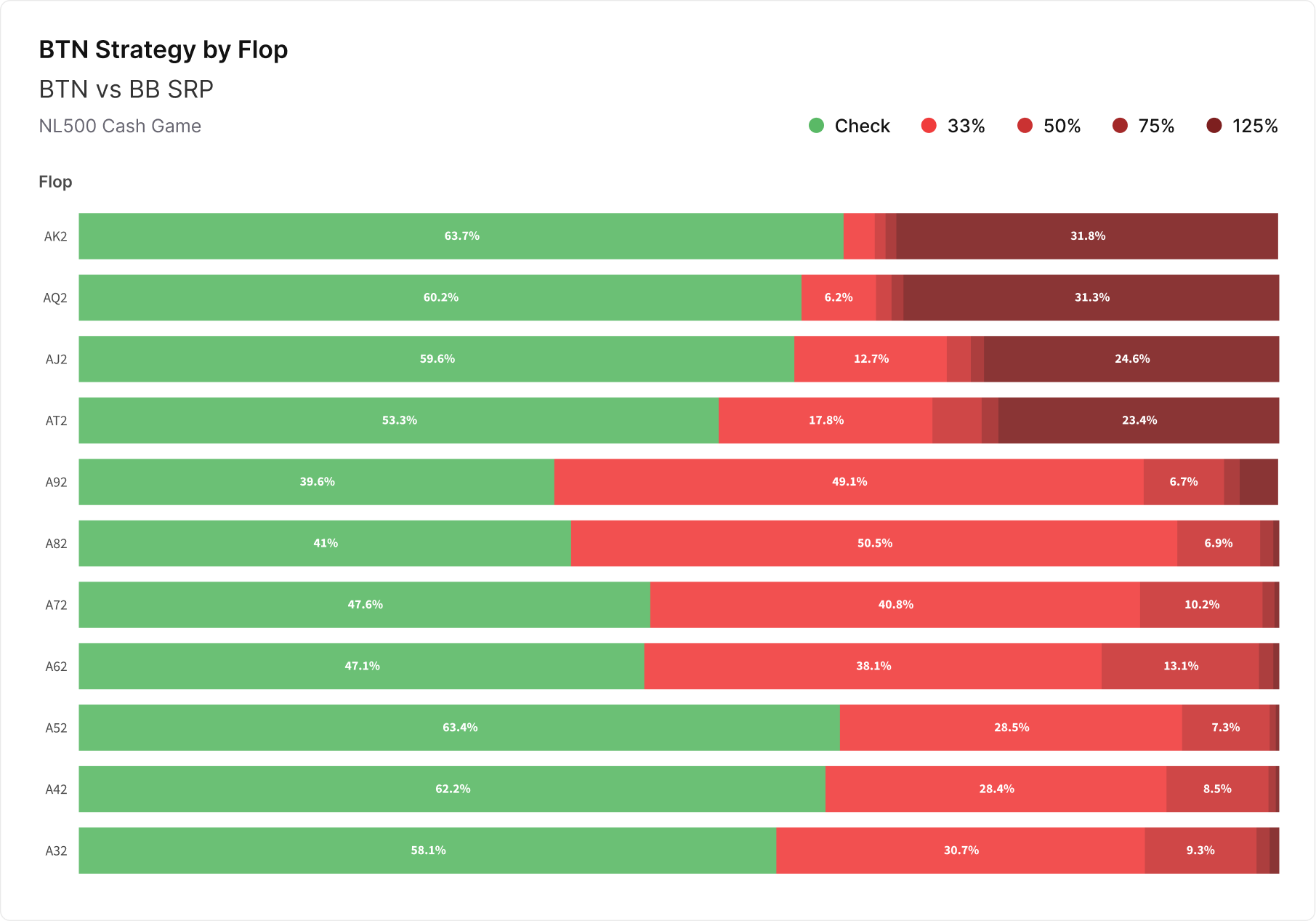
Using the Aggregate Reports feature, let’s take a look at BTN’s c-bet strategies vs the BB in a SRP, where the board is AX2 rainbow and X is a card between a K and 3:

We can observe a clear dichotomy: BTN’s primary sizing is a 125% when X is a Broadway cardBroadway
A ten through ace straight. “Broadway cards” can also be used to describe any 10, J, Q, K, or A card. and 33% otherwise. In the former case, there are fewer overcards to second pair, and the existence of Broadway gutshots (of which BB has all offsuit combinations) reduces the equity of BTN’s made hands. Consequently, BTN is reluctant to protection-bet with second pair, so BTN c-bets larger with a polarized rangePolarized
Describes a range that is mainly very strong made hands or bluffs, with very few middle strength hands. consisting of mostly good top pairs+ and bluffs. (As an added bonus, the overbet sizing makes many Broadway gutshots indifferent.) In the latter case, there are more overcards to second pair and BTN is eager to protection-bet with second pair and underpairs, so the predominant sizing decreases.

Conclusion

Strong draws on the flop have high EV (often more than many made hands) and will always continue facing most “standard” c-bet sizes. When c-betting the flop, don’t focus on “charging” these hands. Instead, think about the following heuristics:

When you are OOP and lack a significant range advantageRange advantage
A general term meaning one players range equity distribution is stronger on a given board. It’s possible to have an advantage only over a specific part of the equity distribution. A large advantage near the top of the range indicates a nut advantage., check frequently.
Hands that can make the effective nuts by the river have high EV/EQR, even compared to better made hands. (The categorization of “effective nuts” is highly dependent on stack depth.)
Bet more frequently with hands that are likely to remain value bets/raises, rather than degrade into bluff catchers, on future streets. These hands are often said to have “high equity retention” or “robust equity.”
Pay attention to offsuit hands in both ranges, as each such hand represents 12 combinations.
Pay attention to the value of fold equity. It’s not just about how often your opponent will fold, but the type of hands they fold.
If your thin value bets would fold out hands with many outs against you, then you have more incentive to go for fold equity. Consider betting small with a wide merged range.
If your thin value bets would mostly fold out dominated hands while getting called by high equity draws and better, then you have less incentive to bet thin. In these spots, you should opt for a more polarized betting strategy.
When gutshots constitute a large part of your opponent’s range, overbetting forces indifference from many of these draws.