The Value of Fold Equity – Experiment

The term “fold equity” is ambiguous in the poker community. Firstly, it’s an EV equation, not an equity equation. The classical definition of fold equity is: EV = (how often they fold x size of the pot).

However, this definition misses something obvious – fold equity is relative to your hand!

Put another way, the value gained from making your opponent fold depends on how their folding range interacts with your hand. If you only fold out hands you had dominated, did you actually gain anything?

This article will explore this concept through experimentation and measurement. The end goal is to give you a more concrete way to think about the relative value of fold equity.

We’re going to cover 3 different experiments

You can learn more about the value of fold equity in this video:

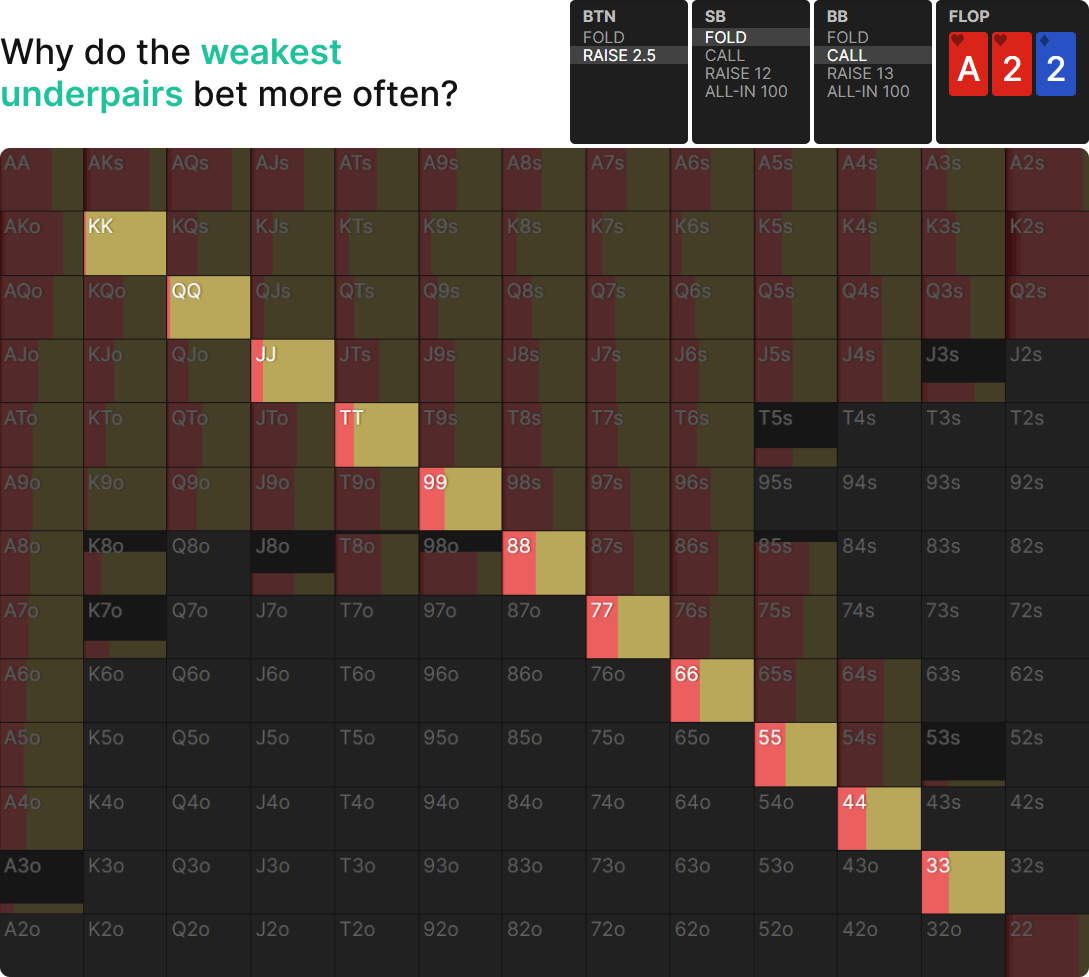
BTN open, BB call, flop is A22tt (tt = two-tone)

Why do the weakest underpairs prefer to bet more often?

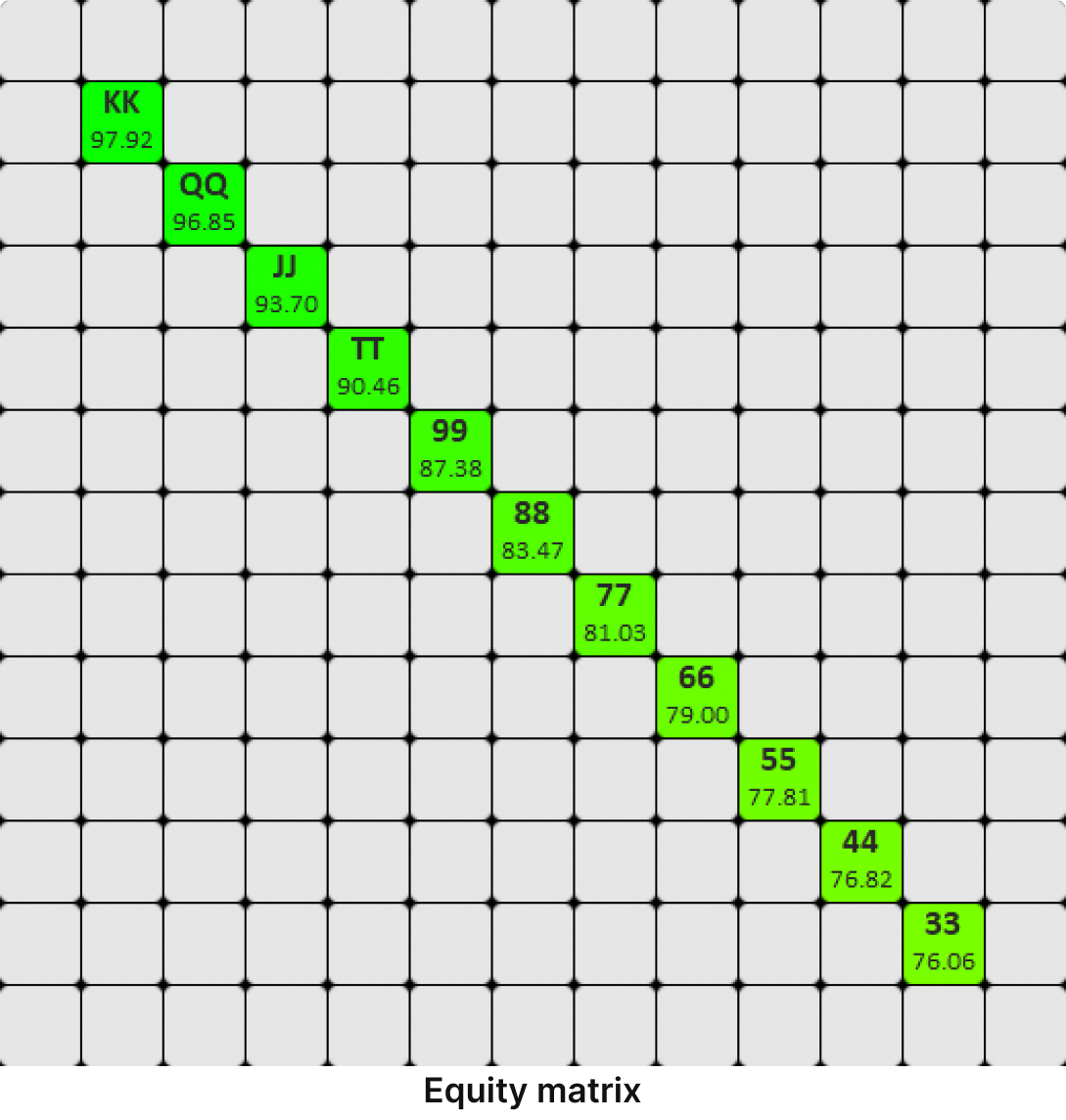
Let’s copy BB’s folding range and put that into an equity calculator. Here’s our underpair equity against their folding range:

Results: Higher underpairs do not fold out equity that can outdraw them and are less incentivized to bluff.

KK has 98% against the folding range, so the value of fold equity for this hand is nearly zero relative to checking. You only fold out hands that you have absolutely dominated. This hand is not incentivized to generate folds and can only gain by making worse hands call.

33, on the other hand, only has 76% against the folding range since we fold out so many overcards to our pair that can outdraw us later. Therefore the value of fold equity with 33 is much higher. This hand has more to gain from generating folds.

Conclusion: The value of fold equity impacts your incentive to bet. More vulnerable pocket pairs are more inclined to bet.

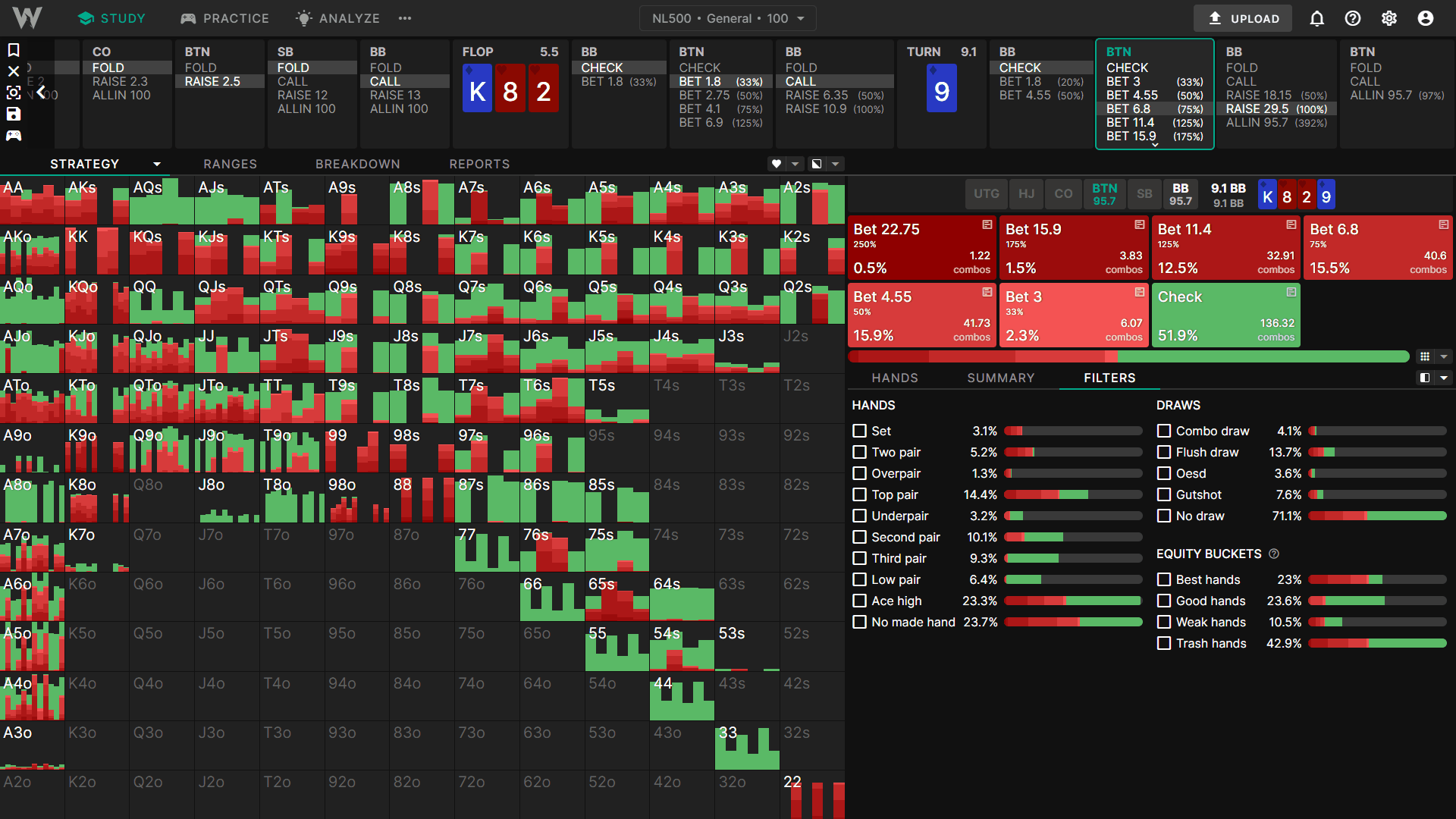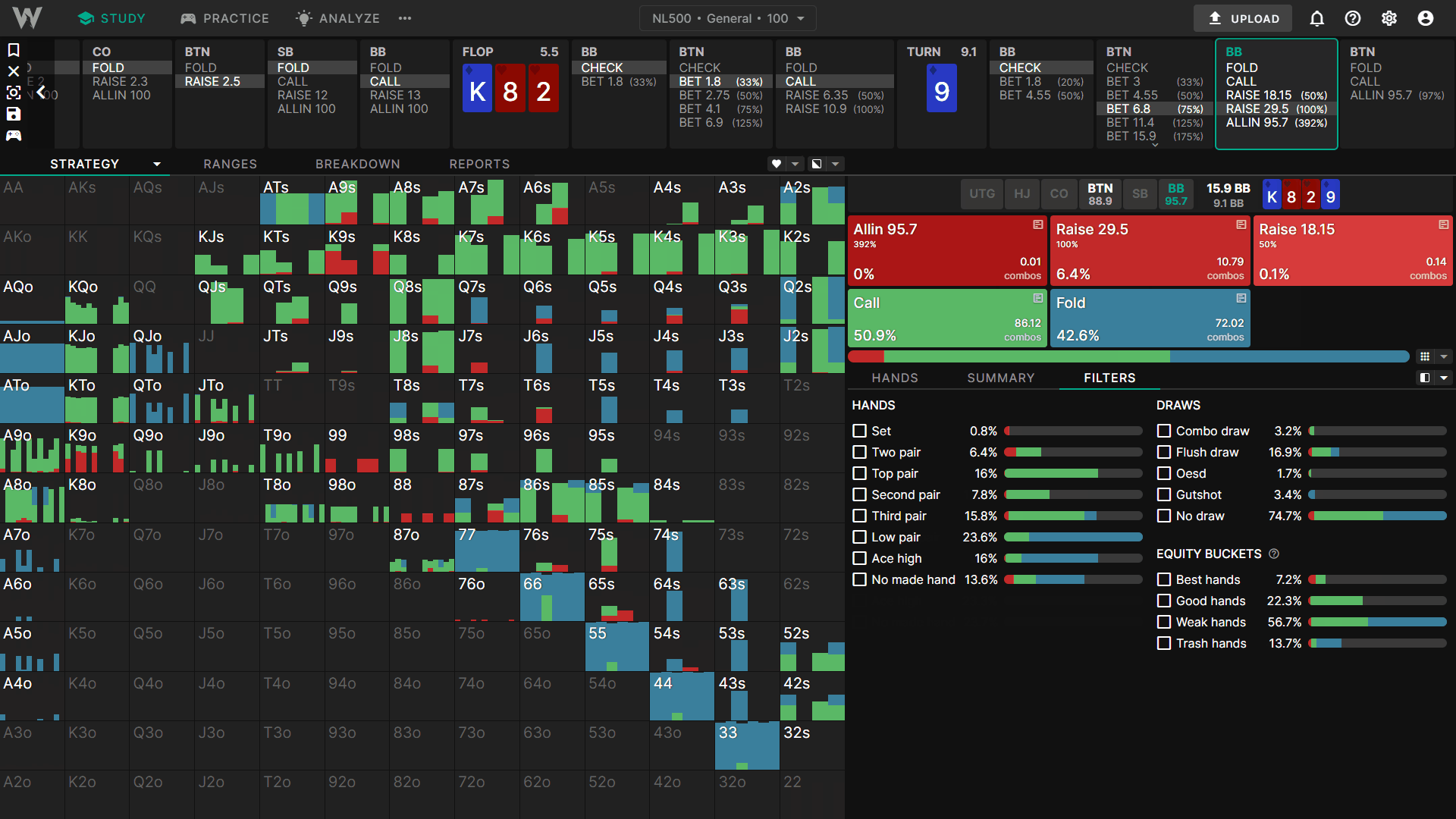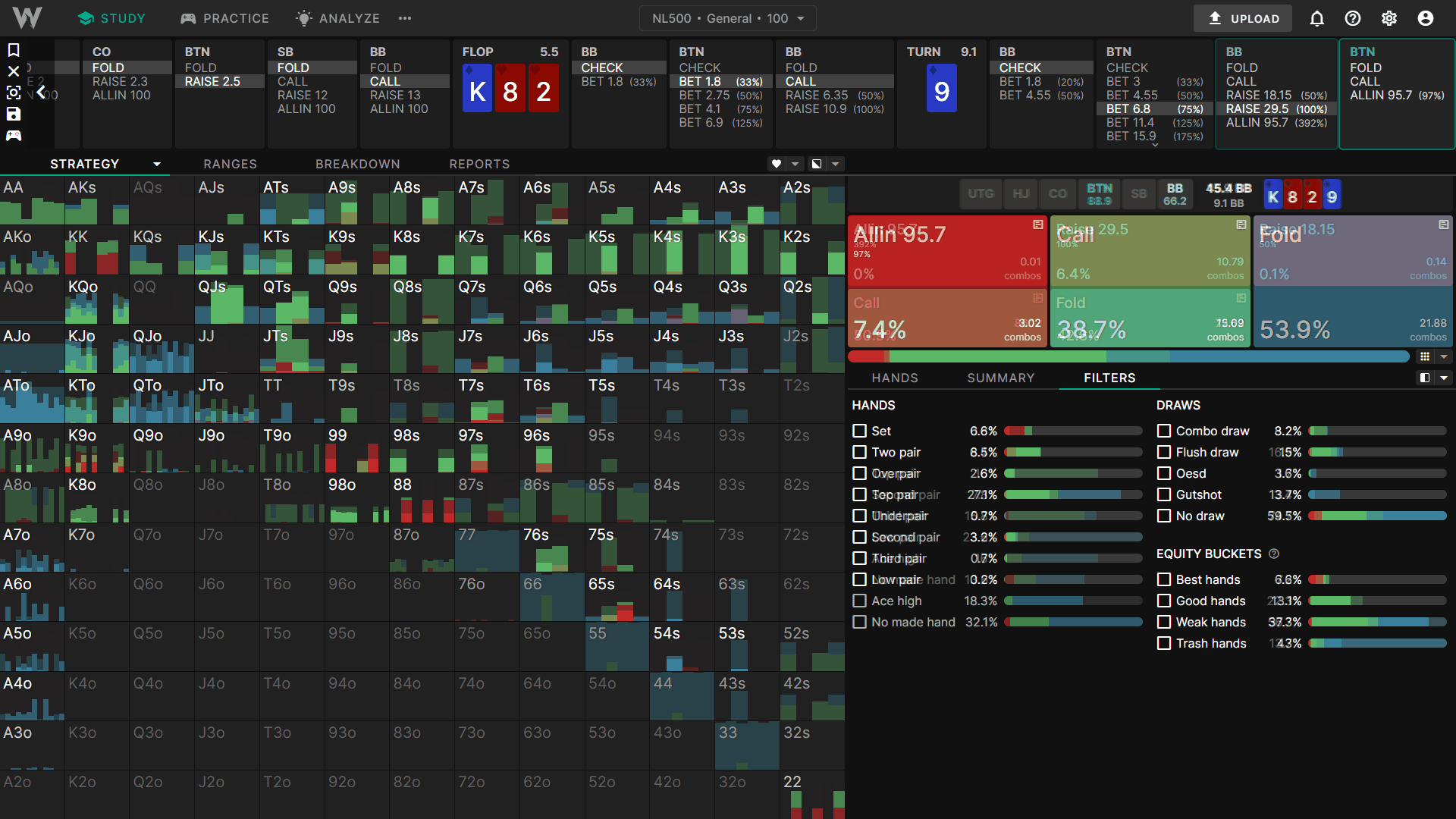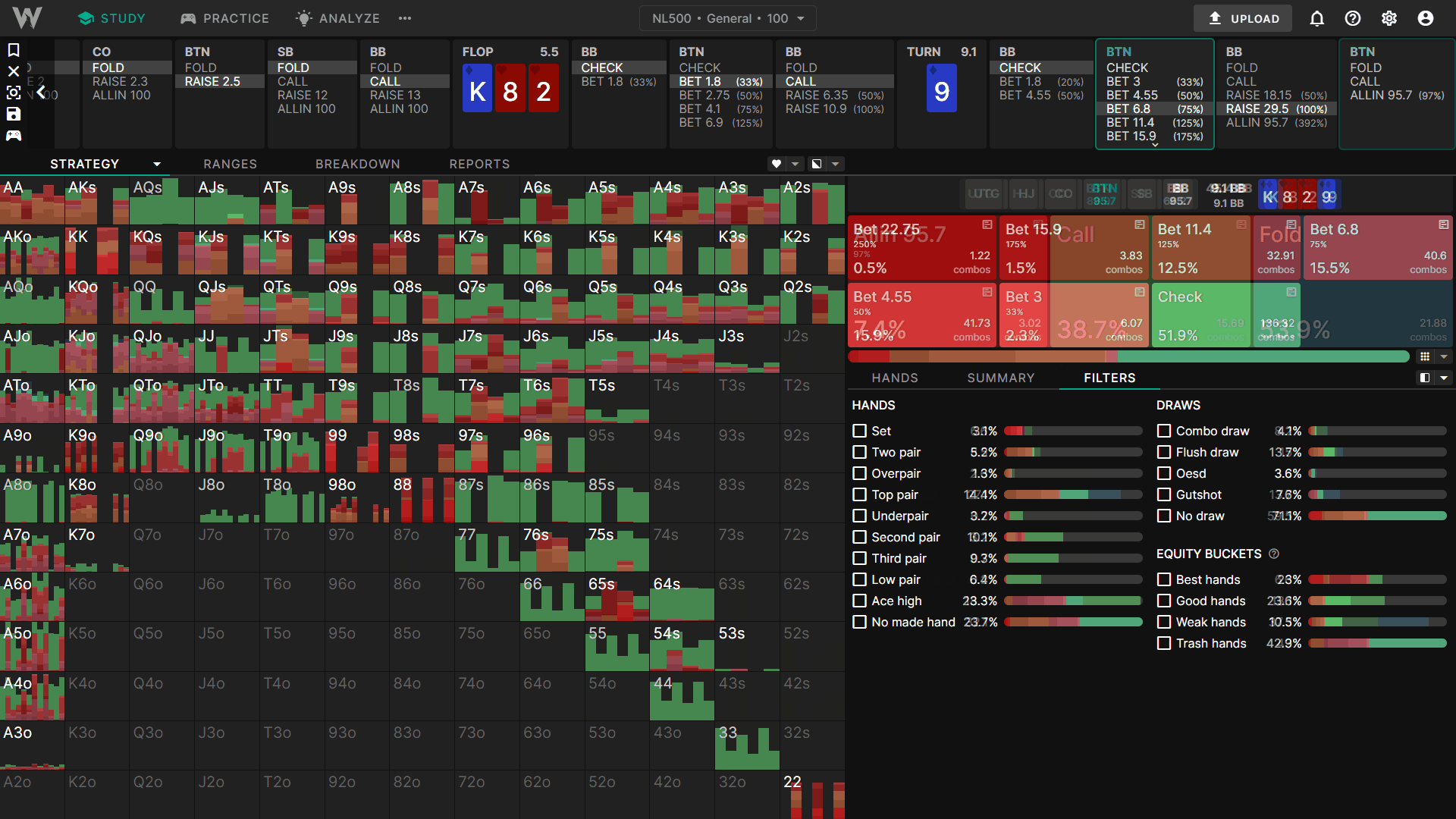
Next we’ll take a look at a turn spot. Here we have BTN vs BB on K♦8♥2♥9♦.

BTN open, BB call
BTN cbet 33% flop, BB call
BB check turn, action on BTN to bet 90% pot or check

In this experiment, we’re going to change the strength of BB’s XR bluffs and observe its effect on our response. We’ll look at three scenarios:

Baseline (GTO)

Here we see the default GTO Wizard strategy on the turn.

Too Polarized (bluffs are too weak)

Now let’s nodelock BB’s check-raise bluffing range. We’ll keep the value range the same (two-pair+ hands), but remove all bluffs/draws and replace it with 43o. 43o has about 5% equity and is as close to a pure bluff as we can get.

As you can see, BTN responds by calling everything. Furthermore, we never need to raise as there’s no incentive to try and fold out 43o. This hand has no equity against our range. Raising only donates to BB’s nutted hands and folds out a complete airball bluff.

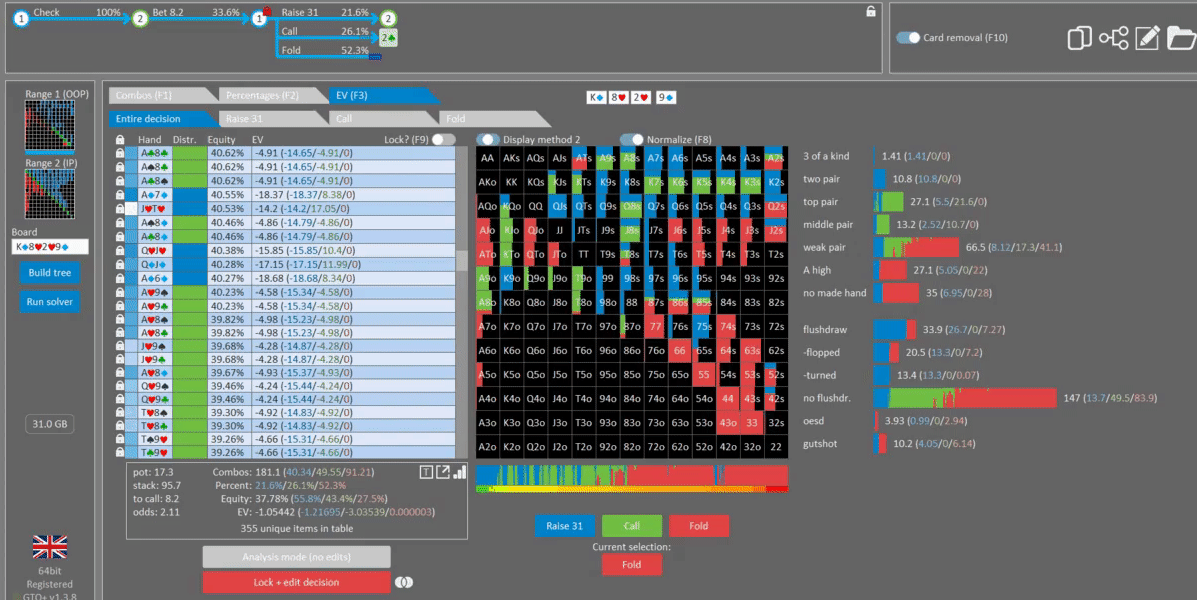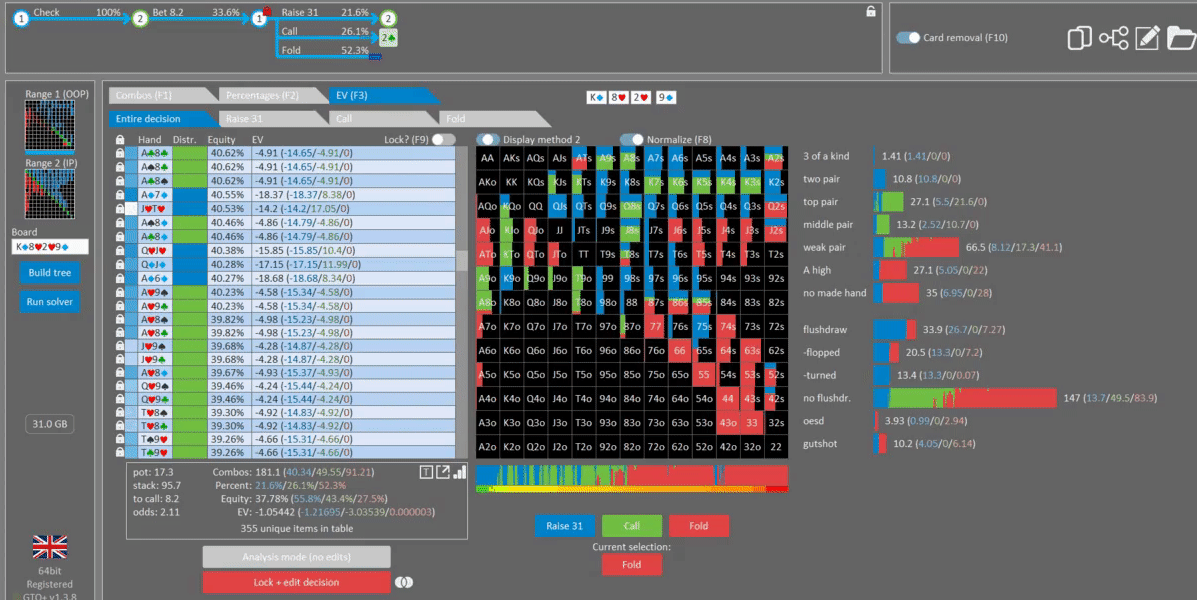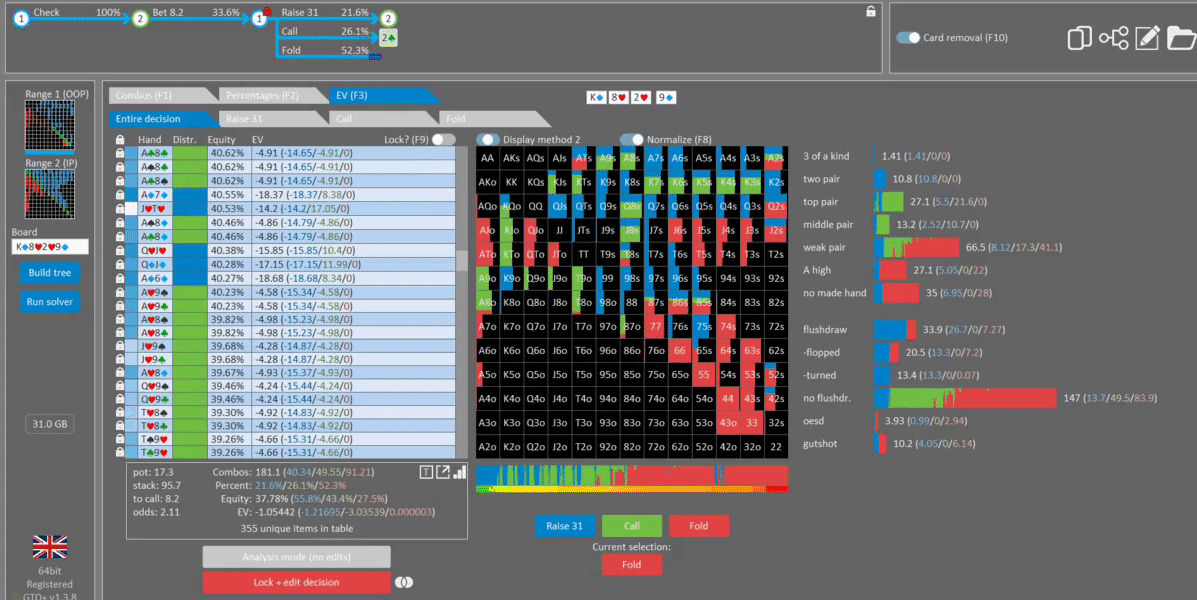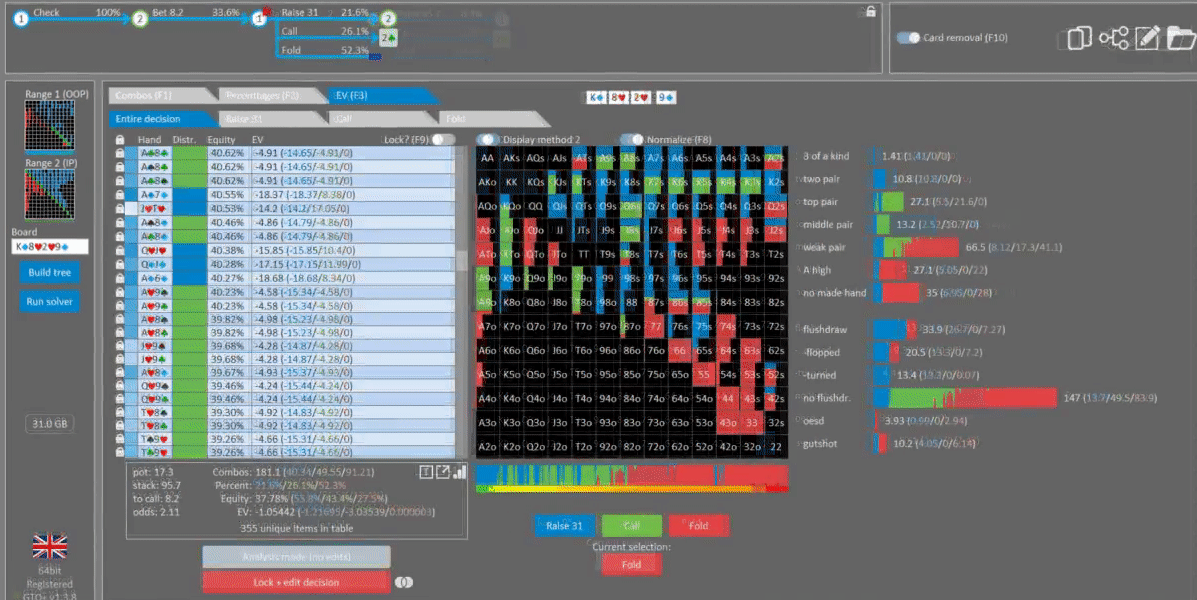
Too draw-heavy (bluffs are too strong)

Next, let’s increase the strength of BBs bluffs. Instead of a GTO range I’ve shifted their bluffs upwards to contain many strong draws which have good equity against the top of our range.

The BTN now responds to this check-raise with a raise/fold strategy, opting never to call. This is because BB’s bluffs are too strong, which decreases the value of calling. Furthermore, we are more incentivized to try and fold out these strong bluffs, which have decent equity against our continuing range.

Results

This experiment shows that the value of a raise is directly tied to the value of fold equity.

If the villain’s bluffs (as defined by hands that fold to a raise) are too weak, the value of fold equity decreases. The optimal response becomes call/fold without raising. The only hands with an incentive to raise are those that can polarize over the villain’s value range, and if you’re calling wide enough, even those value hands prefer to slow play.

Conversely, when their bluffs have too much equity against the top of your range (e.g. raising too many strong draws), the value of fold equity increases drastically. This encourages raise/fold strategies, even if we sometimes jam into a stronger hand.

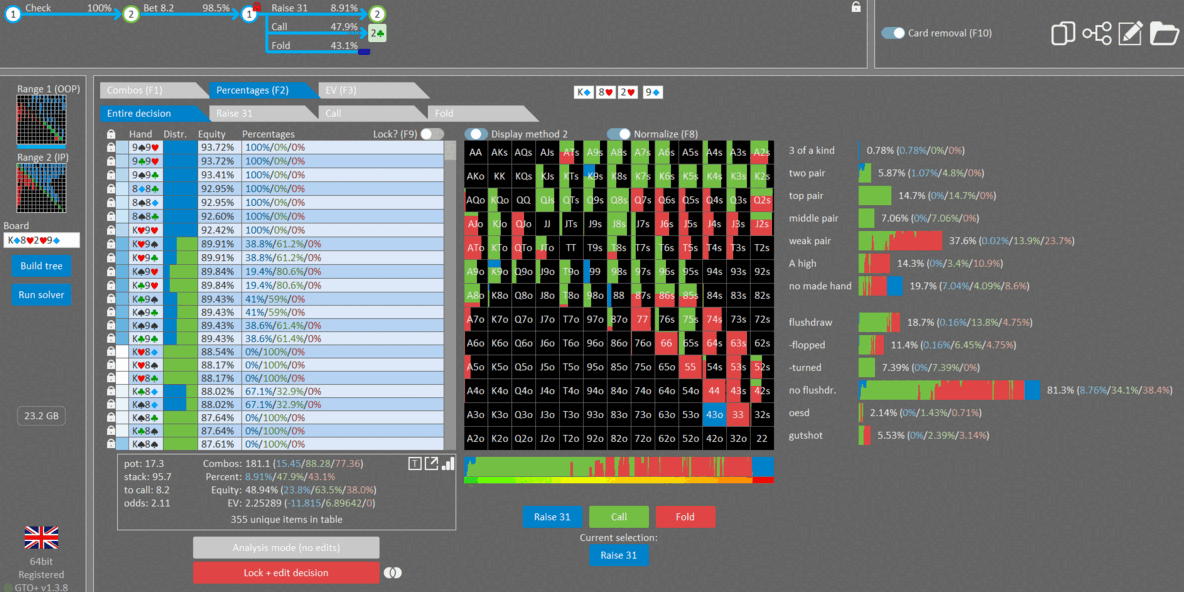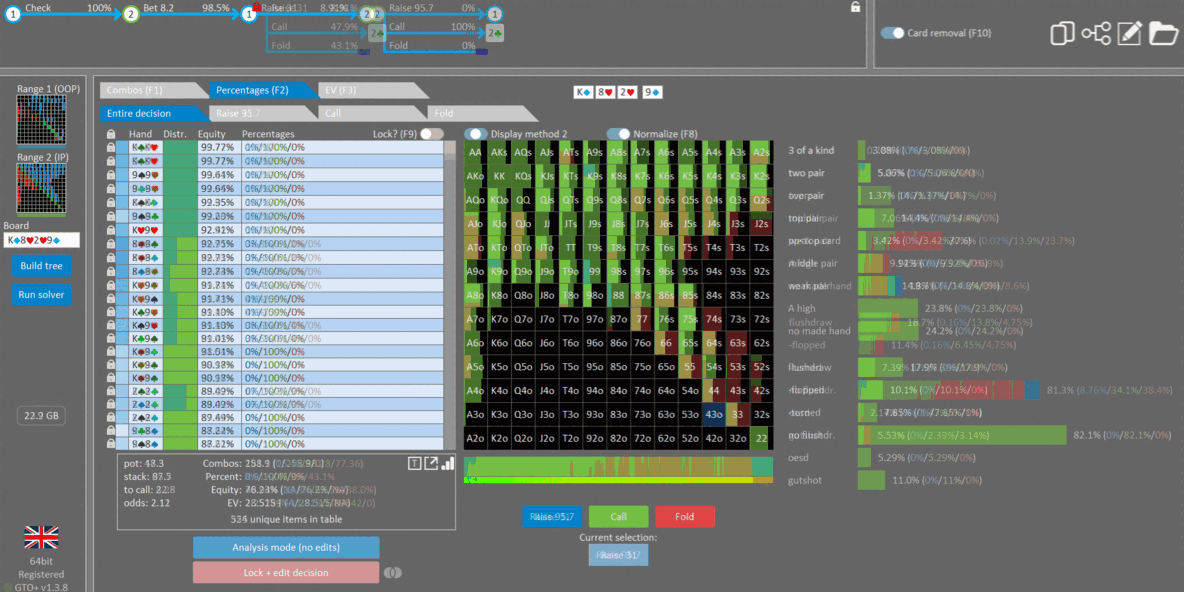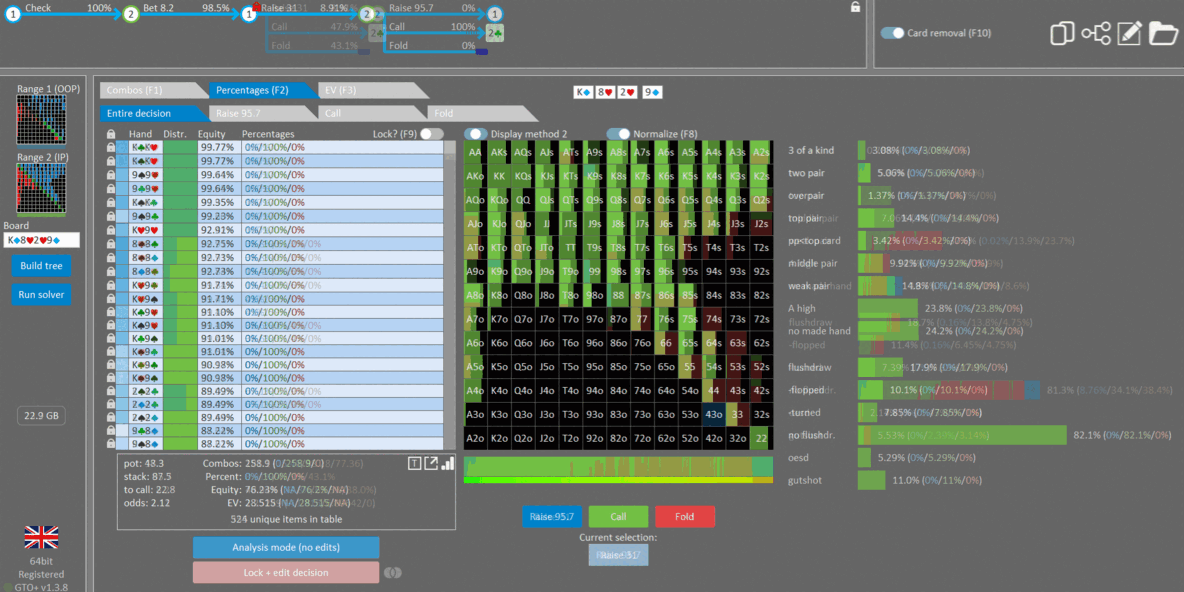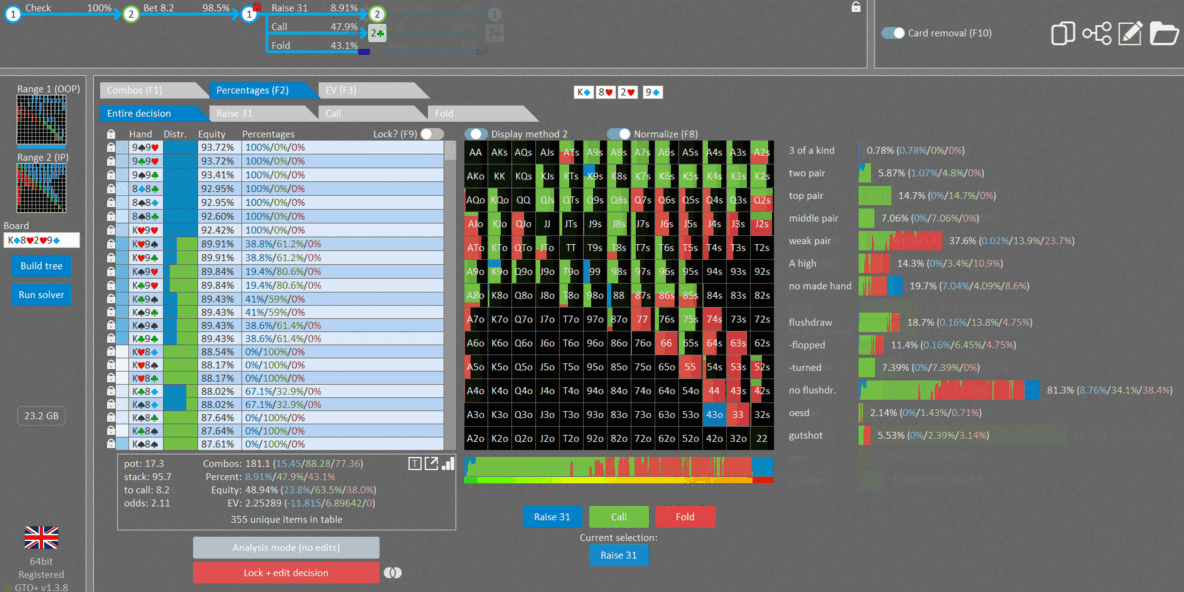
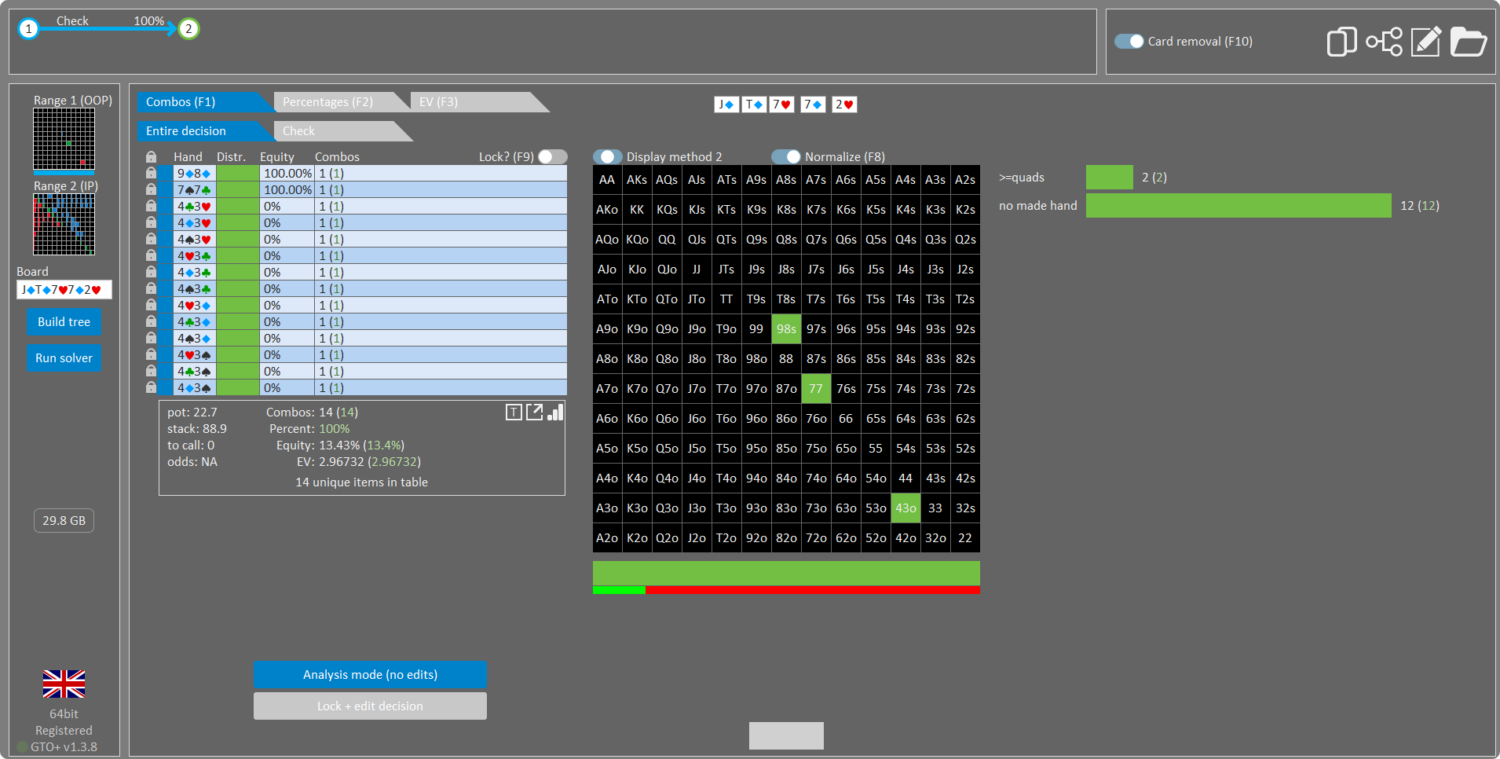
Baseline: Hero’s range (GTO Wizard link):

OOP is nodelocked to check with:

• 1 combo of 77 (nuts)
• 1 combo of 9d8d (nuts)
• 12 combos of 43o (bluffs)

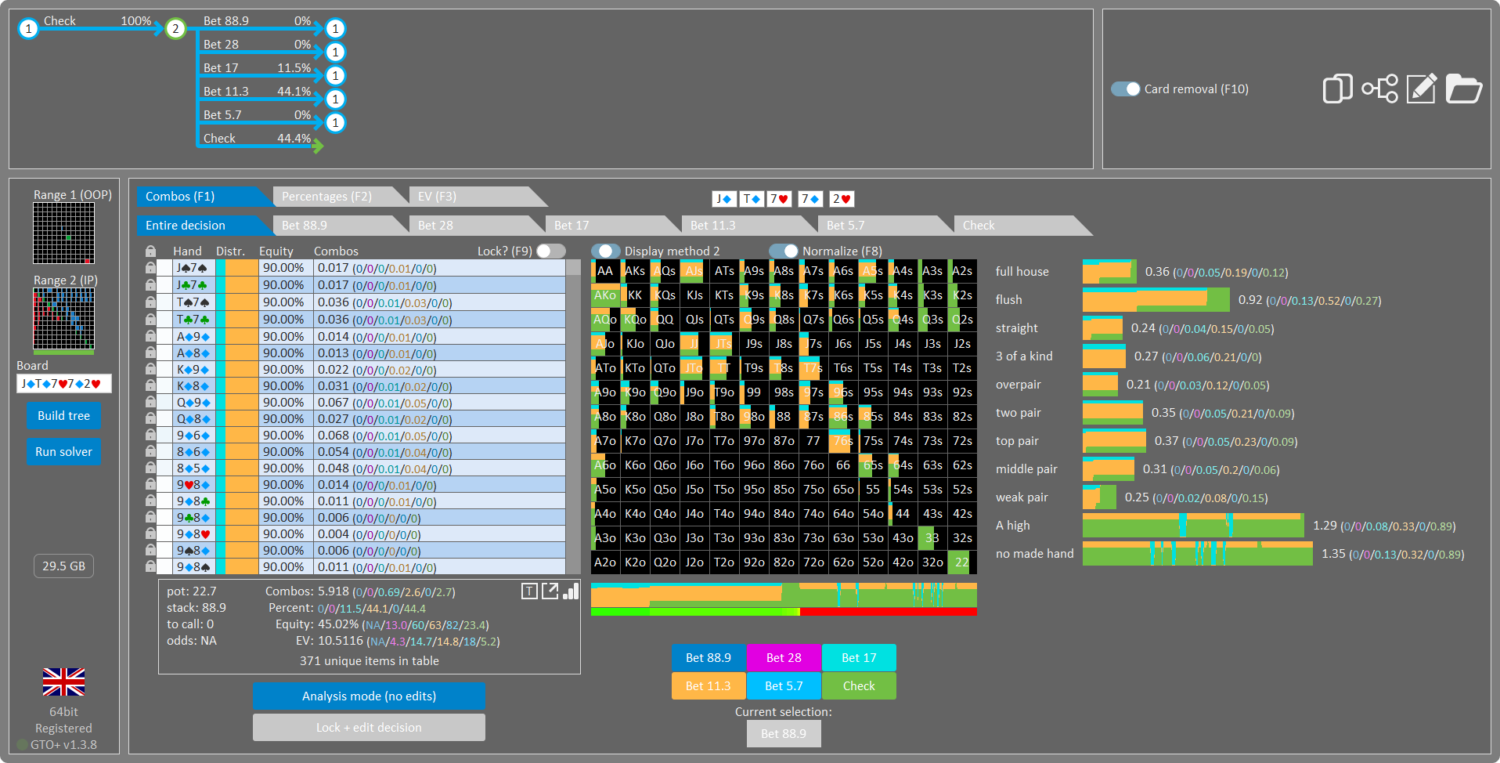
Result: IP rangechecks back, since there’s no value in folding 43o. This makes sense, as 43o has 0% equity against Hero’s range. So betting only folds out worse and gets called by better. This is true for every hand in hero’s range.

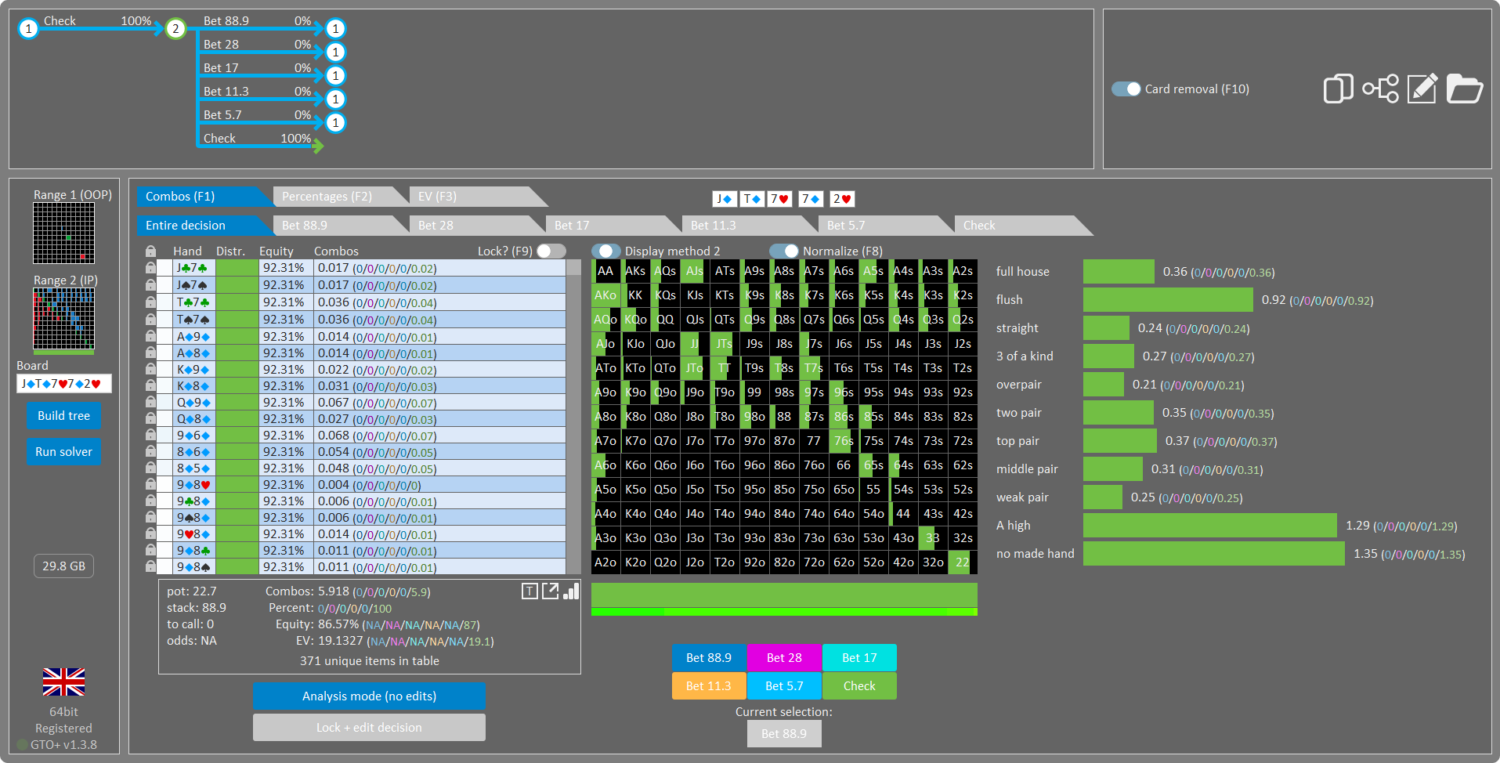
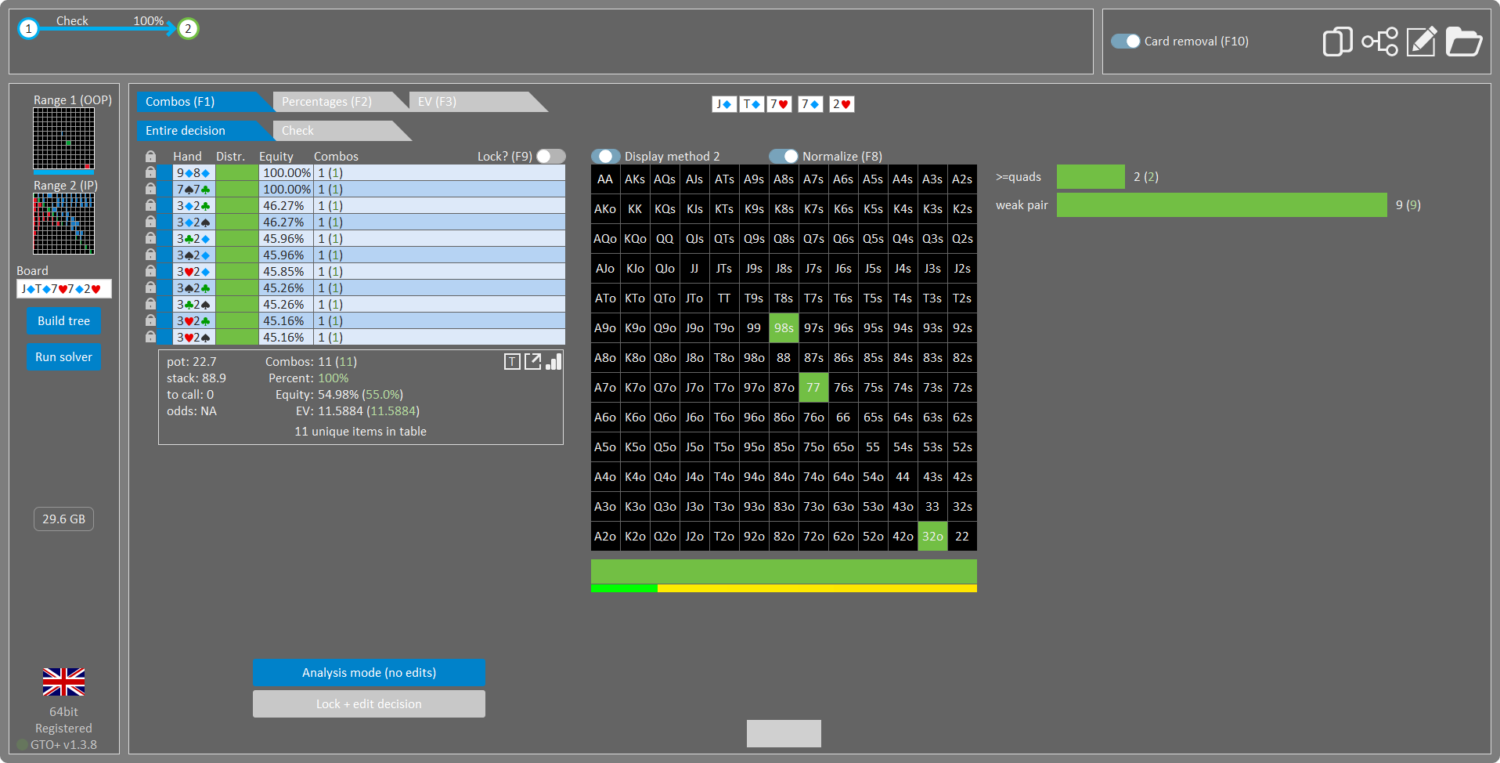
Ok, now let’s change OOP’s 43 to 32, a hand with 45% equity against hero’s range

Result: Hero is betting more than half the time

Conclusion

The value of fold equity is a fundamental incentive to be considered at every decision point. If your opponent folds hands that have no value against your range, then you haven’t actually gained anything relative to checking.

We saw in the flop analysis that fold equity impacts which underpairs prefer to bet.

We saw in the turn experiment that increasing the strength of villain’s bluffs incentivized us to fold/raise rather than call. Decreasing the value of villain’s bluffs incentivized us to fold/call rather than raise.

In the river toy game, we saw that we would never want to bet against a perfectly polarized range. If we increase the equity of the bottom of villain’s range then we are more incentivised to bluff them off that hand.

In summary, you need to consider the value of your opponent’s folding range when deciding to bet.