When ICM Breaks Down

If you have read my previous GTO Wizard articles and my books, you’ll know I am a fan of ICM. I think the Independent Chip Model is something that gets needlessly ignored by a lot of tournament players, which is remarkable since it is likely the most important guiding principle in the biggest money decisions of tournament players – whether that is a tough final table spot or a final table deal, ICM errors heavily influence win rates.
But even though it is highly impactful, ICM is by no means perfect. It has a couple of limitations that you need to be aware of to avoid making a big error. These limitations can be summarized as follows:
- ICM does not take blind levels into account.
- ICM assumes equal skill.
- ICM does not look into the future.
ICM Assumes Equal Skill
We have already discussed this in our article on final table deals. A final table deal is often the place where a player is first introduced to ICM, it is also the place where many players realize perhaps the most fundamental limitation of ICM. A final table deal is a way to reduce variance and the ‘ICM chop’ is currently the best available method we have to assign a real money value to a chip stack.
The problem is that skill or ability is not considered at all! The assumption is that the remaining players are of equal skill and therefore it does not cause changes to the likelihood of finishing at certain places in the tournament.
If a complete amateur makes a final table with the same stack size as Jason Koon, an ICM deal looks like a terrible idea (for the stronger player). An ICM calculation is essentially something that projects finish distributions (solely based on the size of chip stacks) in the tournament and if both Koon and the recreational player had 20bb, an ICM deal would assume they both win the tournament or bust next at the same frequency. This is clearly not the case, Jason Koon is going to win the tournament much more than an amateur.


If a complete amateur makes a final table with the same stack size as Jason Koon, an ICM deal looks like a terrible idea (for the stronger player). An ICM calculation is essentially something that projects finish distributions (solely based on the size of chip stacks) in the tournament and if both Koon and the recreational player had 20bb, an ICM deal would assume they both win the tournament or bust next at the same frequency. This is clearly not the case, Jason Koon is going to win the tournament much more than an amateur.
This is not an issue at a lot of final tables. Edges are small between players these days and final tables tend to be shallow stacked, which leaves less room for skill expression. Most players are happy to give up a small amount of EV for the sake of reducing varianceVariance
Variance measures how far a set of numbers differs from the mean. In poker, variance often refers to how “swingy” a game or strategy is relative to your win rate. Variance can also be defined as the square of standard deviation, usually measured in bb/100., and in the case where one player is clearly superior, they tend to be able to negotiate a better-than-ICM deal.
We have already covered this in the context of final table deals, but what about the strategy itself? ICM calculations were first conceived of as a way to construct final table deals. It was only decades later that it was used to inform strategic decisions! One thing that often gets overlooked during ICM strategy talk is whether very good, or very bad players should follow ICM ranges religiously.
Let’s look at a Toy GameToy Game
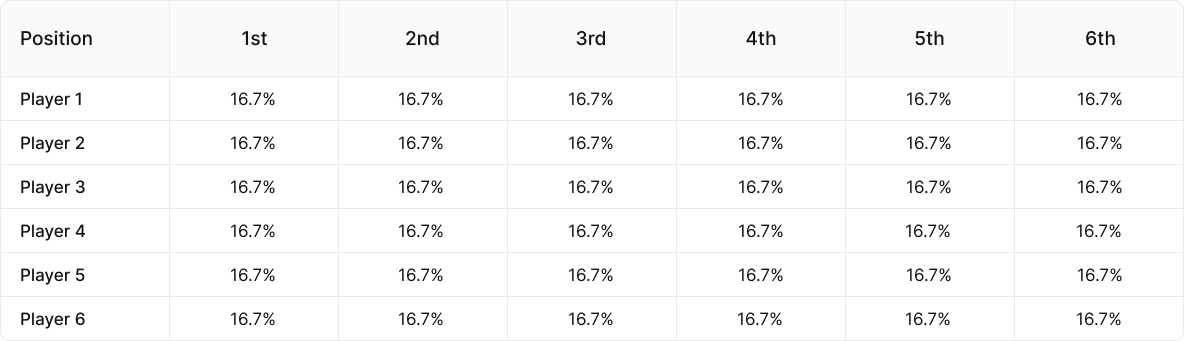
A toy game is a simplified version of poker, that is used to help players understand the underlying principles and strategies of the game. It is often used as a teaching tool to help players learn the rules and mechanics of the game, as well as the concepts of game theory, such as decision-making and probability. example of a $100 6-Max SNG, which pays 60% to the winner and 40% to the runner-up. If you were to do an ICM calculation at the start of the tournament, each player’s stack would be worth $100 (in our rake-free example) and the finish distributions would look like this:
ICM assumes all players are of equal skill, which means that everyone has an identical chance of finishing in every position. Every player would make the money 33.4% of the time.
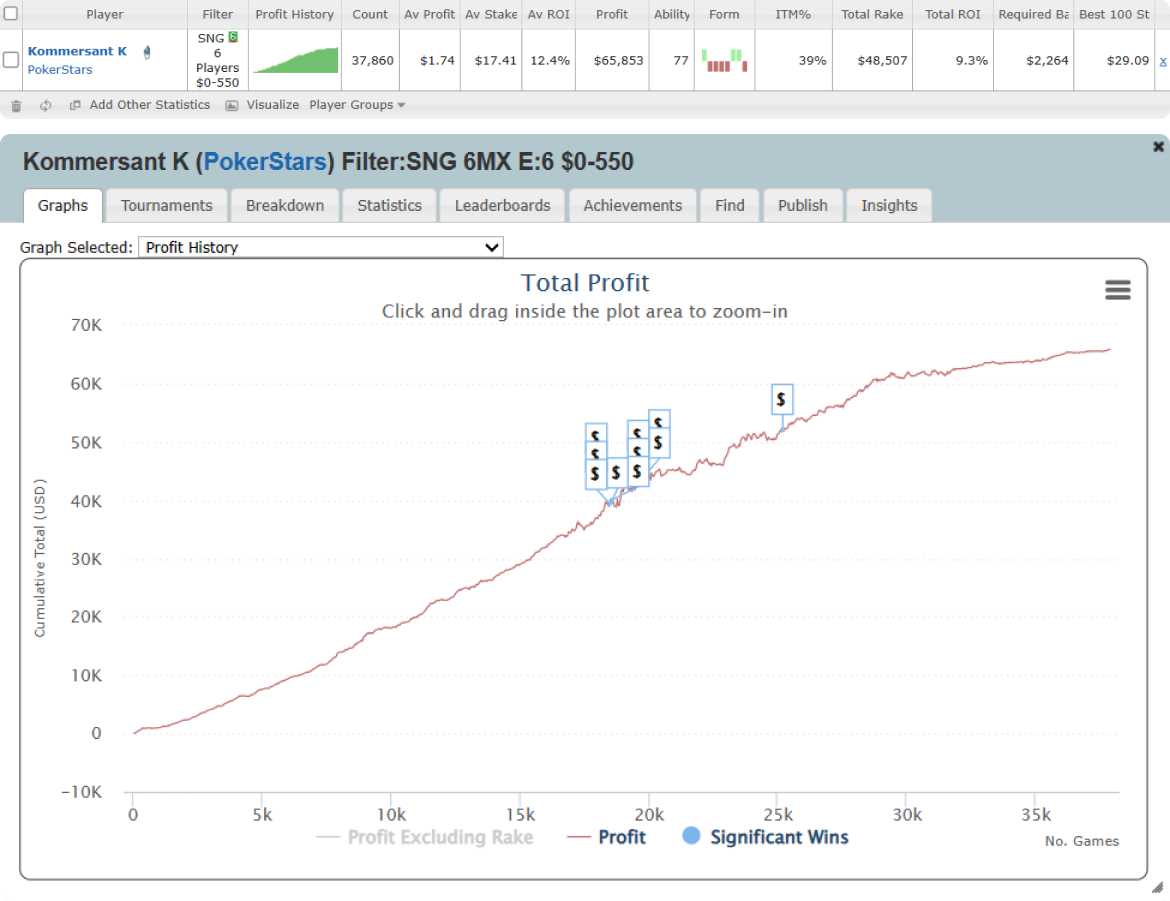
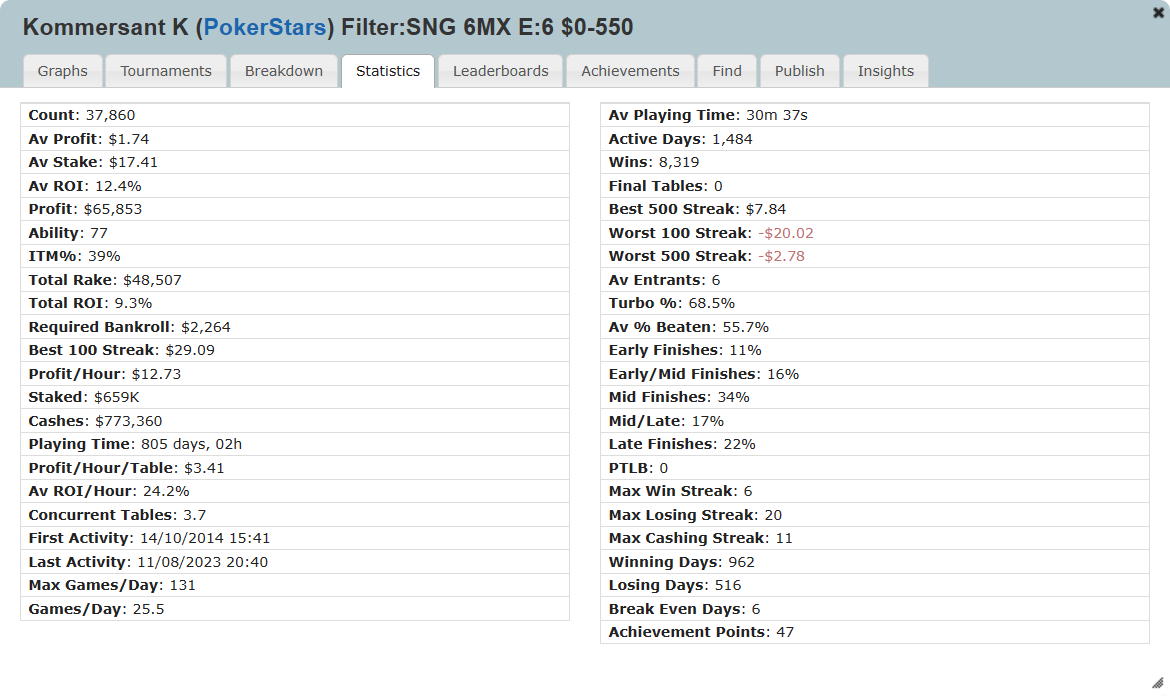
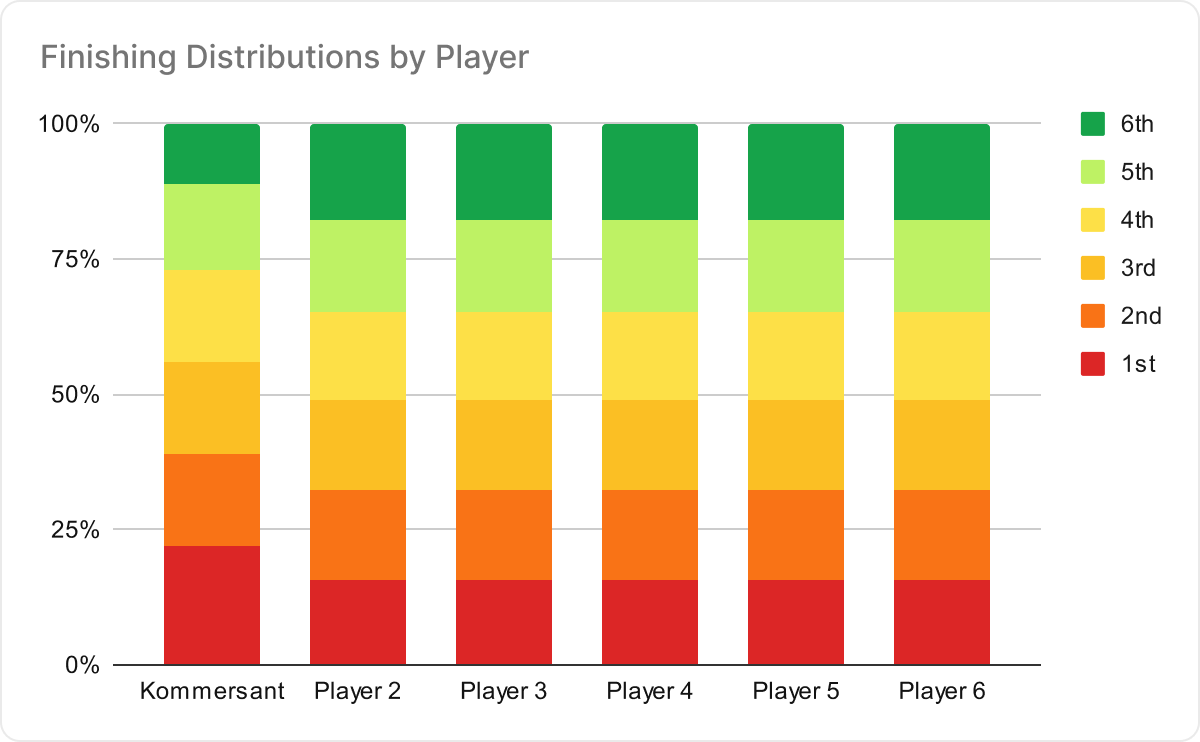
It’s hard to quantify edge against other players, but one thing we can do to get an idea is to look at a large sample from a significantly winning player to see where they are finishing in a tournament compared to the average player. I looked on SharkScope at the Six Max SNG leaderboard and picked one of the big winners at random. This is ‘Kommersant K’ on PokerStars who has played 37,835 6-Max SNGs at the time of writing with an ROIROI
The aggregate money won, divided by tournament entry fees. If you have paid $1000 in entry fees, and won $2000 total, your return on investment is 200%. of 12.4%.
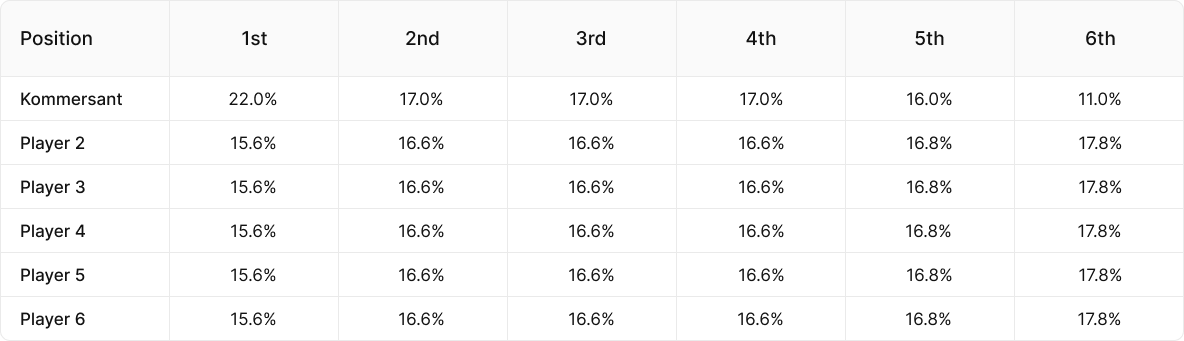
You can almost get a perfect representation of what this player’s finish positions are from his statistics, not quite but close enough:
This player comes 6th 11% of the time, which is much less than the average (which was earlier noted to be 16.7%). They come 5th 16% of the time, which is pretty much average. You can’t see specifically how often they come 3rd or 4th, but combined they finish in the two middle positions 34% of the time, so let’s say they finish 3rd 17% of the time and 4th 17% of the time. They come 2nd 17% of the time, which is a little more than average, but they win 22% of the time which is a big edge.
In total, they finish in the money 39% of the time, compared to 33.4% of the time on average.
Against five other average players, the finish distributions would instead look like this:
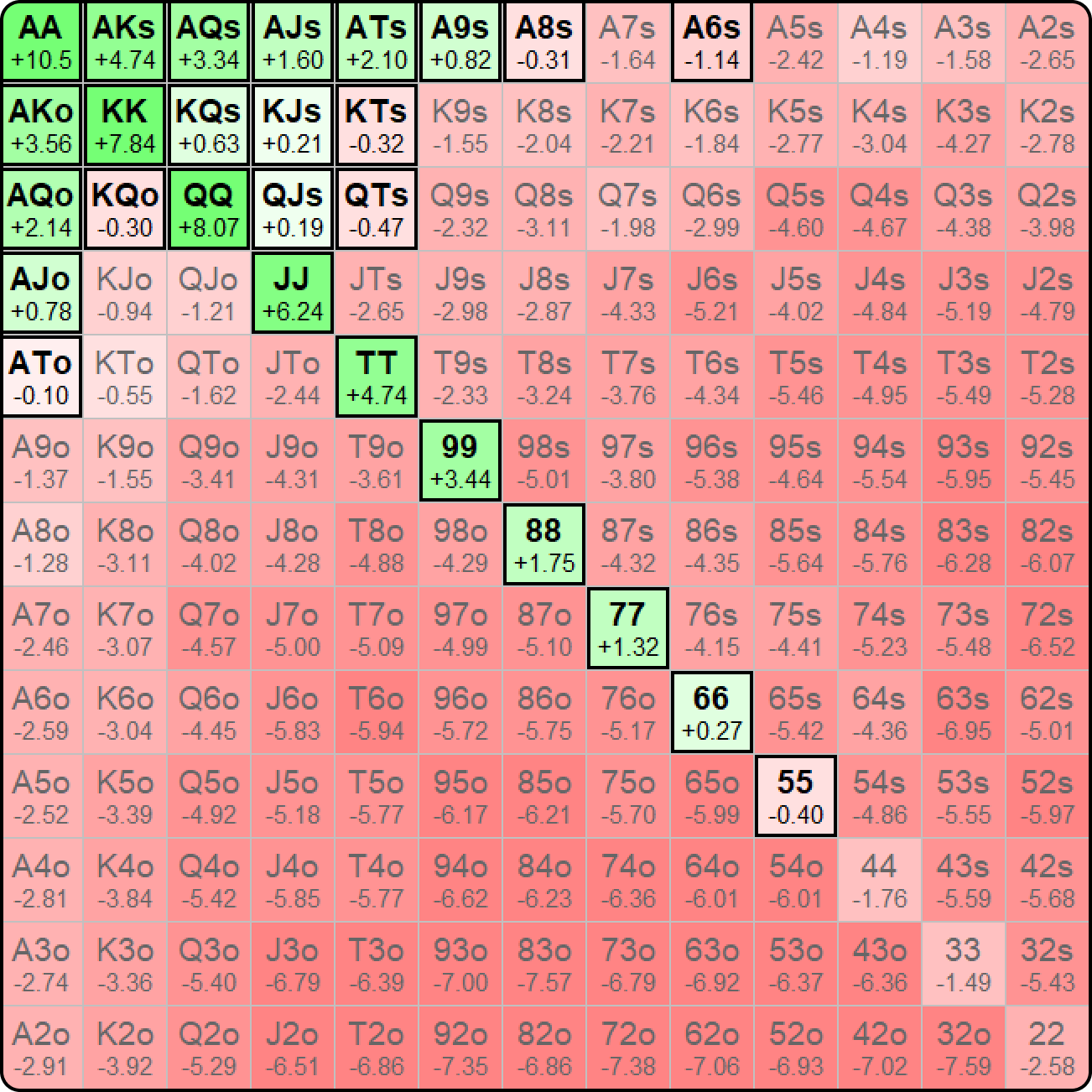
Let’s say we are playing a Hyper-Turbo 6-Max SNG, and on the very first hand the BTN shoves 25bb and it is folds to Kommersant K in the BB. We gave the BTN the option to shove or min-raise, and their shoving range is 44, A5s, AKo, KTs, Q9s+, J9s and T9s. In GTO World, this is what Kommersant K should call with:
There are many snap-calls here, but also many marginal hands that are close to breaking even.
Is it really worth it for a crusher in this tournament to risk their whole stack on such a small edge? We know that, if they folded, they would go on to cash in this tournament 39% of the time. I would argue that this is a good example of when a skillful player should pass up on a small edge that an ICM calculator would say is a call. Calling here feels like an opportunity cost for a crusher in these fields.
Is it really worth it for a crusher in this tournament to risk their whole stack on such a small edge?
Of course, if the other players in this tournament were playing GTO ranges, then Kommersant K would not have the edge he clearly enjoys. Given he is a high-volumeVolume
Volume refers to the amount of hands or tournaments a cash or MTT player plays respectively. player, it is probably likely he is playing something close to GTO, which would mean that part of his success comes from not passing up on small edges like this. I’ve also picked a hyper-turbo spot where nobody should be passing up on any type of edge since skill edge is much lower at shallower stack depths because there’s less room for postflop ‘outplaying’.
The point remains, however, that we know that this player enjoys a skill edge at this table and while calling here with a marginal hand is ICM solver-approved, folding is perhaps the more profitable option. Conversely, a weak player at this table should not be passing up on any small edges.
ICM Does Not Look Into The Future

Because ICM calculations started as a way to settle final table deals, the assumption was naturally that the tournament would end immediately afterwards. This presents a flaw when ICM is used to guide strategic decisions because it doesn’t take into account what happens when the current hand is over and play continues!
This creates a number of problems, the big one being that there is no consideration for the game mechanic of blinds predictably moving around the table. When ICM is used to create an UTG range, it doesn’t consider the fact that UTG is going to post the big blind next hand.
Thankfully some modern poker solvers have factored this in. They have the option to apply Future Game Simulation (FGS) which will reflect in the outputs. This is an enhanced version of an ICM calculation which considers what will happen several hands ahead of the current one.
For example, this is a Holdem Resources Calculator (HRC) range for UTG on the bubble of a 9-person SNG. UTG has 800 chips, everyone else has 1,000 chips, and the blinds are 50/100 with a 25 ante. This is using the traditional Mason-Harville ICM model that assumes the tournament is over after this hand:
What this range does not factor in is the cost of inaction. UTG is the short stack and will have to post 1/8th of their stack the next hand. However, when we use an FGS ICM Model instead, which considers the next three hands too, this is the range:
The range has gone a bit wider to account for the fact that posting the BB is relatively more costly for this player on the next hand.
There is another factor to consider with Future Game Simulation. Not only do we have to take into account the fact that we will post blinds after the current hand, we also have to take into account the fact that blinds can increase after the current hand. The following range is a Future Game Simulation range that also takes into account the fact that the blinds are increasing to 100/200 with a 50 ante the next hand:
Now the range has become significantly wider, to account for the fact that UTG is going to be posting 25% (instead of 12.5%) of their stack the next hand. The cost of inaction has doubled, so UTG takes more risks.
I would go one step further and say that it’s not just that ICM does not look into the future, it doesn’t realize it is in a multi-table tournament. Sometimes the stacks and action happening on another table, even during hand-for-handHand-for-hand
Hand-for-hand is a poker tournament phase when all tables pause and wait for every other table to finish their ongoing hand before starting a new one. This helps organizers track player finishes and stops players from deliberately slowing down to get a better payout. Typically used during or near in-the-money phases of tournaments., have a significant bearing on your decisions. If, for example, there is a micro stack on the adjacent table and/or you have seen an all-in and a call, then that should dramatically put more ICM pressure on your current hand. Some ICM calculators do take the chip distributions on other tables into account, but they cannot account for somebody being all-in on another table mid-hand.
Conclusion
- ICM doesn’t take blinds and blind levels into account and this can be particularly important to understand in very shallow and/or fast structures.
- ICM assumes that all the players are of equal skill. When this is not the case a talented player can make demands in final table deals of the other players. Strategically it means that good players should pass up barely profitable spots and wait for better ones, while weaker players should not pass up on any profitable spots, even the very marginal ones.
- ICM doesn’t look into the future. It doesn’t account for blinds increasing or positions rotating. This is particularly important when the blinds coming back around and/or increasing puts you in a vulnerable position.
- ICM is an incredibly important strategic guide in tournaments and the players who ignore it are burning EV. But ICM is not a perfect model by any means, it has limitations you need to be aware of so you can deviate away from it when the circumstances merit a more comprehensive approach that will force you to think outside of the proverbial ‘ICM-box’.
Author
Barry Carter
Barry Carter has been a poker writer for 16 years. He is the co-author of six poker books, including The Mental Game of Poker, Endgame Poker Strategy: The ICM Book, and GTO Poker Simplified.
Latest article
ICM Does Not Take Blind Levels Into Account
A basic ICM calculation will tell you the value of your stack in terms of money. The variables involved are:
- The payout structure.
- Number of players remaining.
- Number of chips each remaining player has.
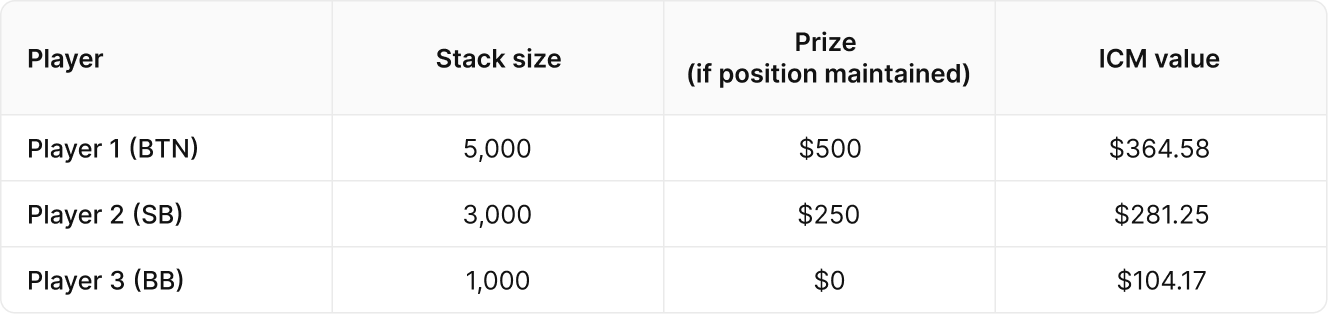
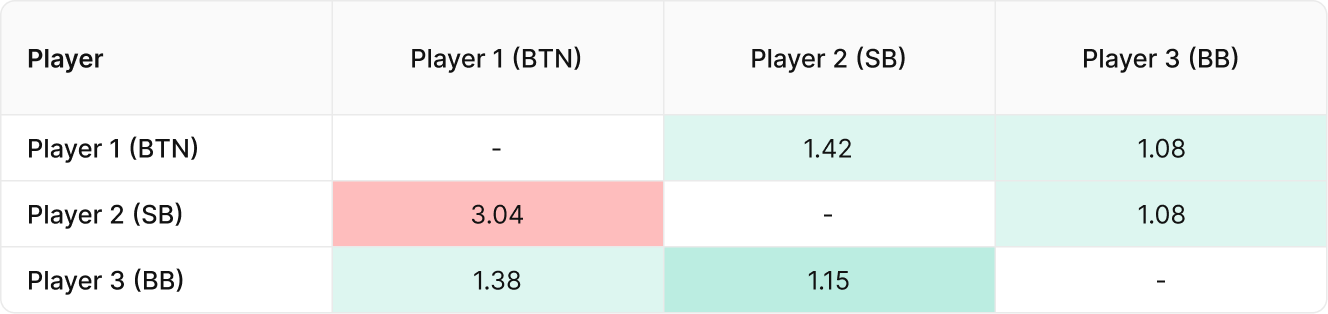
For example, let’s assume we are 3-handed on the bubble of a 6-Max SNG. The situation is listed below for each remaining player with their stack size, (virtual) prize, and ICM value.
ICM is calculated by assessing the chances of every player finishing in every finish position.
The chances of each player winning the whole tournament is their percentage of all the chips in play, but after that, it gets much more complicated.
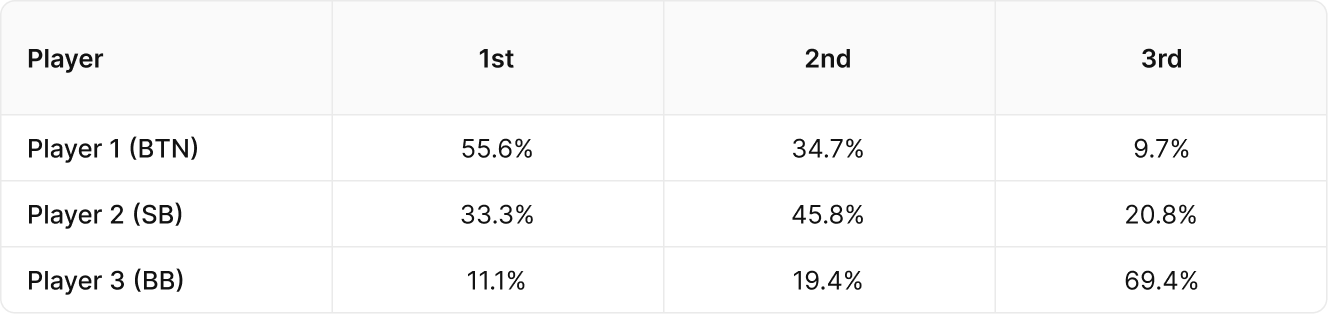
These are the projected chances of finishing in every possible position for our SNG bubble from an ICM calculation:
As you can see, Player 2 has everything to lose here. They are projected to cash almost 80% of the time, and their current ICM value is worth more than 2nd place. It would be a disaster for them to collide with Player 1 on this bubble. These are the Bubble FactorsBubble Factor
Bubble Factor measures how much more losing hurts than winning helps you in MTTs. It’s a measure of survival pressure and a valuable tool for understanding ICM spots. It’s defined as the ratio between how much tournament equity ($EV) you’d lose getting stacked, divided by how much $EV you’d gain stacking some player in the tournament.
BF = | $EV Loss / $EV Gain | when stacks are fully invested. Each player pair has a unique bubble factor.
In a chip EV scenario, the BF is 1 because losses are equal to wins. In an ICM scenario, losses hurt more than wins, so the BF is greater than 1. In a bounty format, BF can drop below 1 due to the potential reward of winning bounties., which reflect this:
If you have read our article on Bubble Factor you would know that Player 2 would need 75% equity to break even against Player 1, assuming Player 1 shoved. What we haven’t discussed yet is the blind level. What if the blind level was 3,000/6,000 with a 6,000 Button Ante? That would essentially force all three players all-in.
In this example, in order for Player 1 to finish last, Player 3 needs the best hand, Player 2 needs the second best hand, then in the following hand Player 1 would need to lose again to bust out. Given all three players are essentially playing blind with random cards, the odds of first hand occurring as stated earlier is 16.67% and the odds of Player 1 having the worst hand of the three players in the following hand is 33.33%. 16.67% multiplied by 33.33% is 5.56%, which is the actual percentage chance that Player 1 comes last.
An ICM calculation will show you that Player 1 has a 9.7% chance of bubbling this SNG, but in this example, the actual odds are only 5.56%! The chip leader has a far greater chance of not bubbling (and winning) this tournament than ICM would suggest! This may sound like an extreme example, but it is not completely unrealistic. Hyper-Turbo formats can replicate scenarios not unlike this and I once played a freeroll where this stack dynamic was almost in play at the final table. There are also SNG formats where the players are forced all in when a time limit is reached, which replicate this scenario precisely.
The broader takeaway is that when stacks get shallow enough, there is an inflection point where an ICM calculation becomes less reliable, and the big stacks are at an even bigger advantage.