The Absurd Game Theory of Chopped Boards

A “chopped board” in poker is one where the community cards make up the best 5-card hand for the majority of hands in both players’ ranges. This is often called “playing the board”. Chopped boards lead to fascinating, often counterintuitive strategies. In this article, we’ll dive into the absurd mathematics of chopped boards.
Before we get started, watch this video by Qing Yang to learn more about the theory of “Playing the board”.
Case 1) Everything Chops
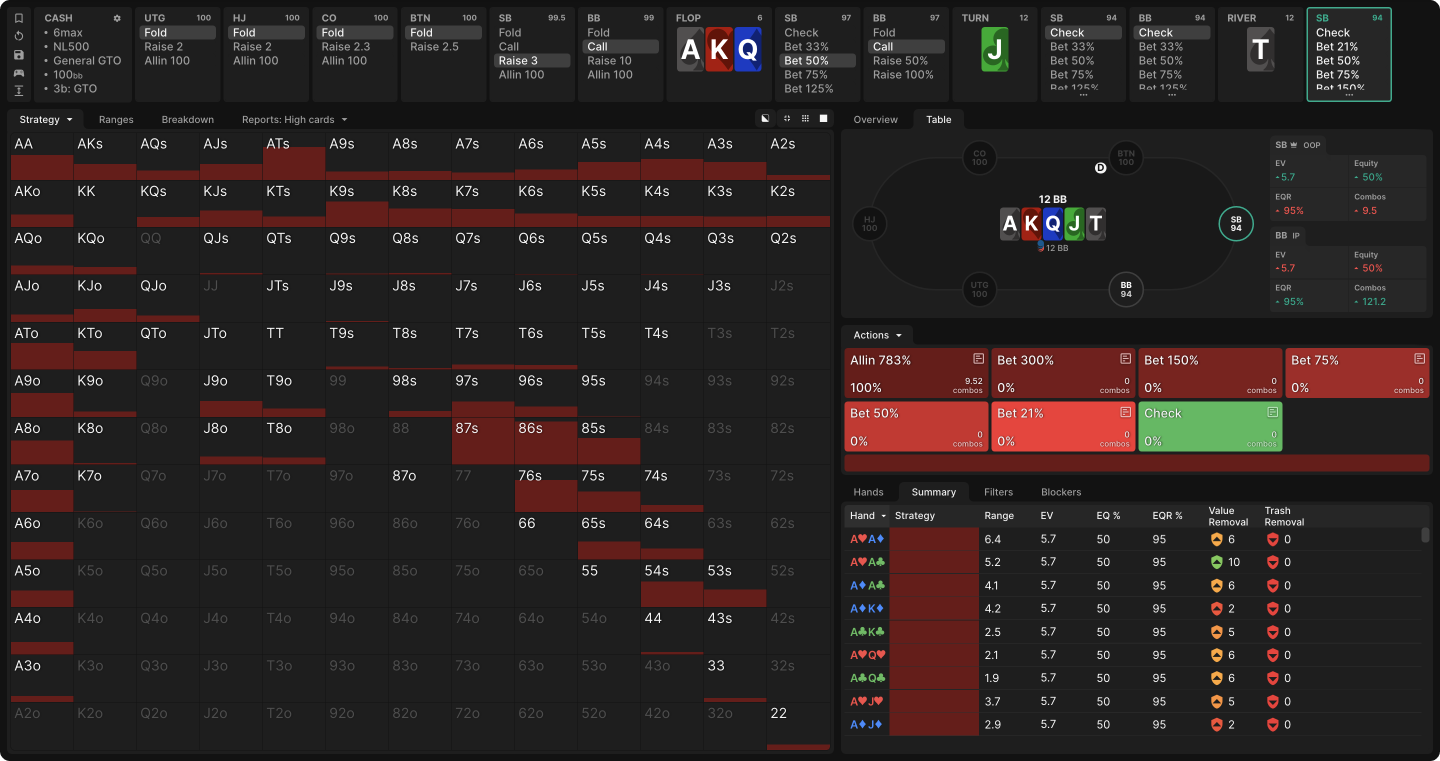
The most obvious example of chopped boards is something like AKQJT rainbow, or AAAAK. The strongest hand either player can make is already on the board. So any strategy that doesn’t involve folding should be good. However, what happens if this is a cash game and rake is involved?
What is SB’s best strategy if this was a NL50 cash game? What is their best strategy if this was a NL500 cash game?
- NL50 Rake Structure: 5% rake, 4bb cap
- NL500 Rake Structure: 5% rake, 0.6bb cap
In the NL50 example, any bet we make will be called, causing both players to pay more rake. Therefore, the best strategy is to check-range and try to showdown without donating more money to the house.
However, in the NL500 example, we’ve already reached the rake cap (0.6bb cap / 5% = 12bb maximum raked pot). Therefore, we don’t pay any additional penalty if we bet. Furthermore, betting allows BB to make a mistake (folding), so betting weakly dominates checking. For this reason, the SB shoves their entire range!
The Prisoner’s Dilemma
Okay, but what happens if we pay a lot more rake or if the bet is much larger? Is it possible to leverage the rake against your opponent to force them to fold? Surprisingly, the answer is yes!
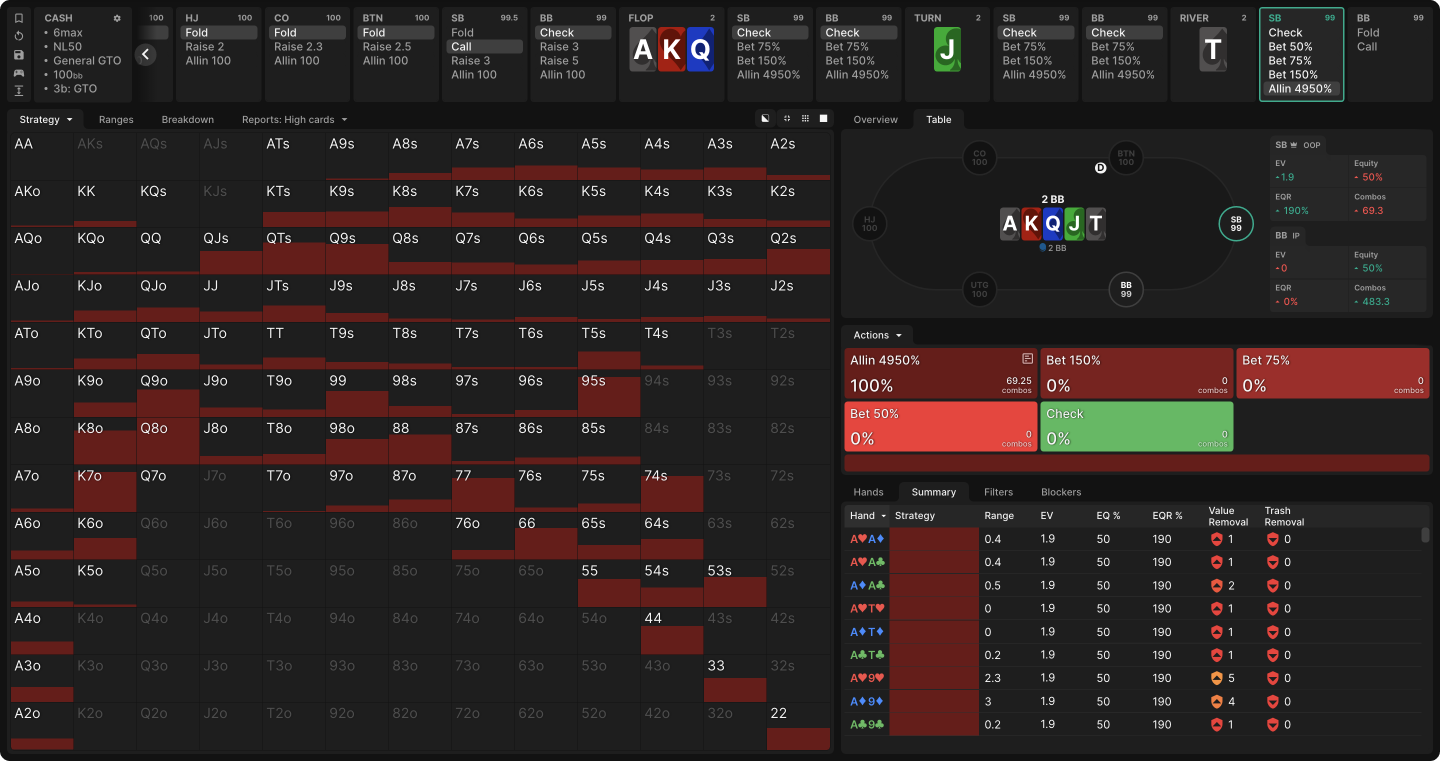
Daily Dose #305 explores a peculiar variation of this toy game. What if the NL50 scenario above was a limped pot that checked to the river? The optimal strategy, surprisingly, is to shove 99bb into a pot of 2bb, a 4950% pot-sized shove.
This shove forces BB to fold everything. If BB calls, they win half the pot (1bb), but they pay 2bb in rake. Therefore the highest EV decision is to forfeit the pot!
The first player to shove should win the pot. Hilariously, BB’s best strategy in a real game would be to shove out-of-turn order before SB has a chance to act! But let’s assume you’re playing online and can’t do that.
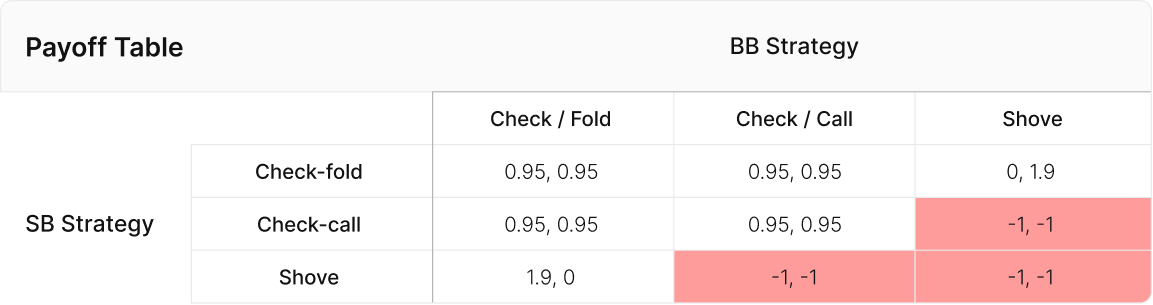
Is folding the best strategy facing this shove? The BB can “spite call”, forcing both players to pay 2bb in rake. This is where the prisoner’s dilemma comes in. Is it correct for BB to spite-call sometimes in order to deter SB from bullying them?
The following payoff table shows the expected value for all strategy pairs. Note that any strategy which involves both players getting stacks in results in a negative payoff due to rake. Ideally, both players check down the pot. However, one can try to force the other to fold to gain an advantage. This is the definition of a prisoner’s dilemma, except in this scenario, the IP player knows the opposing player’s move.
In 1981 Robert Axelrod hosted a tournament to find the best strategy in a game of Repeated Prisoner’s Dilemma. As it turns out, a simple strategy called “Tit For Tat” was the strongest. This strategy would start by cooperating, then retaliate if the opponent betrayed them. It was quick to retaliate, but also quick to forgive. However, this strategy is designed for the repeated game. In poker, this chopped spot occurs so rarely that the short human memory overshadows the point of “Spite Calling” or setting up retaliatory threats.
Case 2) Only some hands chop
Case 2 is the far more interesting version of this game. In this scenario, some hands chop, but others beat those chops. For example, an AKQJT board where flushes are possible.
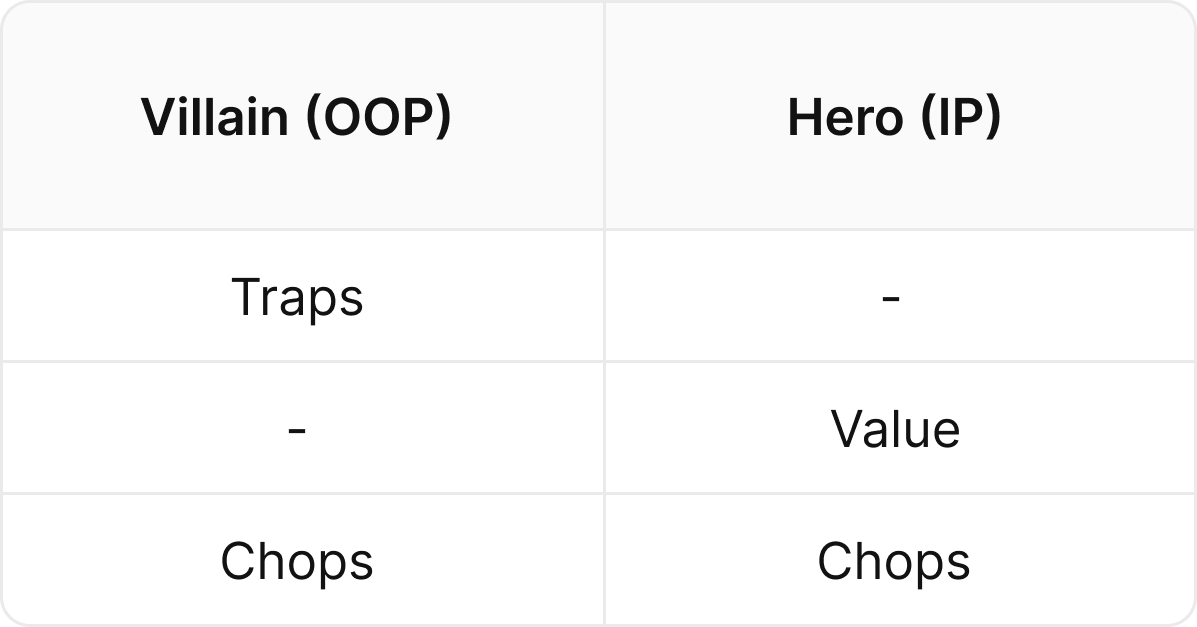
Let’s start with a simple toy game. There are three hand classes: Traps, Value Hands, and Chops. Villain’s checks a range of chops, and a few nutted traps. Hero has value hands that also beat chops, but lose to traps.
Traps > Value > Chops
In the original version of this toy game, hero needs to find the optimal bet size in order to extract maximum value from bluff-catchers, without donating too much to villain’s traps. However in this game, there are no bluffs or bluff-catchers. All chops split the pot with each other. This dynamic changes everything.
Bluffing Frequency
In a “typical” polarized vs. bluff-catcher toy game, the amount of bluffs you need to remain balanced is determined by the pot odds laid. If you over-bluff, then villain can gain EV by always calling you, whereas under-bluffing can be exploited by them folding all their bluff-catchers.
Goal – Make villain’s chops indifferent between calling and folding.
On a chopped board, your goal is the same, to make them indifferent between calling and folding. However, the reward of calling is much smaller in this case. When they call correctly, they only win half the pot (compared to the entire pot plus your bet in a typical bluff-catching scenario). This means the reward for calling is fixed, but the risk of calling still scales with the size of the bet.
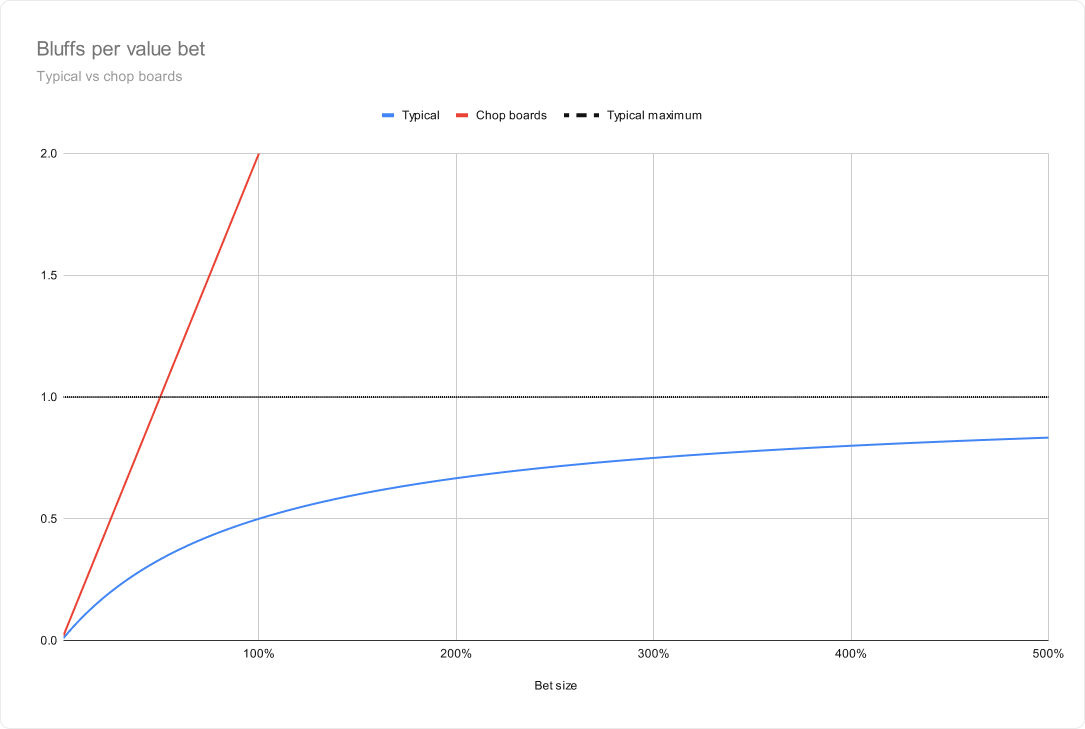
Note that the bluffing frequency skyrockets compared to traditional polarized spots. In a traditional polarized scenario, your bluffs per value bet are equal to the alpha equation, s / (s+1), where ‘s’ is the bet/pot.On a chopped board, your bluffs per value bet equals 2s, twice the size of the bet. The main takeaway here is that you should be bluffing far more often on chopped boards with value compared to polarized spots.
Calling Frequency
How often should villain call the bet? This is a surprisingly complicated question. Well, we know that if we bet too big then villain will fold everything but their traps. But smaller sizes are harder to calculate. To solve this, we first need to ask what equations like MDF and Alpha are trying to calculate. The defending player’s goal is to make our chops indifferent between bluffing and checking behind.
Goal – Make Hero’s chops indifferent between bluffing and checking.
To do this, we set the expected value of each action equal to each other, then solve for the calling frequency.
EV (Check Chop) = EV (Bluff Chop)
The following explains how to derive defending frequencies on chopped boards:
The EV of checking behind with a chop is a function of how many traps villain has.
EV (Check Chop) = (1 – traps%) * pot / 2
The EV of bluffing a Chop is more complicated. The expected value is a function of how much equity we have when called and how often villain folds, both of which are dependent on our bet size.
Let’s start by writing the formula with words.
EV (Bluff Chop) = (Fold% × pot) + Call% {(How often we get called by chop × 0.5 pot) – (How often we get called by trap × bet size)}
Defining variables:
- Call% = c
- Fold% = 1 – c
- Traps% in villain’s range = t
- Bet / Pot = s
- Traps% in calling range = t/c
- Non-traps% in calling range = 1-t/c
Plug in variables and reduce:
EV (Bluff Chop) = (1 – c) + c ( (1 – t/c) / 2 – st/c)
Set EV (Check Chop) equal to EV (Bluff Chop) and solve for c:
(1-t)/2 = 1-c + c((1-t/c)/2 – st/c)
c = 1 – 2st
Villain will never fold a trap no matter how large we bet, so the actual MDF formula becomes:
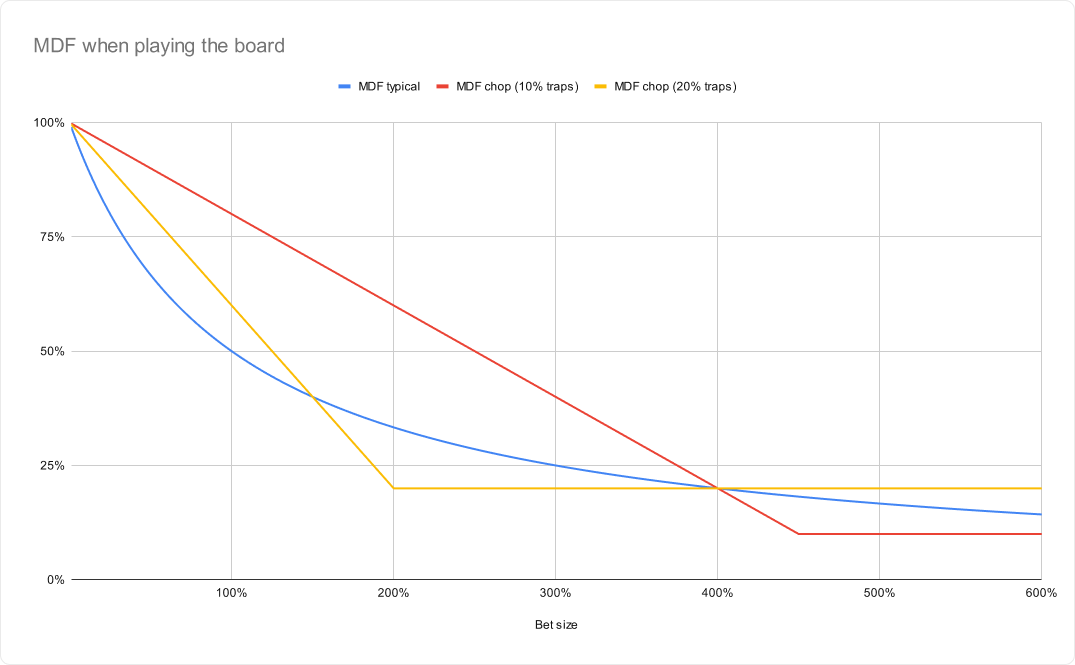
Call% = Max (t, 1 – 2st)
Unlike the curved MDF line we see in a “typical” polarized vs bluff-catcher toy game, on chopped boards, MDF is a linear line that slopes downwards relative to the number of traps in range. If you bet large enough, they don’t need to defend anything but traps, causing their defense frequency to flatten out and remain constant.
EV Curves by Bet Size
These expected value graphs show hero’s total expected value, as a percentage of the pot, according to their bet size. For simplicity, we’re assuming villain can only call or fold. In a typical polarized vs. bluff-catcher toy game, the highest EV bet size is a function of how many traps villain has. We’ve covered this in the How to solve toy games article.
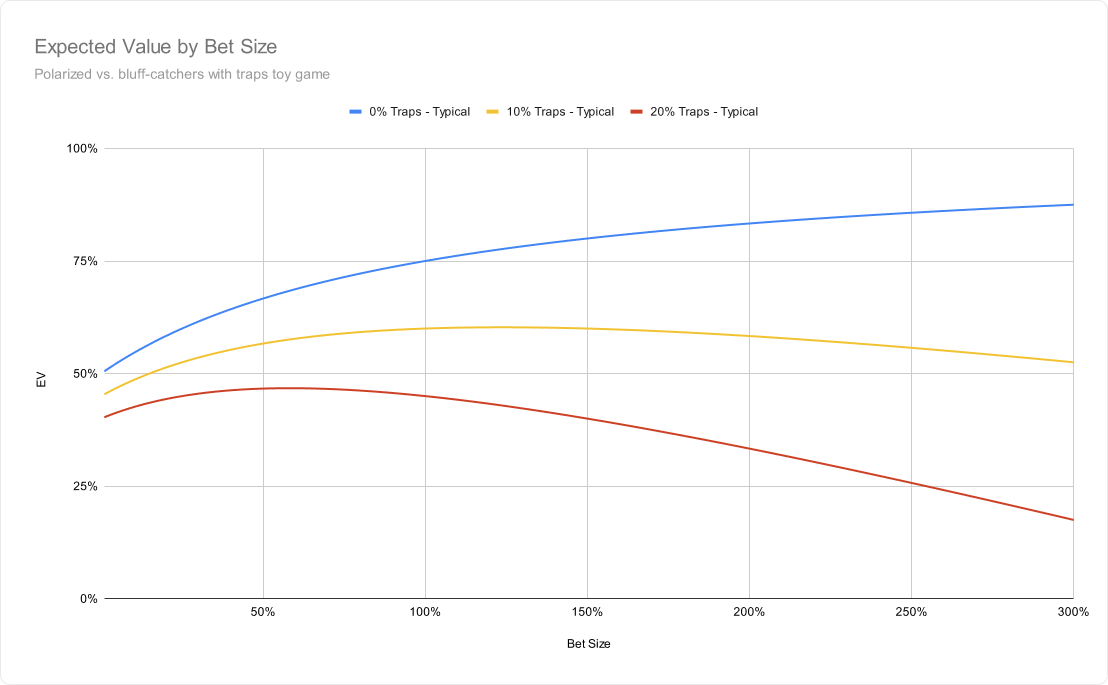
In a scenario with no traps, hero’s optimal river strategy is to shove (or bet geometrically on earlier streets, in order to shove on the river). If villain has traps, hero should bet smaller in order to avoid making the defending range too strong. The following charts assume hero starts with 50% value hands and 50% bluffs (then bluffs or gives up optimally depending on sizing).
In our chopped toy game scenario, things change. The expected value of betting hits an “inflection point” where hero runs out of bluffs. From that point on, betting larger only serves to decrease the EV of your value bets.
Hero should have X% bluffs for every value bet, where X is equal to twice the size of the bet. For example, when putting in a 150% pot-sized bets, hero should bluff 3 chops for every 1 value bet, in order to make villain indifferent to calling their “chop-catchers.
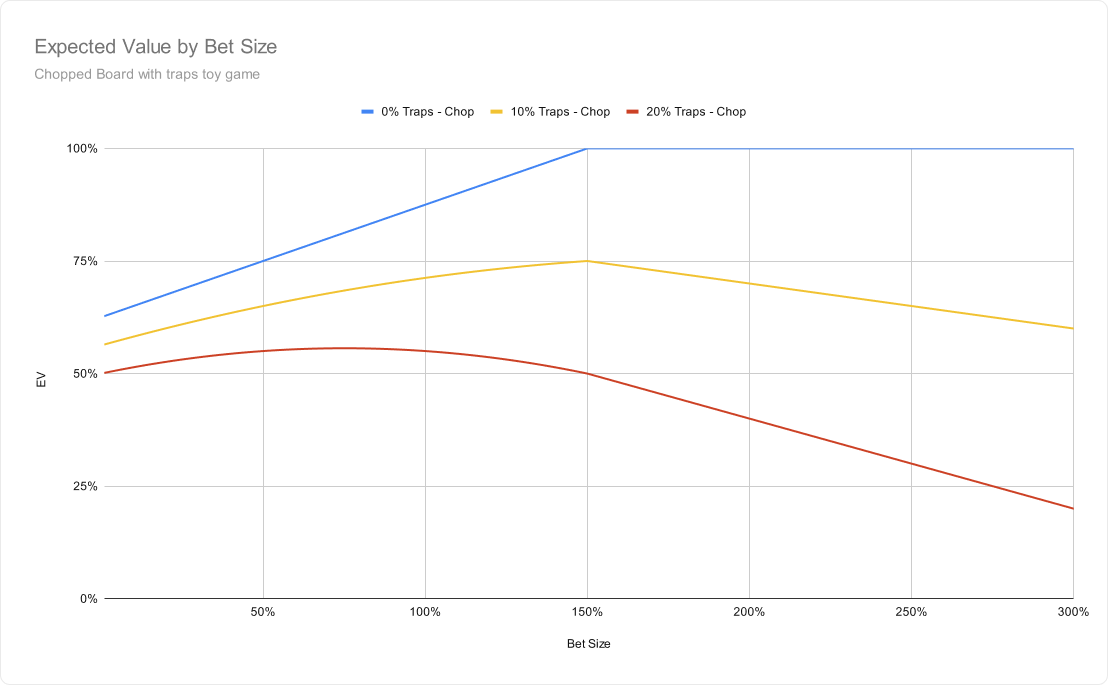
The following graph shows hero’s EV by bet size. Here we assume hero starts with 25% value hands, and 75% chops. At s = 150% we run out of bluffs, so that sets the theoretical maximum bet size. However, if villain has at least half as many traps as we have value bets, then the optimal bet size can become smaller, as is shown by the red line below where the villain has 20% traps in range.
Conclusion
The toy game above is relatively simple. The player with traps is pacified, and none of the hands block each other. In a real game there are far more variables involved. Players can raise and re-raise. Sometimes the only nutted hands you could have would block your opponent from having those hands.
However, we can still learn several key takeaways from this chopped board toy game:
- Bluff more often on boards where a large portion of your range chops.
- You will often run out of bluffs and should therefore range-bet these boards.
- Typically that means you should also call wider on these boards.
- How wide you should defend overall is a function of how many traps you have.
- Pay attention to the rake structure. If you can’t make them fold, then it may not be worth unnecessarily increasing the pot and paying more rake.
Author
Tombos21
Tom is a long time poker theory enthusiast, GTO Wizard coach and YouTuber, and author of the Daily Dose of GTO.