The Limitations of Nash Equilibrium in ICM Spots
In the complex world of poker tournaments, the Independent Chip Model (ICM) plays a pivotal role in decision-making. However, when diving deeper into game theory and ICM, players may come across counterintuitive results that challenge conventional understanding. This article aims to explore the limitations of Nash Equilibrium (GTO) in ICM spots.
In this article, we will demonstrate:
- How different Nash Equilibria have different EVs
- Why minimum EV is no longer guaranteed
- How a GTO strategy can lose EV against mistakes
- Why adding actions can decrease EVs
Nash Equilibrium in Non-Zero-Sum Games
In a two-player zero-sum game, the sum of the payoffs for all players is zero for any combination of strategies. This means that one player’s gain is exactly balanced by the other player’s loss. If you play GTO (also known as a Nash Equilibrium strategy) in a zero-sum game, you get some valuable guarantees:
✅ Minimum EV Guarantee: By playing GTO, you are guaranteed to achieve at least a certain amount of expected value (EV).
✅ Your opponent’s mistakes can only benefit you.
✅ Adding actions (such as extra bet sizes) to your strategy can only benefit you.
✅ Your opponent cannot push you into a worse Nash Equilibrium.
These features are well-known and are what attract most people to GTO in the first place. However, these guarantees only apply to heads-up (HU) zero-sum games!
Tournament poker appears to be zero-sum. After all, the total sum of prizes and chips doesn’t change. However, when chips move between two players, it’s not only their $EV that’s affected. The tournament equity of every single player in the field changes.
In tournaments, the sum of payoffs between two players in a pot is no longer zero.
Some of their $EV can get leaked to the rest of the field.
If the sum of payoffs (between the two active players) is not zero, things break!
🟥 Minimum EV Guarantee: By playing GTO, you are guaranteed to achieve at least a certain amount of expected value (EV).
🟥 Your opponent’s mistakes can only benefit you.
🟥 Adding actions (such as extra bet sizes) to your strategy can only benefit you.
🟥 Your opponent cannot push you into a worse Nash Equilibrium.
To be clear, Nash Equilibrium still works and is well-defined in non-zero-sum games. Your opponents cannot gain EV against a GTO strategy. But the aforementioned guarantees no longer hold.
EV Leakage
When you win a pot in a tournament, even though you gain the chips, the overall distribution of tournament equityTournament Equity
Tournament Equity is your expected share of the remaining prize pool, as predicted by the Independent Chip Model. changes for the entire field. If you knock a player out, everyone moves up in rank, and each remaining player expects to win a larger proportion of the remaining prizes. Some of the value you capture “leaks” to the other players in the field. By “value,” we mean the monetary value of your stack as predicted by the ICM model, also known as tournament equity, which we will abbreviate as $EV.
This can go both ways, however. $EV can be gained from or lost to the rest of the field. When you even out the stacks, such that both players are closer to the average stack, this tends to leach $EV from the rest of the field.
Example One: Satellite Bubble
The simplest example is the bubble of a satellite tournament where three players remain and only two are paid:
- Satellite: Top 2 places win
- 3 players remain
- Symmetrical 10bb stacks
- No ante
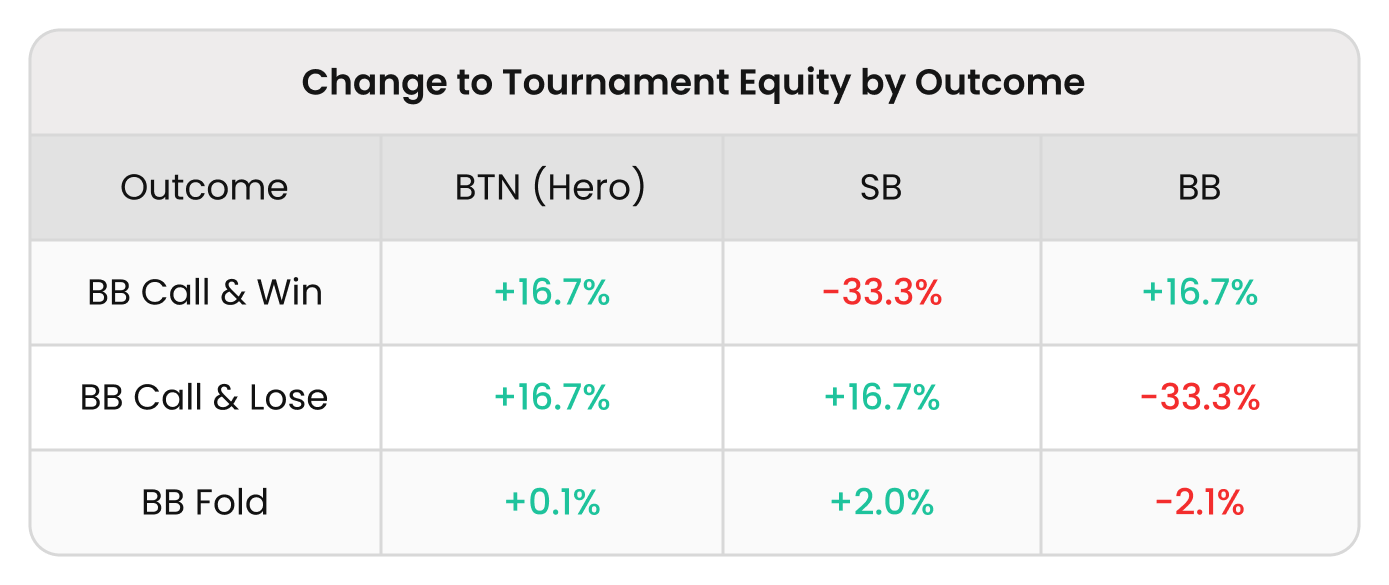
You fold on the Button (BTN), the Small Blind (SB) shoves 10bb, and the Big Blind (BB) is left to act. Note that regardless of the outcome, you gain $EV. If one of them stacks the other, you win a ticket. Even if the BB folds, your tournament equity increases from 33.33% to 33.46%. SB and BB are “leaking” $EV to you. In tournaments, your $EV can change despite your stack staying the same!
This is the clearest concept of $EV leakage. In tournaments, the monetary value of your stack ($EV) can change despite your stack staying the same in terms of chips.
Example Two: 200 Entries Bubble Spot
Next, let’s examine a 200-player classic bubble spot:
- $200 buy-in; $40,000 in prizes remaining
- 40bb symmetrical stacks
- 30 places paid; 33 players remaining
- Standard GTO Wizard prize structure
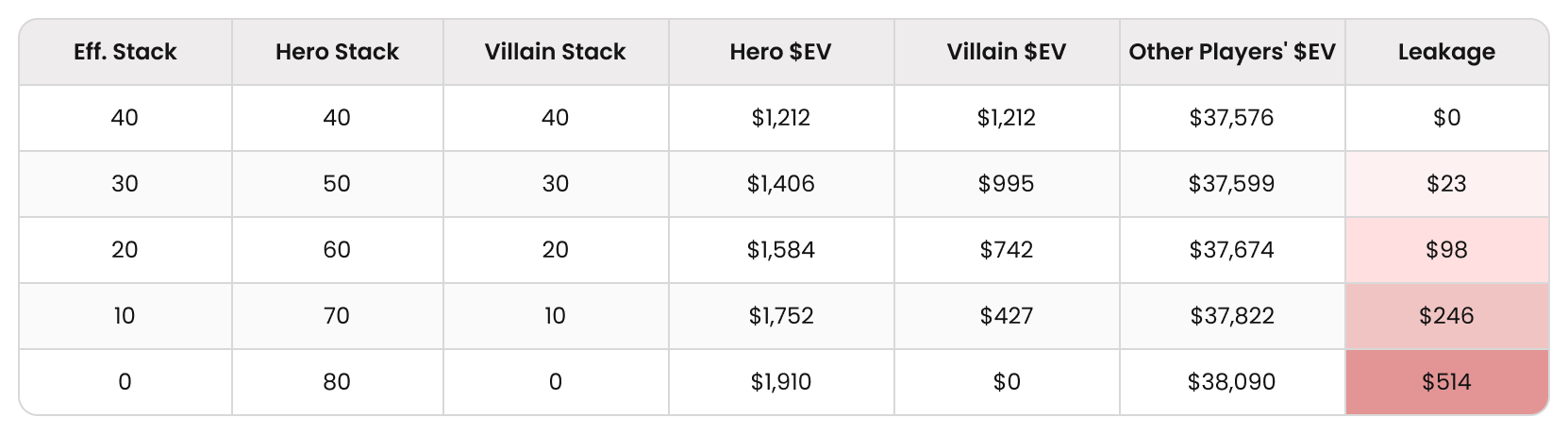
When two players clash, they leak $EV to the rest of the field. The more chips you win from your opponent, the more $EV you leak! In this spot, since stacks are symmetrical, everyone starts with 1/33 tournament equity ($EV) = $1212.12.
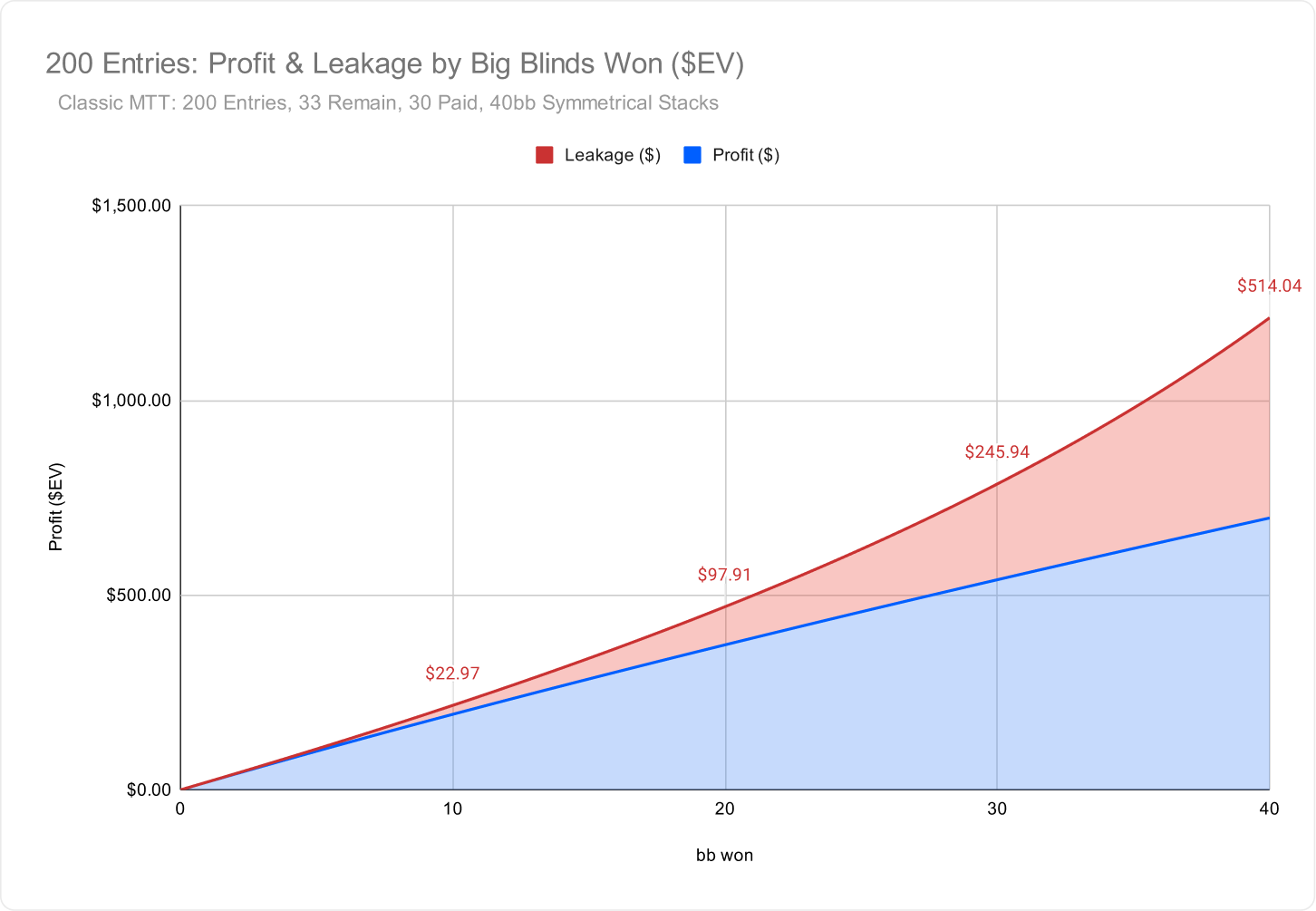
As you take chips off of your opponent, the value of your stack increases, but so does the value of everyone else’s stack. If you knock someone out, doubling up, they will lose $1212, and you will gain $698 in tournament equity. The remaining $514 is distributed to the rest of the field who are now closer to the money.
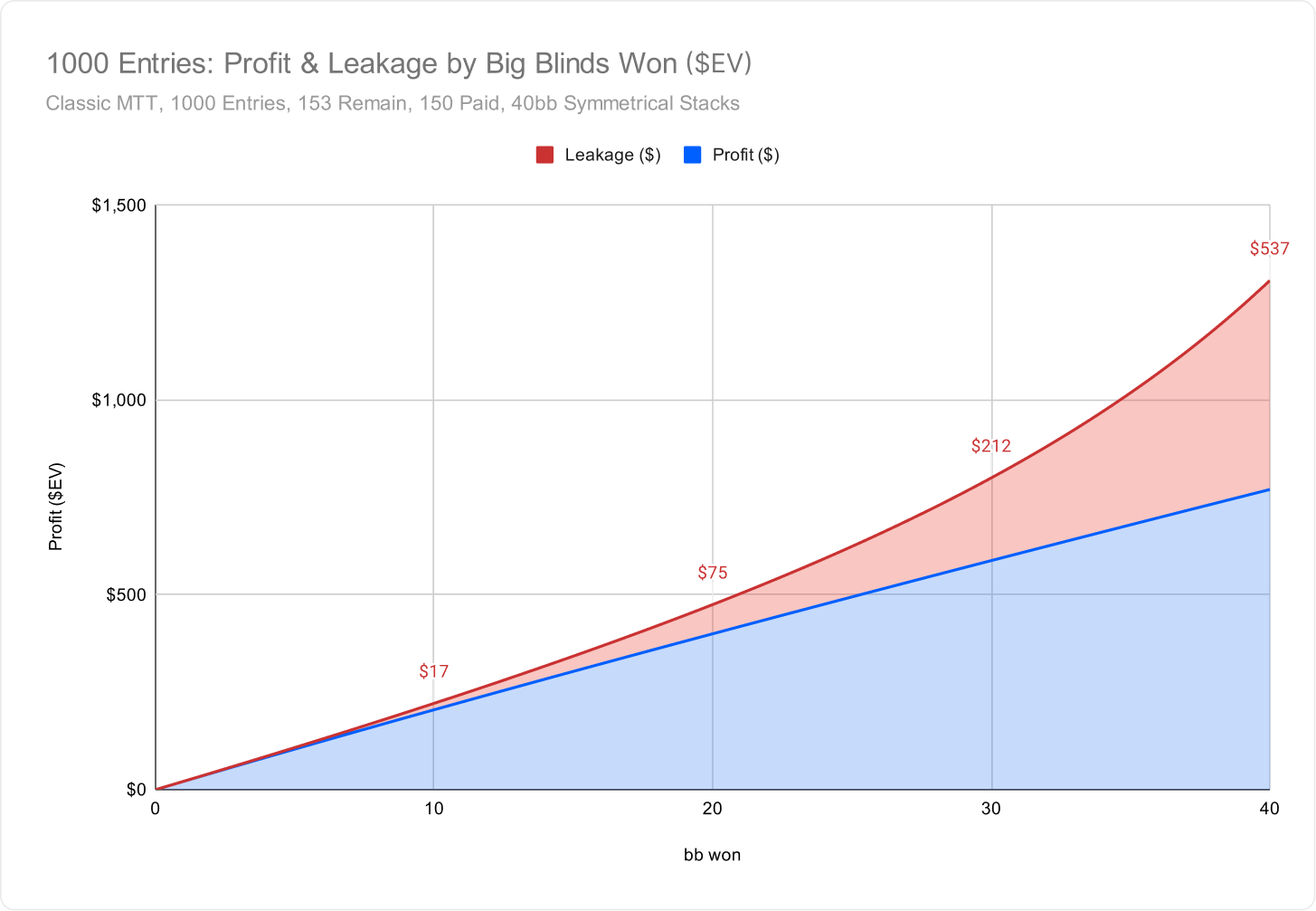
The following graph compares your tournament equity ($EV) profit and leakage as you win chips from your opponent:
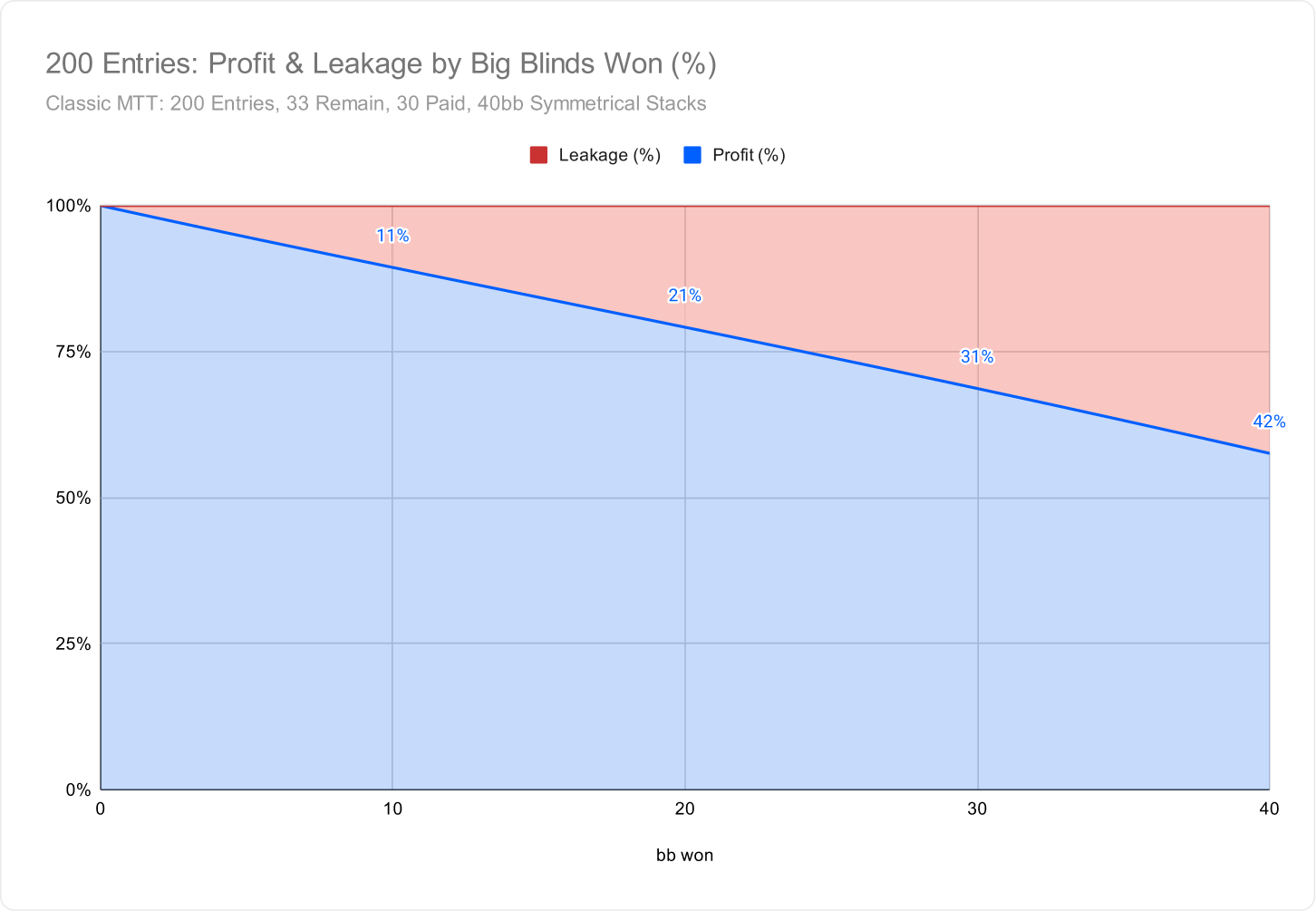
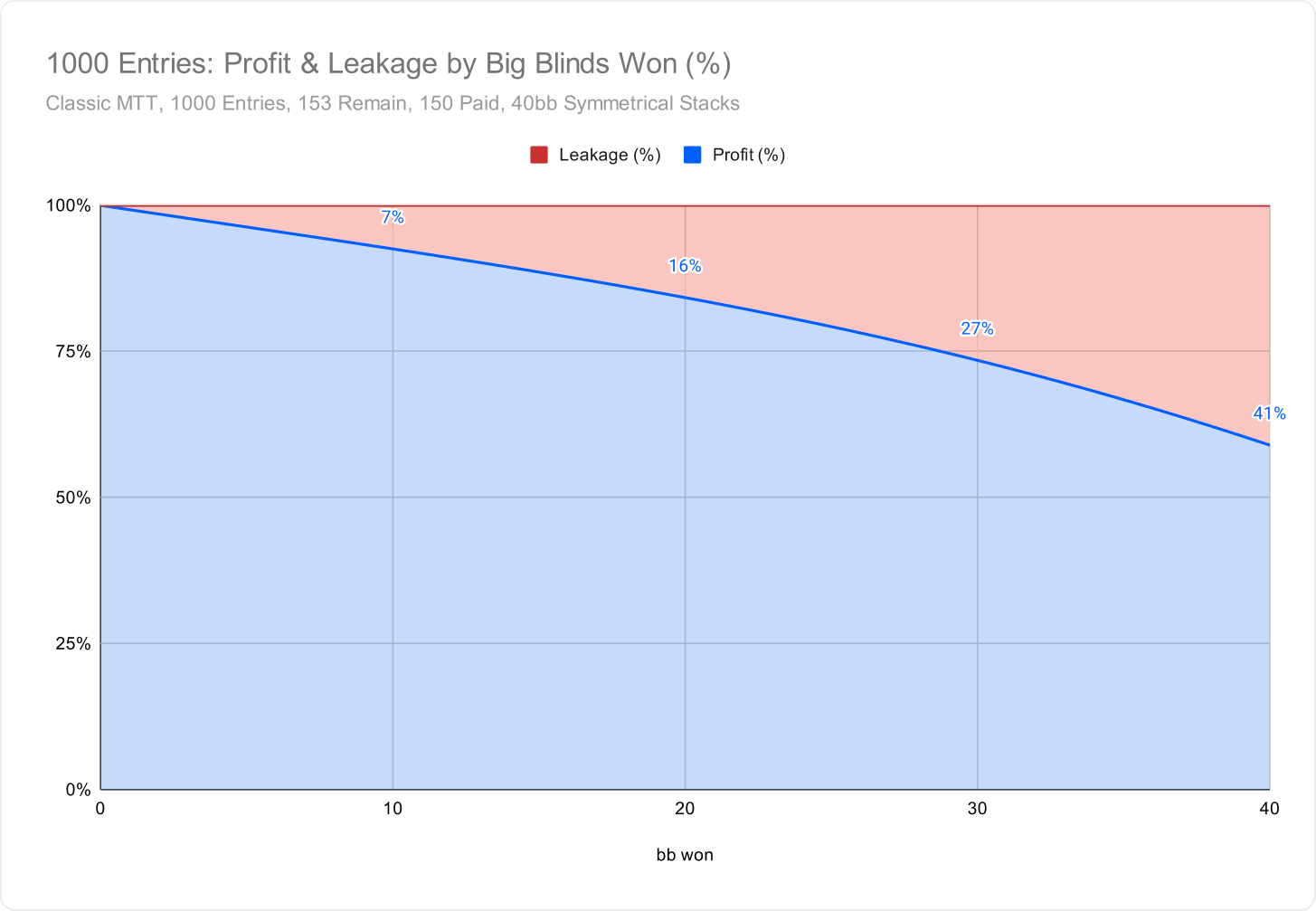
To put that into perspective, we can view this as a percentage (%) instead. This chart displays how the losing player’s $EV is distributed between Hero and the rest of the field:
At the extreme, if they are knocked out, you would gain 58% of their $EV, and the remaining 42% of their $EV is distributed evenly among the rest of the field (31 other players).
We also ran the same experiment for a 1000-entry bubble spot, however the results were almost identical.
We ran the same calculation for a 1000-player tournament:
- $200 buy-in; $200,000 in prizes remaining
- 40bb symmetrical stacks
- 150 places paid; 153 players remaining
- Standard GTO Wizard prize structure
Surprisingly (or perhaps, unsurprisingly), the results didn’t change much. The leakage, in terms of both dollars and percentages, is about the same as in the 200-player case. This spot is technically closer to the bubble in terms of % of field remaining, but the risk premiums are virtually identical.
Drainage
So far, we have been solely focused on negative-sum spots. But it would be just as easy to demonstrate the reverse effect, which I’ll call “Drainage.” Instead of Hero and Villain leaking $EV to the rest of the field, they can actually drain it from the other players. This would be an example of a positive-sum spot.
Let’s use the same setup as the previous 1000-entry example, with these stack sizes:
- Hero: 20bb
- Villain: 60bb
- Rest of Field: 40bb symmetrical
You flip all-in against the big stack.
If you double-up, stacks even out, and you’d gain $475 in tournament equity.
The big stack (Villain) loses $400, and the rest of the field (150 players) also loses $75 collectively (~$0.50 per player).
This means you’ve drained $75 from the rest of the field by evening out stacks.
In essence, what’s happening here is that the rest of the field was rooting for you to bust because it would put them closer to the money. Even before the hand started, your initial 20bb short-stack was statistically more likely to bust sooner. By winning the flip, stacks get evened out, and the remaining players are less likely to make the money, and less likely to place higher in the money. By evening out the stacks, you’ve cut into everyone’s tournament equity, not just the player you won chips from.
This is why, as a rule, when stacks get closer to average, you take money from the rest of the field (drainage). When stacks get further from the average, you donate money to the rest of the field (leakage). Note that there isn’t an official name for this phenomenon, so I had to invent new terminology to describe it.
When stacks get closer to the average, you take money from the rest of the field. When stacks get further from the average, you donate money to the rest of the field.
Understanding the concept of leakage is key to interpreting ICM solver results. Regarding $EV distribution, it’s not just “hero vs villain.” It’s “hero vs villain vs field.”
A Physics Analogy
Perhaps another way to understand this effect is through analogy. In physics, the total energy of a closed system is conserved, but individual reactions can either release energy to other parts of the system (exothermic) or absorb energy from other parts of the system (endothermic). Similarly, in poker tournaments, the total monetary value of prizes is conserved. However, the $EV between two players in a pot can shift in a way that redistributes value within the field: exothermic actions leak (release) value to the rest of the field, while endothermic actions drain (absorb) value from the rest of the field.
How a GTO Strategy Can Lose EV Against Mistakes
In a heads-up (HU) Chip EV spot, Nash Equilibrium (GTO) strategies cannot lose EV against mistakes. Your gains are exactly equal to your opponent’s losses, and vice versa. However, ICM breaks this principle. It is possible to play perfect GTO against imperfect opponents and still lose $EV. It reminds me of this famous movie quote:
“It is possible to commit no mistakes and still lose. That is not a weakness; that is life.”
– Jean Luc Picard
Q&A:
A GTO Strategy Can Lose $EV Against Mistakes. But how is this possible? Does this render GTO useless? Does that mean you should focus on exploitative play in tournaments? We’ll run some experiments in a moment, but first, let’s answer your pressing questions:
How is this possible? Again, it comes down to leakage. When your opponents make mistakes against your GTO strategy, they may inadvertently increase or decrease the amount of $EV that is leaked to the rest of the field. Your opponent’s can’t gain EV against GTO, but they can transfer some of your $EV to the rest of the field, or vice versa.
Does this render GTO useless? No. How will you recognize exploitative opportunities without a solid, unexploitable baseline as a reference? There is no such thing as an exploitative strategy without a baseline from which to deviate from. Furthermore, you won’t always (or even usually) have enough information about your opponent’s strategy to exploit them confidently.
Should you focus on exploitative play in tournaments? Yes. ICM limits the utility of fixed GTO strategies. Generally speaking, it is safe to lean into low-variance exploits such as playing too value-heavy against stations. But it is extremely risky to lean into high-variance exploits such as over-bluffing vs a nit. Remember, leakage tends to increase with variance.
Experiment
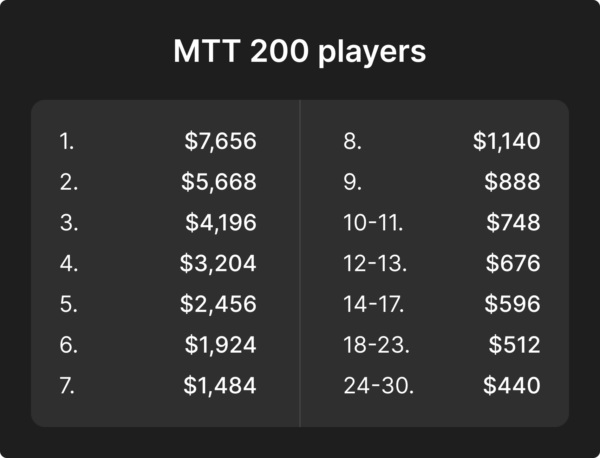
Picture this. You’re on the final table of a massive 1k field MTT. Only three players remain, and you’re one of them. Stacks are 30, 20, 25bb for BTN, SB, and BB, respectively. The payout structure is as follows:
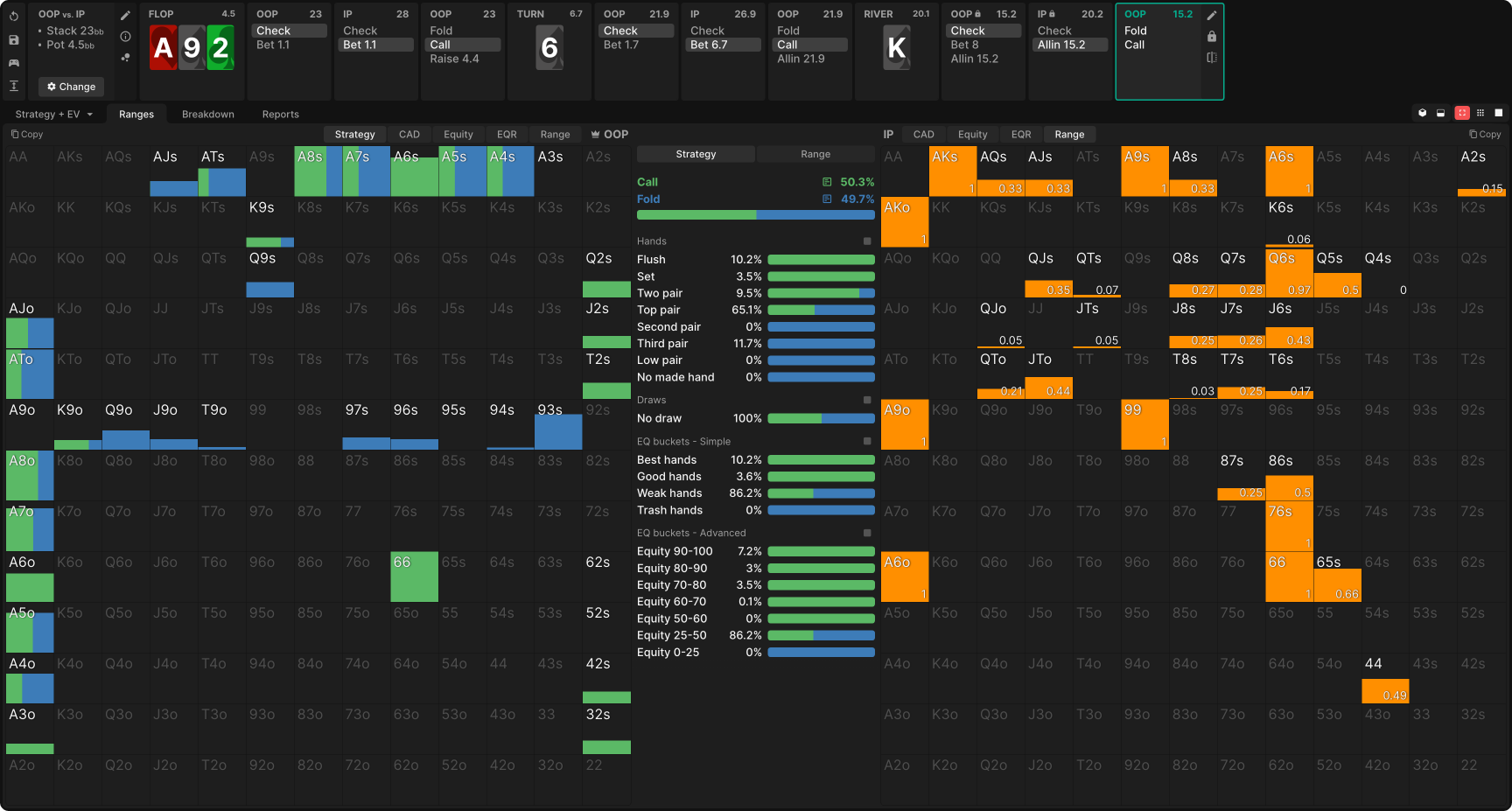
You open the BTN, SB Folds, BB calls, and you triple-barrel-shove on A♥9♠2♣ 6♠ K♠.
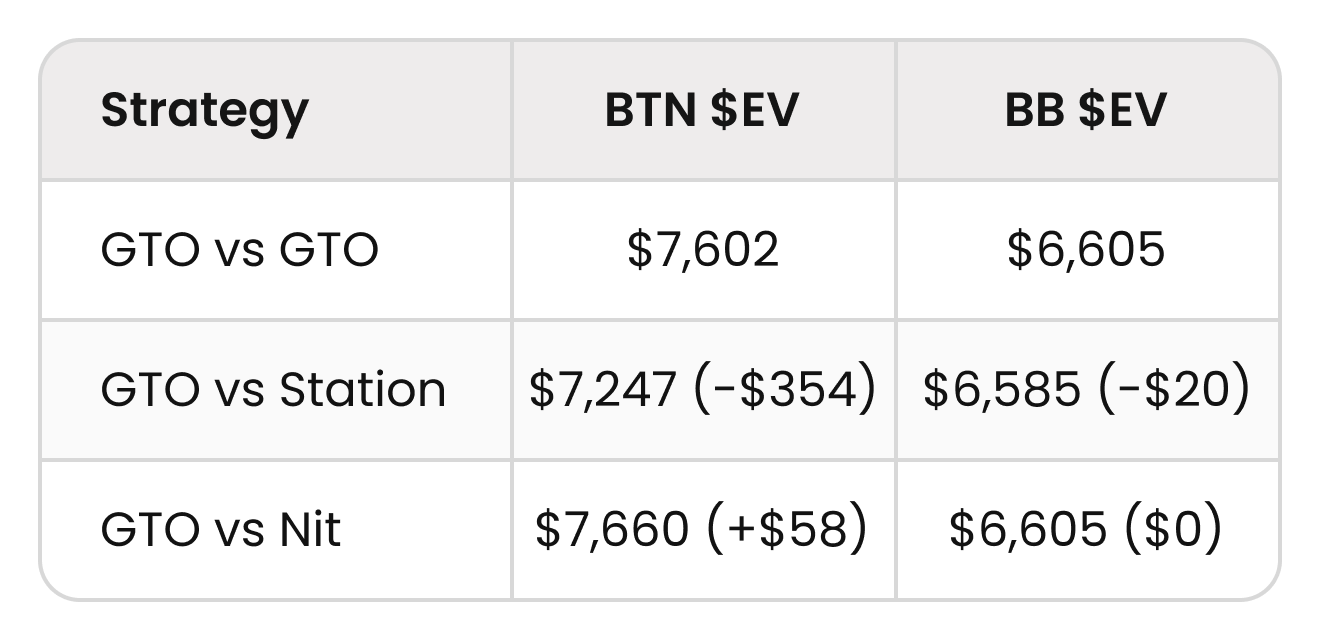
We’ll start with a GTO vs GTO baseline to compare from. Here’s the strategy after shoving the river:
As you can see, BB is supposed to fold many top pairs, even some two pair hands. Overall, they should fold about half the time for your bluffs to break even. Now let’s see how a fixed GTO strategy performs against a non-GTO opponent.
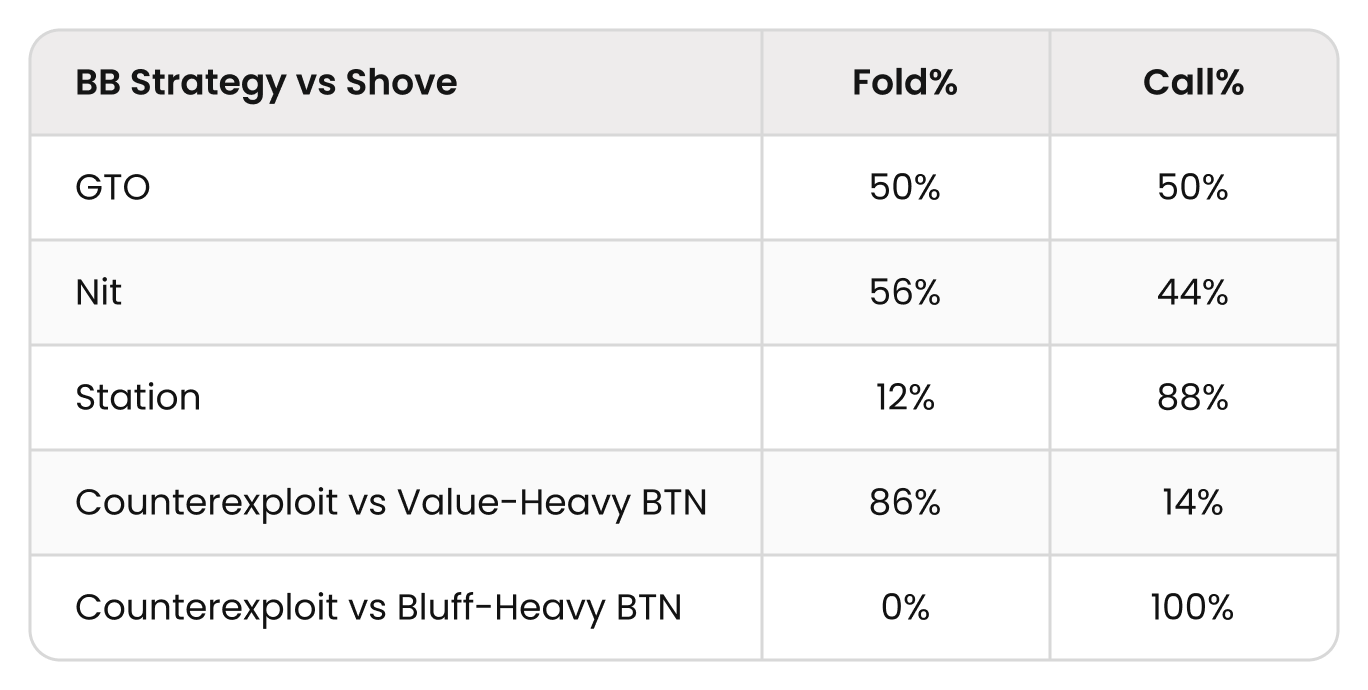
GTO vs Mistakes: The Station and the Nit
- The station calls any top pair or better (this is a ton of calling).
- The nit folds a few combinations of 0EV bluff catchers.
Let’s see how the fixed (unchanging) GTO strategy performs against these two player types:
Players in the Hand
The BTN (who plays a fixed GTO strategy) actually loses a lot of $EV against the station, while gaining a tiny amount of $EV against the nit. Note that the BB doesn’t lose almost any $EV either way. Their station strategy loses $20 because it ends up calling some hands with unfavorable blockers, but this is relatively small. The leakage is leveraged almost entirely on the aggressor!
Rest of Field
Let’s consider this from the point of view of the folded player in the SB. The folded SB’s $EV will increase significantly if BTN or BB stack each other. So any strategy pair that increases the likelihood of this happening favors the SB. The calling station strategy increases this likelihood, thereby increasing leakage. The nit strategy decreases this strategy, thereby decreasing leakage.
Exploits & Counterexploits
BTN doesn’t have to play a fixed GTO strategy. If they know that BB is over- or under-defending, they can adjust their bluffs accordingly. Let’s measure the value of playing an exploitative strategy against the Nit and Station. Furthermore, when doing any exploitative analysis, it is good form to always measure the counterexploitability, in order to gauge the risk and reward of an exploit.
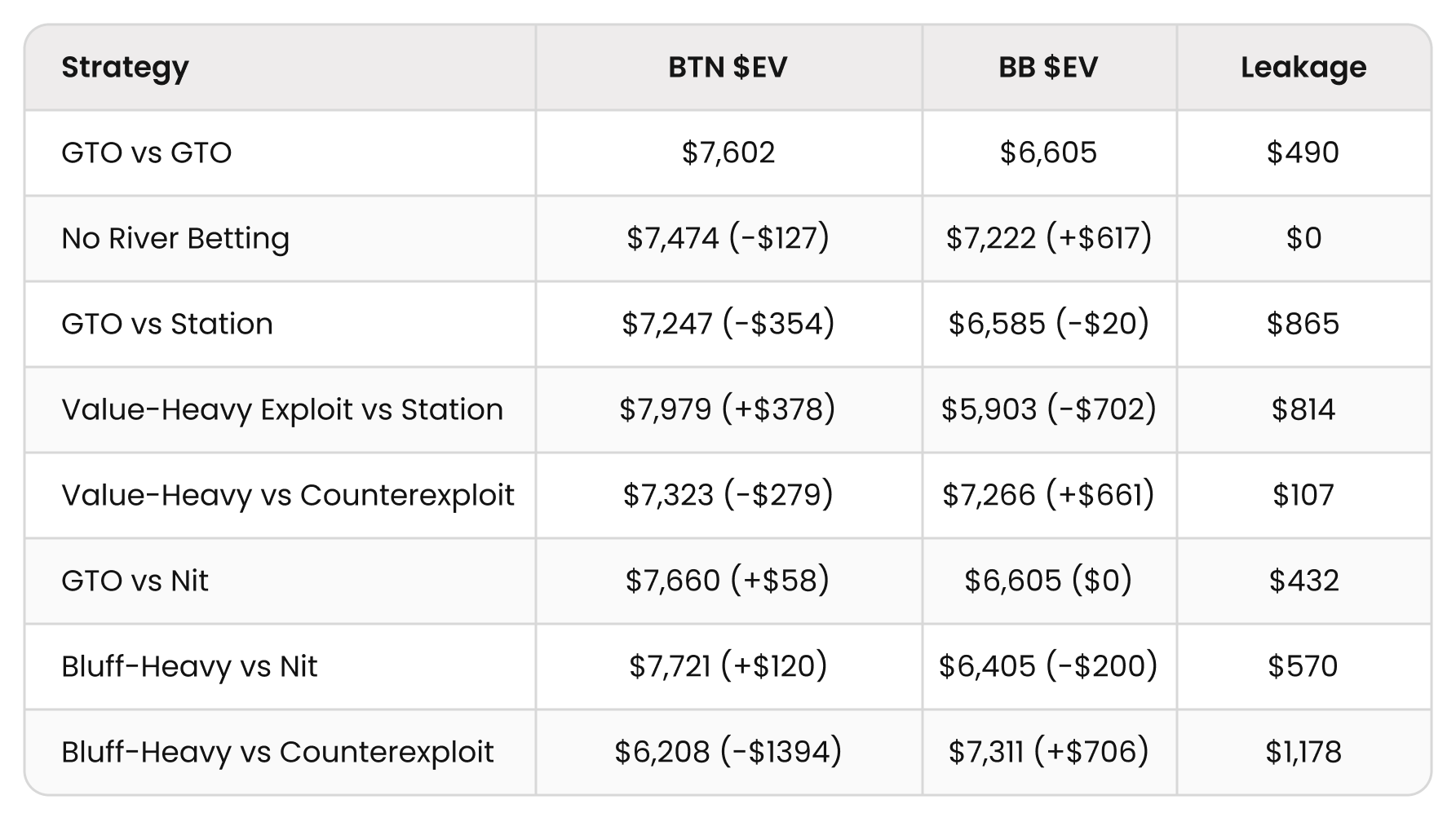
Exploiting the Station
The fixed GTO strategy is already losing (-$354 GTO) against the station due to excess leakage. So we should exploit them. The simplest way to exploit the Station is to just stop bluffing and bet thin for value (+$378 exploit). Of course, they could counter you by over-folding (-$279 backfire).
What’s interesting to note in this case is that even in the absolute worst-case scenario, this value-heavy exploit still outperformed the GTO vs Station strategy. The value-heavy shove makes between $7323–$7979 in the best and worst-case scenarios, while the GTO strategy makes only $7247 against the station.
Exploiting the Nit
The fixed GTO strategy is already gaining (+$58) against the nit due to decreased leakage. But can we get greedy? The simplest way to exploit a Nit is to bluff anything without showdown value (+$120 exploit). However, they could counter by always calling (-$1394 backfire, ouch!)
The problem with this exploit is that it jacks up the variance and leakage, forcing both players to stack each other more often. The risk/reward ratio is terrible. By trying to max exploit the nit, you risk losing $1452 (if they counter) to gain an additional $62 (relative to GTO vs Nit). Your read needs to be correct at least 1452/(1452+62) = 95.9% of the time. If you thought there was even a 5% chance that your nitty opponent would start countering you, then this becomes a bad exploit.
The key takeaway is this:
You should lean towards lower-variance exploits in spots with lots of ICM pressure.
Be mindful of leakage, always remember that their loss isn’t fully your gain—a fat chunk of the reward side of the equation goes to the rest of the field. This is the nature of ICM.
Why Adding Actions Can Decrease EVs
The final way in which ICM breaks Nash is that giving a player more actions (more bet or raise sizes, for example), can actually decrease that player’s $EV! This sounds like it should be impossible. After all, if we added unprofitable actions, that player could simply not use those actions. So, how on earth could giving someone more strategic opportunity decrease their payoff?
To unravel this mystery, I turned to the brilliant Japanese scientist Wataru, a GTO Wizard engineer and the creator of the open-source WASM solver. I asked him to make some toy games that would help me understand this concept.
The underlying reasoning comes down, again, to leakage. In short, by adding more actions to our GTO strategy, we may force the GTO opponent to play more aggressively in response, thereby increasing leakage. As you add more sizings, you give the solver new ways to get money into the pot, possibly increasing the overall aggression of both players.
By adding more actions to our GTO strategy, you may inadvertently force the opponent to play more aggressively in response, thereby increasing leakage.
The Negative-Sum Toy Game
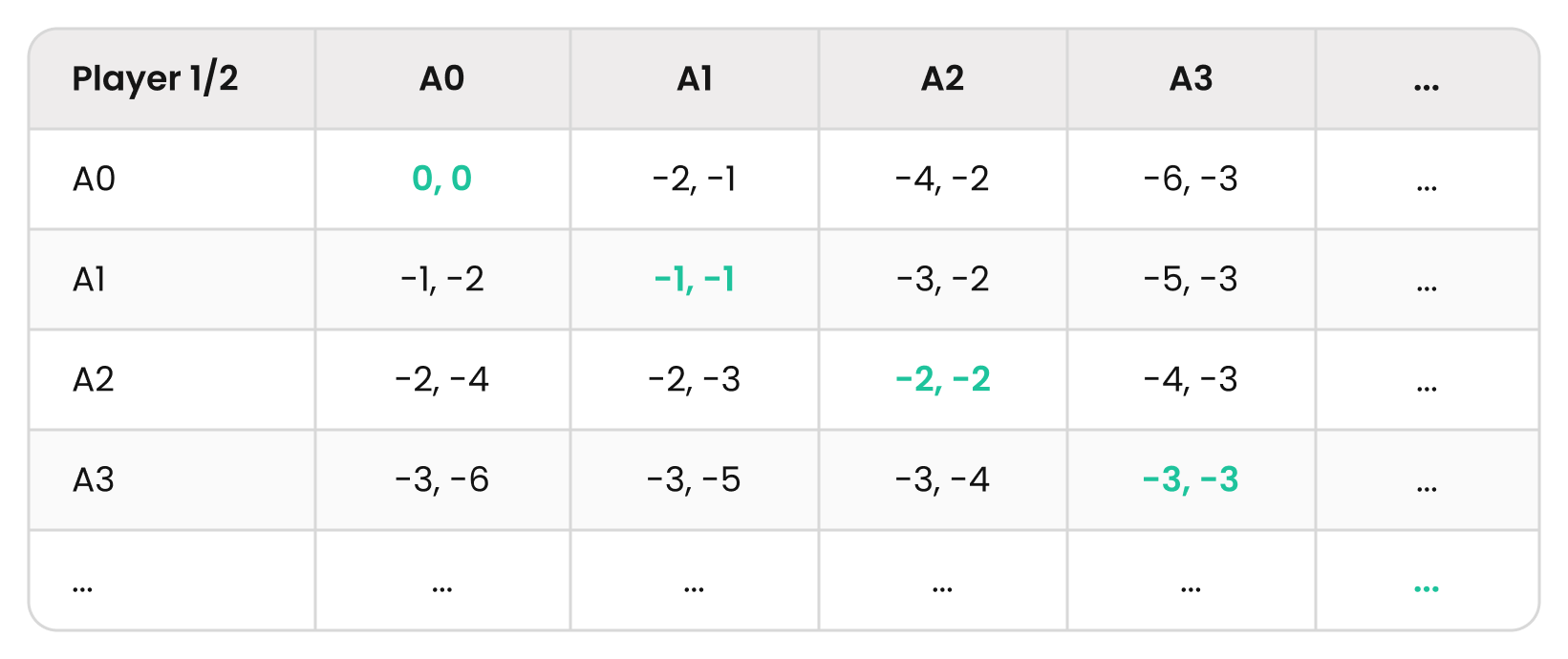
To better understand this concept, let’s examine a negative-sum toy game. Here, each player has actions A0, A1, A2, A3, A… representing how aggressive their strategy is.
The Nash Equilibrium of a more aggressive strategy pair has a greater “EV leakage”, so the EVs of both players decrease. Let’s represent the payoff matrix as follows:
Note that every highlighted diagonal cell is a Nash Equilibrium! Neither player has any incentive to deviate.
Passive (Equilibrium) Strategy Pair
In the best-case scenario, A0/A0, both players make 0. This represents a passive strategy pair (soft-playing). Neither player will take many chips off the other, so less money gets leaked.
Aggressive (Equilibrium) Strategy Pair
Now examine the more aggressive strategy pair A3/A3. Both players are losing -3. They are a lot more likely to stack each other and therefore leak $EV to the rest of the field. However, neither player wants to change their strategy. If you try and soft-play (A0) an aggro opponent, you’d end up with a worse payoff of -6 instead of -3. You’re incentivized to match your opponent’s aggression in this toy game.
Real tournament equities are obviously far more complicated than this simple toy game. However, this negative-sum toy game demonstrates some key concepts:
- There can be multiple Nash Equilibriums.
- Each Nash Equilibrium can have different EVs.
- Minimum EV is no longer guaranteed.
- Your opponent’s mistakes can force you into worse equilibria (imagine a maniac on the bubble).
Example
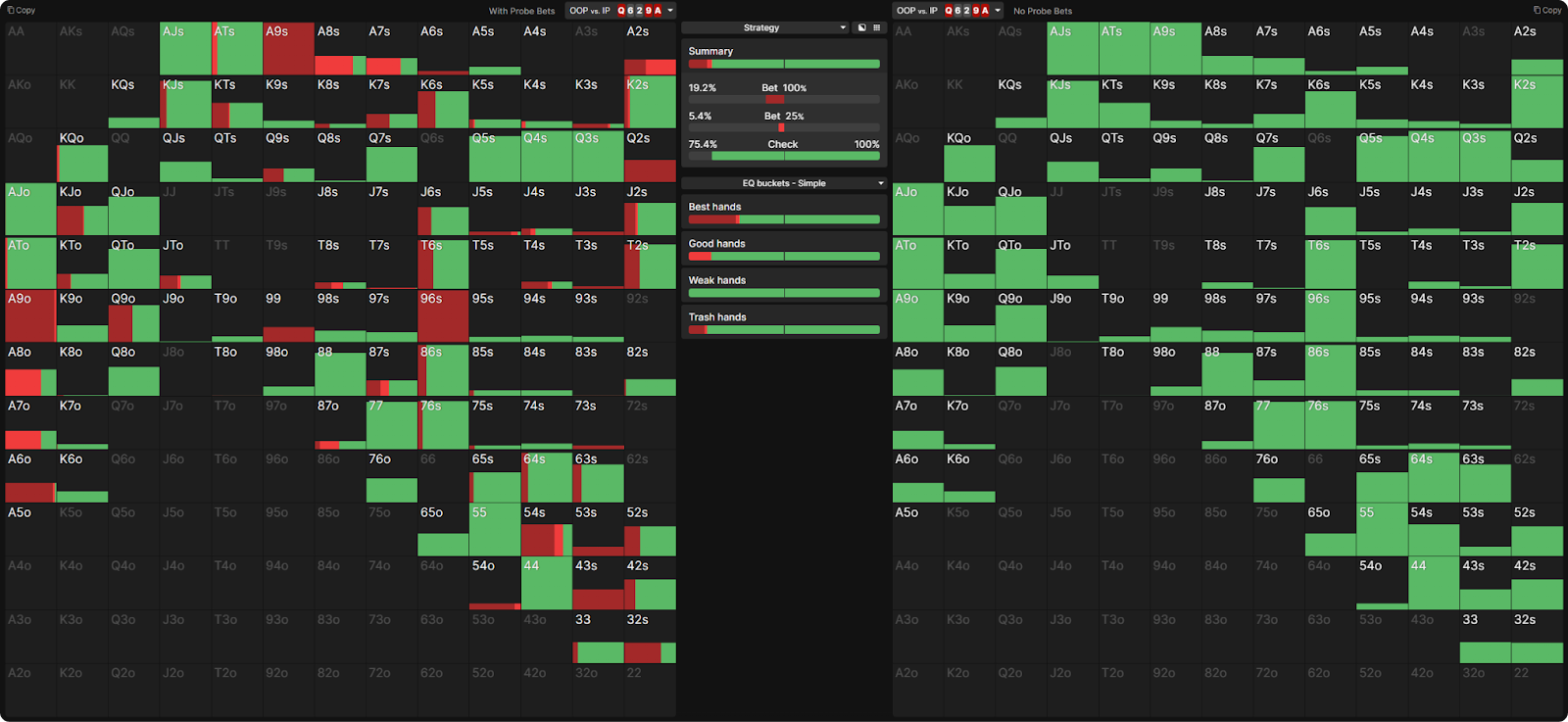
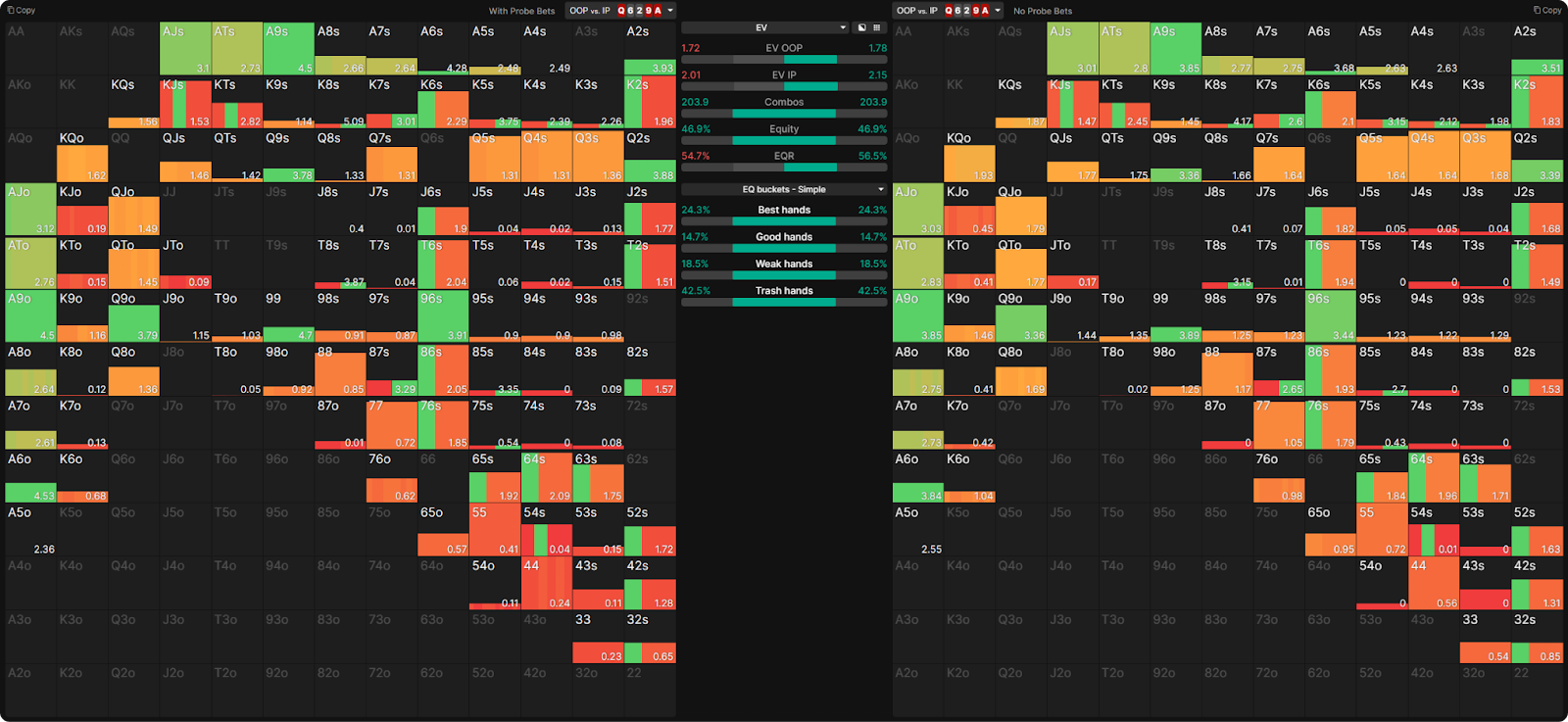
You’re at the final table of a satellite, two places paid, three players remain, 25bb stacks each. BTN opens, SB folds, you call in the BB. The board runs out Q♥6♠2♠ 9♥ A♥, action goes XBC, XX. Action on you on the A♥ river. You have a decision to probe-bet or check.
Let’s compare two possible BB first in river strategies:
- Strategy 1 – Always check
- Strategy 2 – BB has the option to check, probe-bet 25%, 100%, or shove 357%
- IP can bet 40% or shove either way if you check.
First, let’s put these two strategies next to each other to compare:
Now let’s see the EVs:
OK, let me get that straight. We gave BB three betting options to probe river, and their Chip-Scaled Tournament Equity (CSTEChip-Scaled Tournament Equity (CSTE)
—
CSTE is your tournament equity, scaled by the total number of chips in the tournament. For example, if your ICM share of the prizes is 5% and there are 1000 chips in play, your CSTE would be 50.
—
CSTE offers a normalized value that can be compared across different formats and tournament stages. It is especially useful for comparing ICM and Chip EV spots, or comparing $EV to the size of the pot.
—
CSTE = Total_Chips × $EV / Remaining_Prizes) decreased from 1.78 to 1.72?
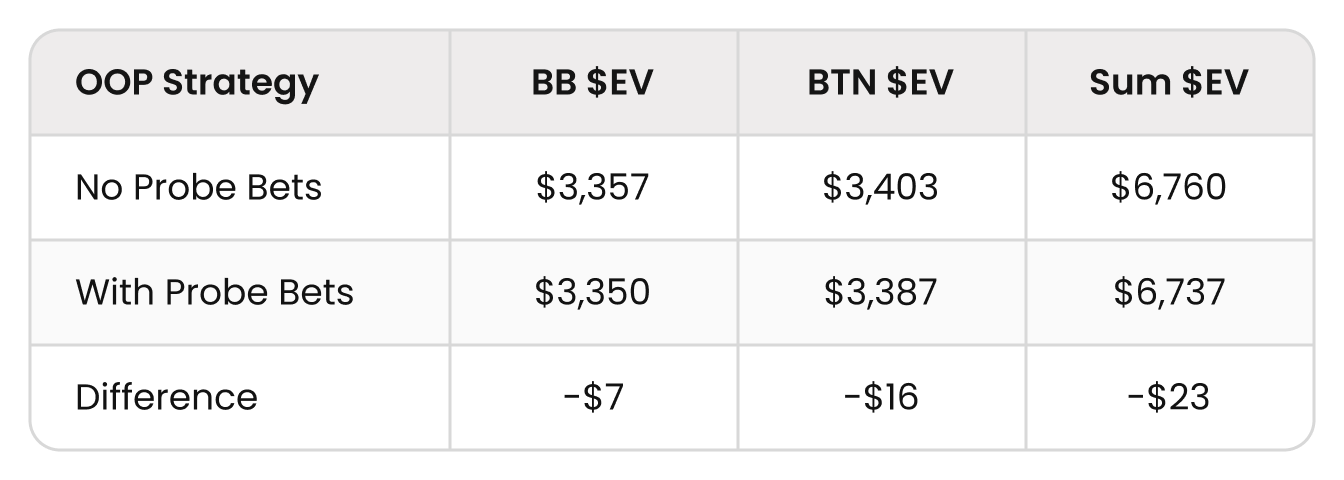
Perhaps a more intuitive way to view EV is to show it with actual dollars. If each of the winning placements were worth $5000, then the $EVs would be as follows:
Note that BB has lost $7. This would never happen in a Chip EV scenario. Giving BB more strategic options would never decrease their EV. However, it can happen in ICM spots.
The reason becomes clearer when you look at the sum of both players’ $EVs. BTN is also losing more money against the probe-betting strategy. What happened here, is that when we added probe-bets, we forced both players into a new equilibrium (arguably, one closer to the true action space). This new equilibrium was more aggressive, increasing leakage to the folded SB.
To be absolutely clear, the probe-bet itself is not unprofitable. If it were, the solver wouldn’t use it. The underlying problem here is that the very threat of a probe-bet forces BTN to play more aggressively, which means BB must also play more aggressively, increasing leakage.
Conversely, when BB is forced to check, they check stronger, meaning BTN checks behind more. But when BB has the option to donk-bet, BTN must bet more often facing a check, or else risk being exploited.
The very threat of a probe-bet forces BTN to play more aggressively, which means BB must also play more aggressively, increasing leakage.
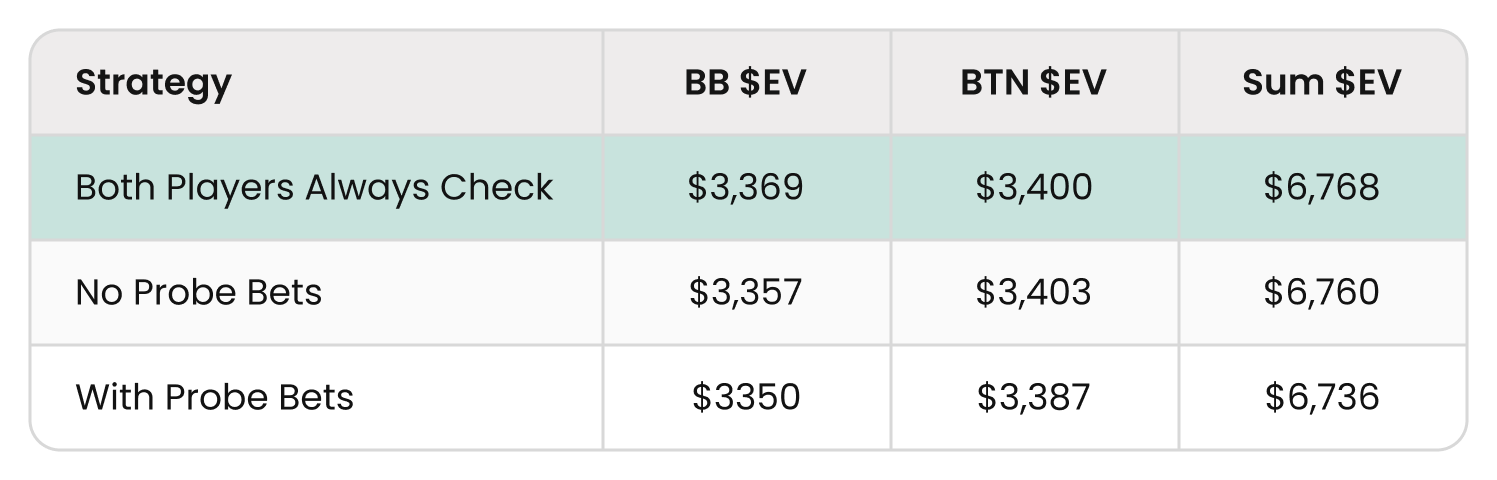
Let’s test this hypothesis by adding one more strategy pair: This time, BTN and BB agree to check down the river.
This is the best strategy pair yet. Note the resemblance to the negative-sum toy game. The more passive strategy pairs have a higher overall payoff in this spot. The more aggressive we allow OOP to be, the more aggro IP must be in response, causing both players to leak more $EV to the folded SB.
In a real tournament, you don’t have this option. Soft-playing is against the rules for good reason. The example above serves only as a warning to help you understand/navigate ICM strategies and the shifting equilibria that may arise from adding or removing betting opportunities.
Summary
Likely, most of you didn’t read this entire article. But if you did, kudos! For the rest of you skim readers, we’ll provide a recap below.
ICM affects the dynamics of Nash Equilibrium due to leakage. In a heads-up Chip EV scenario, your opponent’s loss is exactly equal to your gain. However, in tournaments, this is not the case. Because of ICM, the remaining players in the field can also gain value when you eliminate a player.
First, we explored the key concept of leakage in more detail.
Leakage: Main Takeaways
- When you win a pot in a poker tournament, some of the value goes to the rest of the field due to ICM. This is called “leakage.”
- Leakage means the sum of $EVs in a HU pot is no longer constant. More aggro strategy pairs tend to leak $EV to the rest of the field. More passive strategy pairs tend to leak less $EV.
- Leakage can occur in two ways:
Either by leaking $EV to the field (which I call “leakage”)
Or by draining $EV from the rest of the field (which I call “drainage”).
- When stacks get closer to the average, you take money from the rest of the field. When stacks get further from the average, you donate money to the rest of the field.
Next, we demonstrated how a GTO strategy can lose money against mistakes, and the implications for exploitative strategies.
GTO and Exploits in ICM: Main Takeaways
- Even though exploits become more valuable in ICM spots, a GTO strategy in ICM is important to recognize exploitative opportunities.
- GTO can lose $EV against mistakes. However, mistakes cannot gain $EV against GTO.
- Adjusting aggression can transfer some of the GTO player’s $ EV to the rest of the field, or vice versa. But again, you cannot improve your own payoff against a GTO strategy.
- Generally speaking, exploits become more valuable in ICM spots. It is safe to lean into low-variance exploits, such as playing too value-heavy against a perceived calling station. But it can be extremely risky to lean into high-variance exploits, such as over-bluffing vs a perceived nit.
Lastly, we demonstrated how adding sizes can knock players into new (possibly worse) equilibria.
Why Adding Actions Can Decrease EVs: Main Takeaways
- You generally need to match your opponent’s level of aggression.
- Giving one player more bet sizes can inadvertently lower both players’ $EVs.
- When you give one player more bet sizes, you typically force the opponent to respond more aggressively in kind, which can increase leakage.
Acknowledgements
I would like to give a special shoutout to two of our engineers: Philippe Beardsell (our lead engine developer) and Wataru Inariba (who cracked the new ICM formula), for helping me understand the nature of Nash in non-zero-sum games. At GTO Wizard, we’re proud to employ the best minds in the industry to push the frontiers of poker theory.
Author
Tombos21
Tom is a long time poker theory enthusiast, GTO Wizard coach and YouTuber, and author of the Daily Dose of GTO.
We Are Hiring
We are looking for remarkable individuals to join us in our quest to build the next-generation poker training ecosystem. If you are passionate, dedicated, and driven to excel, we want to hear from you. Join us in redefining how poker is being studied.