How Solvers Work

A Game Theory Optimal solver is an algorithm that calculates the best possible poker strategy. But how exactly do these solvers work? What makes their strategy “the best”?

This article will take a deep dive into how solvers work, what they achieve, and their limitations.

The Goal

Before we dive in, start with these two articles. This article is meant to provide a deep understanding of how solvers work and may feel overwhelming without some basic prerequisite knowledge. If you’re new to solvers, read these first, then return to this article.

As discussed in What is GTO in Poker? And What does GTO aim to achieve? The purpose of GTO is to achieve an unexploitable Nash Equilibrium strategy.

Nash Equilibrium is a state where no player can do better by unilaterally changing their strategy. This means that if each player were to publish their strategy, no player would be incentivized to change their strategy. This is often described as the “Holy Grail” of poker strategies. But that’s not actually what solvers are designed to do. In fact, solvers have no idea what “Nash Equilibrium” means.

Solvers are simply EV-maximizing algorithms.

Each agent in a solver represents a single player. That player has one goal, and one goal only: To maximize money. The problem is the other agents play perfectly. When you force these agents to play against each other’s strategies, they iterate back and forth, exploiting each other’s strategies until they reach a point where neither can improve. This point is equilibrium ☯︎

GTO is achieved by making exploitative algorithms fight each other until neither can improve further.

How to solve GTO

Assign each player a uniform random strategy (each action at each decision point is equally likely).
Compute the regret (EV loss against the opponent’s current strategy) for each hand throughout the game tree.
Change one player’s strategy to reduce their regret, assuming the opponent’s strategy remains fixed.
Go back to step 2, recalculate regret, then change the opposing player’s strategy to reduce regret.
Repeat until Nash.

Each of these cycles is called an iteration. The number of iterations required varies from a few thousand to a few billion, depending on the size of the tree and sampling method.

Step 1) Define the gamespace

Inputs

Poker is far too complex to solve directly; we need to reduce the gamespace using subsets and abstractions to make it computable.

In general, to run a solver, you need to define the following parameters:

The betting tree.
Required accuracy.
Starting pot and stack sizes.
Starting ranges (postflop solvers).
Board cards (postflop solvers).
Postflop card abstractions such as card bucketing or NNs (preflop solvers).
Modifications to the utility function such as rake or ICM.

Betting tree complexity

We need to define the available bet sizes to reduce the size of the game tree. Before we get to the algorithm, we need to understand what a “Betting Tree” looks like. The solver operates within the parameters you provide. If you give a solver a very simple game tree, you produce less complex strategies, but keep in mind the solver will exploit the limitations of your game tree.

The solver will generate a “tree” containing all possible lines within the given betting structure. Each decision point throughout that tree contains a “node”. For example, OOP facing a ⅓ pot-sized bet is a single “node”. The number of nodes in a tree defines how big the tree is. Each node needs to be optimized.

An extremely simple tree like this one has 696,613 individual nodes that must be optimized.

A more complex tree like the type GTO Wizard uses contains ~87,364,678 nodes.

As you can see, complexity grows the tree exponentially. The complex tree above is using 4-5x as many sizes per node, yet it’s 125x bigger and harder to solve. And this is still a major simplification of the true game space.

One of the most difficult problems with solvers is optimizing betting trees to produce solid strategies within the constraints of current technology. We can only make a tree so big before it becomes unsolvable due to its size. We can only make a tree so small before the solver starts exploiting the limitations of that tree. We’re working on algorithms that find simplified betting trees to make it easier to study poker! These solutions will find the best sizes for every spot.

GTO Wizard has many different types of solutions, such as complex solutions with up to 19 sizes and Simple solutions with only a few sizes. Ultimately, we find that it’s better to start with a complex tree, then trim it to a smaller, more manageable tree by removing infrequent lines.

Nodelocking

GTO Wizard plans to add nodelocking and real-time solving in 2023! This powerful feature will be used to explore exploitative strategies and underlying cause > effect principles.

Nodelocking is the process of fixing one player’s strategy at some node in the gametree. We force that player to play a specific way. Nodelocking is commonly used to develop exploitative strategies! For example, if you force it to rangebet the flop, the opposing player will maximally exploit that strategy. It’s important to keep in mind, however, that both players will adjust before and afterwards to accommodate that locked node. Turn and river strategies will change.

If you force a solver to play badly, it will course-correct prior and later nodes to minimize the damage.

The process of locking a single node and letting the solver work around that deficit is known as a “minimally exploitative strategy”. We are not modeling some leak throughout the entire tree, but rather, just a specific point in the tree.

More complex nodelocks are possible. For example, some solvers let you lock the strategies for specific combinations at one node (while letting other combos adjust their strategy). It’s also possible to lock many nodes to recreate and exploit larger trends in your opponent’s strategy – but modern tools don’t accommodate multistreet nodelocks effectively.

Step 2) Solve the game tree!

So we’ve defined the game tree. Now it’s time to solve it! First, we need to understand how solvers calculate the expected value of strategies.

How do solvers calculate EV?

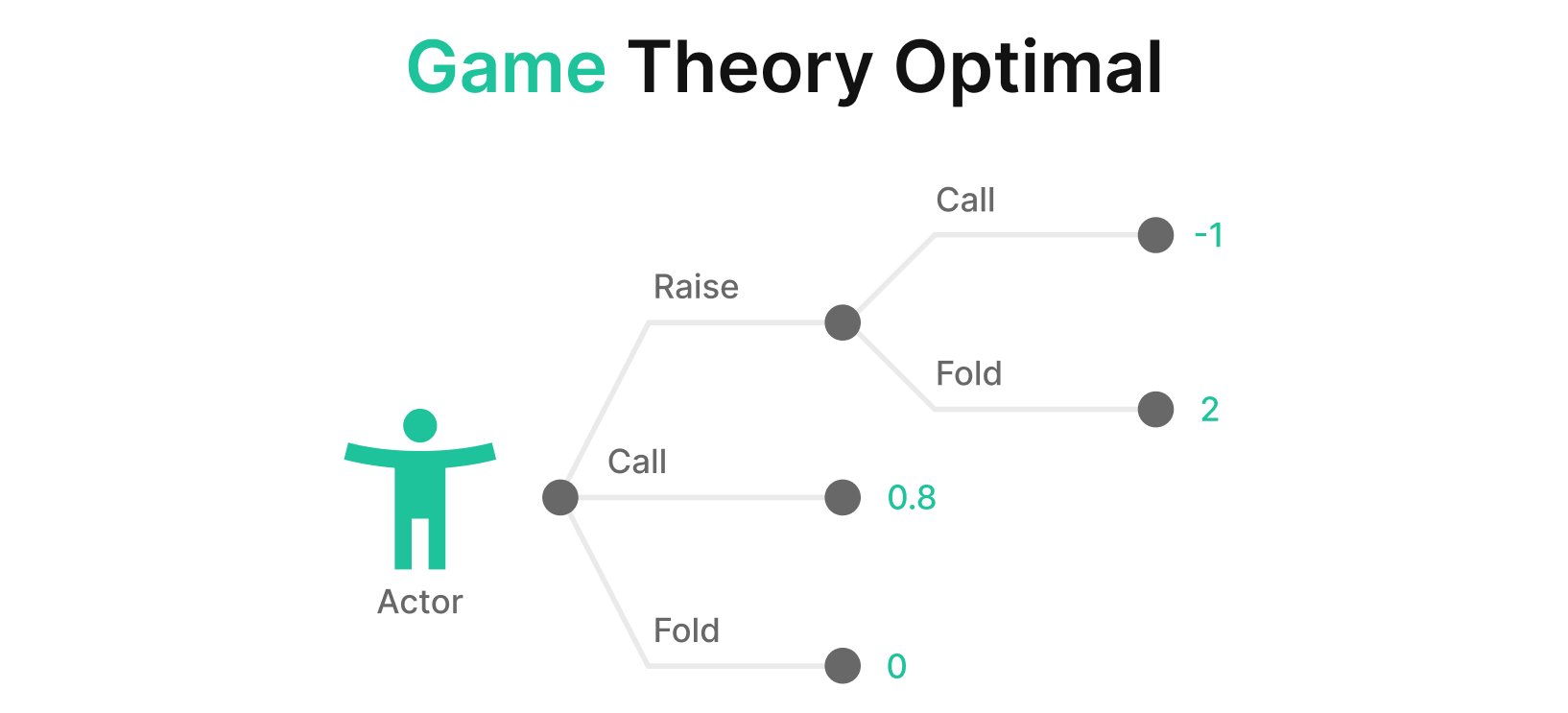
Let’s picture the game tree above. Each dot represents a node or decision point. How do we know how much EV each hand generates at each node?

The process is simple (for computers). Firstly, we define the terminal nodes (AKA leaf nodes). These are points where the hand terminates, either because someone folded or because the hand went to showdown.

Each terminal node is assigned a probability (p) and a value (x). Each hand (i) in our range generates a separate value and probability of reaching each terminal node. We multiply the value and probability of each terminal node and sum them to find the total expected value. The value of each node is defined as the total pot we win minus how much we invested into that pot

Start with a strategy pair.
Based on our strategy and our opponent’s strategy, our hand will reach each terminal nodes this often (p).
The value of each terminal node is x.
The sum of x*p for each terminal node gives us our expected value (EV).
Do this calculation for every single hand at every single node.

E [X] = Σx_ip(x_i)

x_i = The values that X takes
p(x_i) = The probability that X takes the value x_i

Solvers can make this calculation almost instantaneously. Before solvers came along, programs like CREV were used to calculate EV. The limitation being that users had to define the strategies at each node. So typically, we reduced later nodes to pure equity calculations, which was extremely inaccurate.

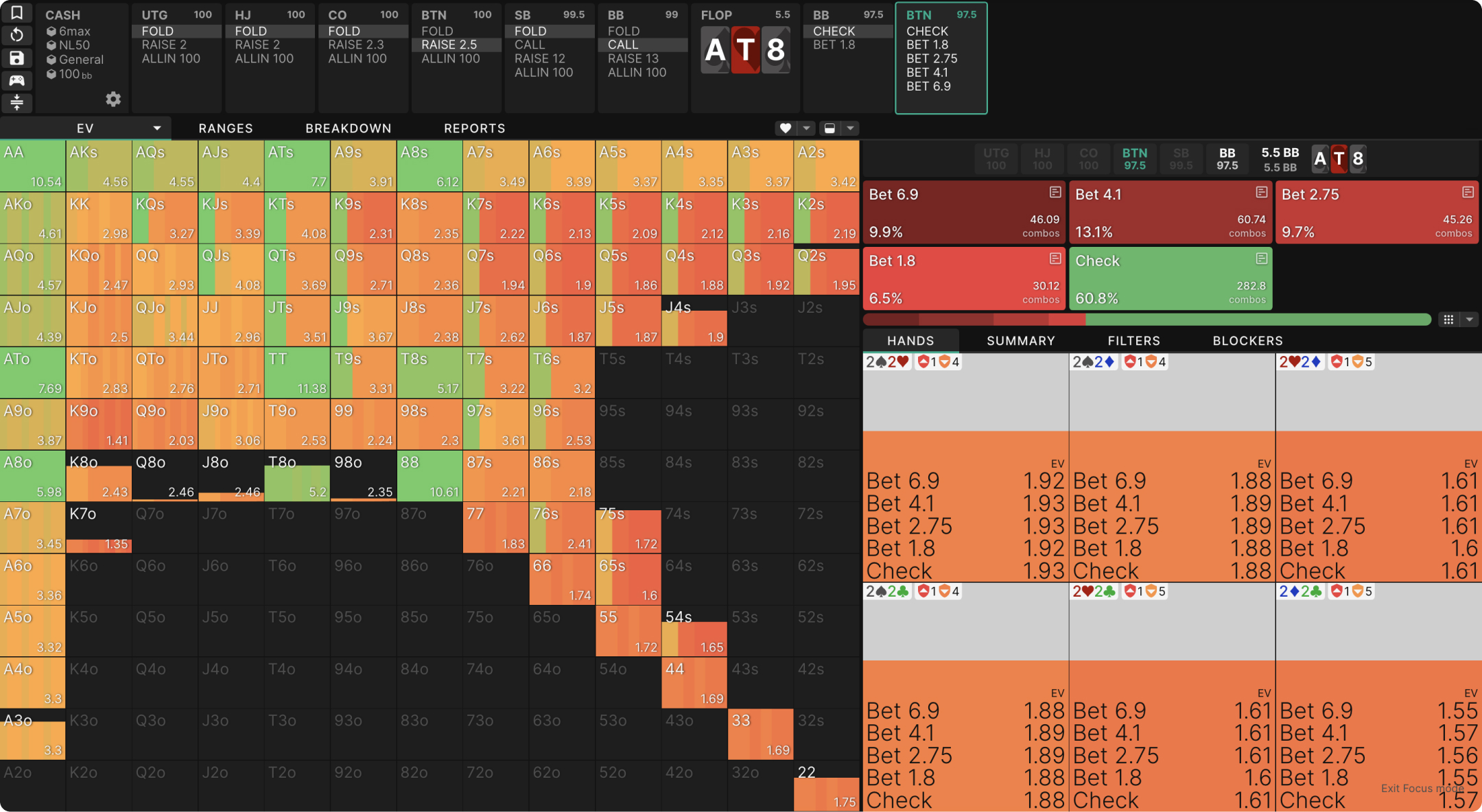
We can observe the expected value of every hand at every point in GTO Wizard. For example, here’s a BTN vs BB SRP in a NL50 cash game. We can see the overall expected value of each hand (use the strategy dropdown), and hovering over any individual hand reveals the EV of various actions we could take:

Regret

Start by assuming our opponent’s strategy is fixed (unchanging). Then run the EV calculation described above for every potential action our hand could take at each node throughout the game tree. Then we select the highest EV decision at each point and work backward from the terminal nodes to calculate the EV of different actions from the first decision point.

Ok, so we know the value of each hand at each node. How do we improve the strategy? This is where the concept of “regret” comes into play.

Minimizing regret is the basis of all GTO algorithms. The most well-known algorithm is called CFR – counterfactual regret minimization. Counterfactual regret is how much we regret not playing some strategy. For example, if we fold and find out that calling was a way better strategy, then we “regret” not calling. Mathematically it measures the gain or loss of taking some action compared to our overall strategy with that hand at that decision point.

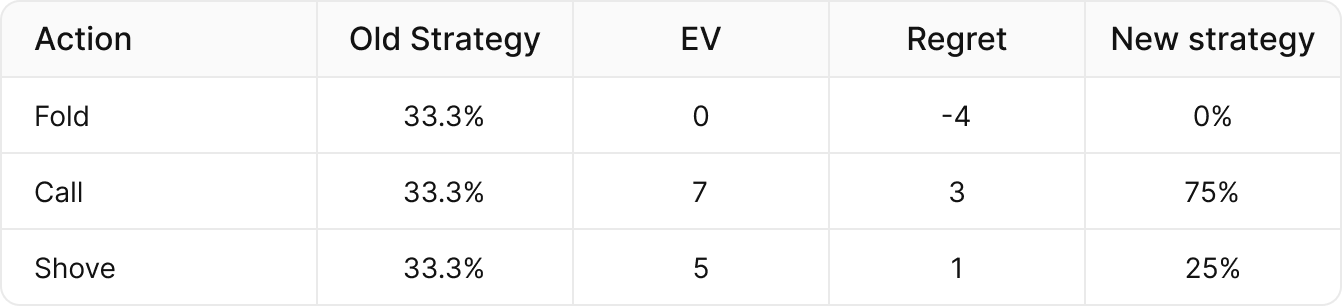
Regret = Action EV – Strategy EV

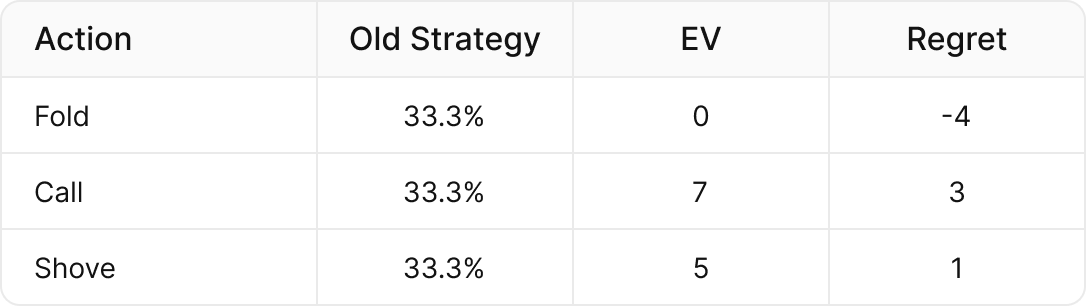
For example, if our current hand’s strategy is to fold, call, and shove ⅓ of the time, and the EV of each of those actions is (Fold = 0bb, Call = 7bb, Shove = 5bb), then the EV of our current strategy is:

(⅓ x 0) + (⅓ x 7 bb) + (⅓ x 5bb) = 4bb

Folding has negative regret, meaning it loses more than our average strategy.
Calling and shoving have positive regret, meaning they outperform our current strategy.

The next step is to change our strategy to minimize regret

The most obvious approach is to simply choose the highest EV action at each decision point with every hand (AKA a maximally exploitative strategy). In our above example, that would mean always calling. The problem is that our opponent can change their strategy, and this can get us stuck in a loop.

For example, Player A under-bluffs the river, player B folds all their bluff-catchers, then player A always bluffs the river, then player B calls all their bluff-catchers, then player A stops bluffing the river, repeating forever. Instead of switching all the way to the best response on each iteration, each player can gently adjust their strategy one step at a time in that direction. This resolves the issue of getting stuck in loops and converges more smoothly when the strategy pair is close to equilibrium.

We can instead use CFR to update our strategy. Let’s return to our previous example. Any actions with negative regret stop getting played. Any actions with positive regret use the formula:

New strategy = Action Regret / Sum of positive regrets

In our example, calling ->3/(3+1) = 75%, and Shoving ->1/(3+1) = 25%, while folding becomes 0% because it has negative regret.

Current Strategy EV = 4.0
New Strategy EV = 6.5

Note that this is just one iteration. As we repeat this process many times, the strategy will approach a point where neither player can improve, achieving Nash Equilibrium.

Accuracy

The accuracy of a solution is measured by its Nash Distance. We start with one question:

How much could player A win if they maximally exploited Player B’s current strategy?

This is easy for a computer to calculate as it already knows the regrets. The difference between the EV of player A’s current strategy and the EV of their maximally exploitative strategy represents their nash distance. The smaller that number, the less exploitable and more accurate the strategies are.

We take the average of all players’ Nash distances to find the accuracy of the solution.

These exact nash distance measurements only work if you’re enumerating the entire strategy each iteration. Most preflop solvers use abstractions and sampling methods which render these calculations impractical and inaccurate. Solvers like HRC or Monker estimate convergence by measuring how much strategies/regrets change every iteration.

GTO Strategies start to converge at a nash distance below 1% pot. Beyond this threshold, strategies are extremely mixed and tend to be unreliable. Most pros consider anything worse than 0.5% pot to be unacceptable. GTO Wizard solves to an accuracy of 0.1% to 0.3% of the starting pot depending on the solution type. The more complex your game tree, the more accuracy is required to differentiate between similar bet sizes. Similar sizes result in similar payoffs, so more complex game trees with many bet sizes require higher accuracy to converge.

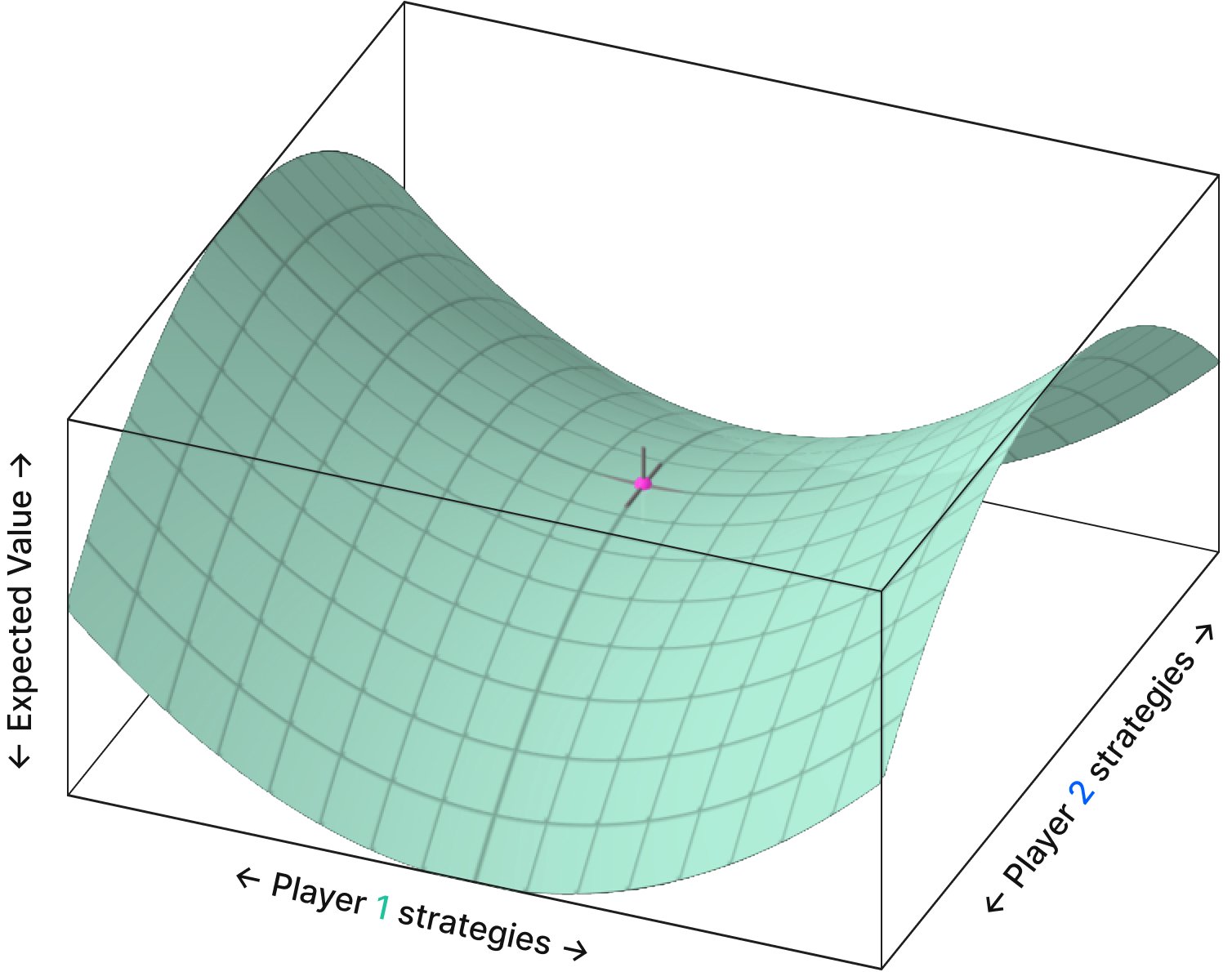
Convex payoff space

How do we know this iterative approach works? Can we get stuck in a local maximum? Poker, in general, can be described as a “bilinear saddle point problem”. The payoff space looks something like this:

Each point on the x-axis and y-axis represents a strategy pair. Each strategy pair contains information about how both players play their entire range in every spot across every runout.
The height (z-axis) represents the expected value of the strategy pair, with higher points representing an EV advantage for one player, and lower points representing an advantage for the other player.

Most solvers use a process called Counterfactual Regret Minimization (CFR). This algorithm was first published in a 2007 paper from the University of Alberta by Martin Zinkevich. That paper proves that the CFR algorithm will not get stuck at some local maximum, and given enough time, will reach equilibrium.

The center of this saddle represents Nash Equilibrium. the point(s) on this graph that have no curvature – meaning neither player can change their strategy to improve their payoff.

Conclusion

Phew, that was a lot of information! Hopefully, by now, you have a much better understanding of how solvers actually work. Let’s recap the main points:

For all practical purposes, the main takeaway is that solvers are EV maximizing algorithms that take advantage of the game tree we provide them.
Solver algorithms generate max-exploit strategies. Pitting these algorithms against each other produces unexploitable equilibrium strategies.
Calculating the expected values of a pair of strategies is the easy part (for computers). Nudging the strategy in the right direction and iterating this process countless times is the hard part.
Poker is too complex to solve directly, so we simplify the gamespace using abstraction techniques like limiting the bet sizes.
Solvers are only as accurate as the abstract game you give them. Too much complexity is impossible to solve and difficult for humans to learn from. Too much simplicity results in the solver exploiting the limitations of that game tree.