How to Solve Toy Games

Toy games are simplified versions of poker that we can use to understand the game theory on a deeper level.

Poker is a complicated game. It’s impossible to calculate GTO strategies on the fly. By reducing it to a toy game, we can solve it by hand, and learn the fundamental incentives of game theory optimal poker.

This article is just an introduction that will cover some of the basics to get you started.
Learning these games won’t turn you into the next Linus. But they will indirectly improve your poker ability by helping you understand and interpret solvers more effectively.

I’ll cover two versions of the polarized vs. bluff catcher toy game in this article. This serves as an introduction to solving toy games.

The Basics

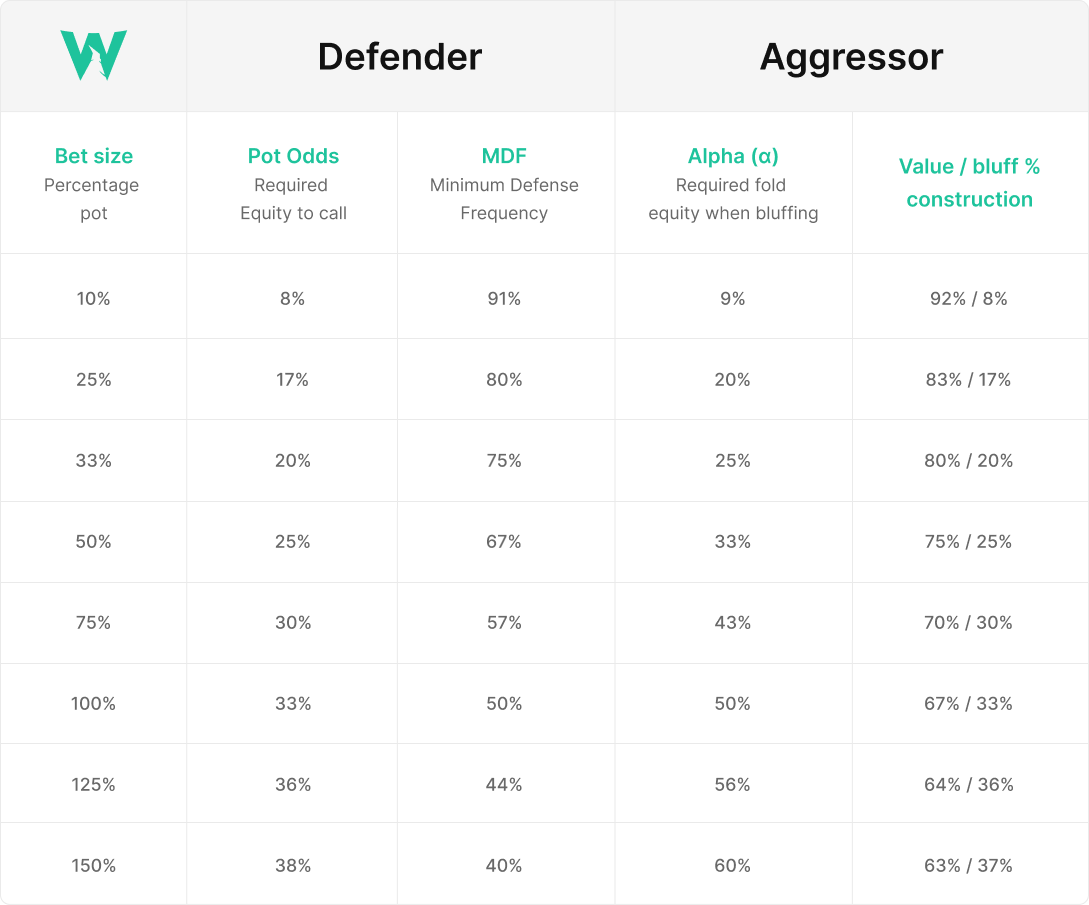
In order to understand toy games, you need to learn a few basic functions such as pot odds, MDF, and how to set up an expected value (EV) calculation.

• MDF tells us how often the defender needs to call to make our bluffs indifferent.
• Pot Odds tell us how much equity the defender needs to call, and informs our bluff/value ratio.
• S = Bet / Pot

Check out these articles if you don’t know how to do that:

{{grid: 3}}

{{/grid}}

Here’s a handy cheat sheet you can use in order to calculate everything quickly⚡

Polarized vs. Bluff Catcher

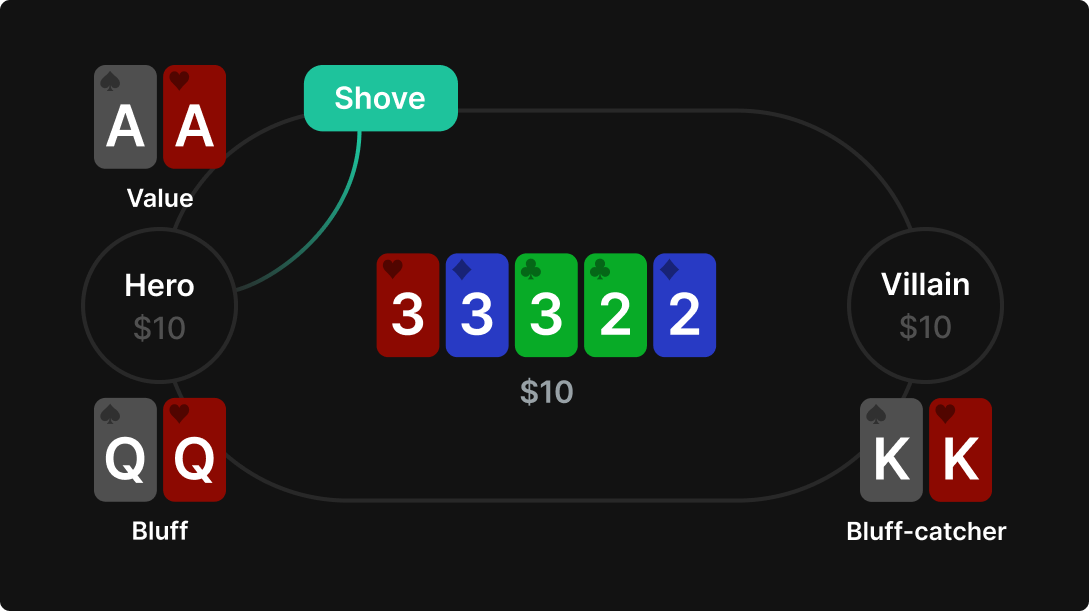
A polarized vs bluff catcher toy game is a situation where one player has either the stone cold nuts, or a complete bluff. The other player has a bluff catcher.

• Player 1 (acts first): Holds either AA or QQ at equal frequency.
• Player 2: Holds KK
• The board is: 22233
• The pot is 10, the stacks are 10. Either player can shove or check

[vc_single_image image=”1566″ img_size=”full” alignment=”center” style=”vc_box_rounded” onclick=”link_image”]

This is sometimes called the “clairvoyant game” since player 1 always knows if they are ahead or behind, and KK may as well be face up.

{{question-mark}}

Now how do we solve this game?

{{/question-mark}}

Let’s break it down into 4 steps:

1. Eliminate dominated strategies—figure out “pure actions” with logic.
2. Calculate bluff-to-value ratio using pot odds.
3. Calculate how often the defender should call using MDF.
4. Generalize the equations for good measure.

Step 1) Start by Eliminating Dominated Strategies

If we check, KK will always check behind. It doesn’t make sense for KK to bet as that would simply fold QQ and get called by AA. KK should simply check behind and win against QQ without risking anything. Therefore, AA should always bet!

{{exclamation-mark}}

Slow-playing the nuts doesn’t make sense if the opponent won’t bet.

{{/exclamation-mark}}

Step 2) Calculate Bluff-to-Value ratio

We know AA should always bet. How often should we bluff? If we bluff too much, KK can exploit us by always calling. Too little and they exploit by always folding. So the optimal strategy is to bet in a way that makes KK “indifferent” between calling and folding.

Look at the pot odds laid. This is a pot-sized bet, so villain needs 33% equity to call.

Required equity = (call amount) / (pot after they call) = 1/3

Therefore, ⅓ of our betting range should be bluffs. If we always bet AA, then we need to balance by bluffing QQ half the time. That way, we lay the exact odds needed to give Villain 2:1 on a call, and they can’t exploit us.

Step 3) Calculate How Often KK Should Call

If KK folds too much, we can exploit them by always bluffing. If KK doesn’t fold enough, we can exploit them by never bluffing and just own them with value bets. So their best strategy is to call often enough to make our bluffs indifferent between betting and checking!

This is where MDF comes in. The frequency that they call is a function of our bet size.

MDF = pot / (bet + pot) = ½

So KK should call exactly half the time. They should randomize between calling and folding to avoid being exploited!

{{info-mark}}

You need to call often enough that they can’t run you over with bluffs, and fold often enough to avoid being taken to value town.

{{/info-mark}}

Let’s summarize. AA always bets. QQ bets half the time, and checks half the time. KK calls half the time, folds half the time, and always checks behind when checked to.

Step 4) Generalize It

{{question-mark}}

What if the bet size was different, though?
What if we had more value or more bluffs in range?

{{/question-mark}}

For this toy game, the general solution is a function of bet size.

Let ‘s’ = bet/pot

• Always bet AA
• Bluff QQ often enough to give them exact pot odds
• Call KK according to MDF

Rewriting MDF with s: KK call% = 1/(1+s)
Rewriting Pot Odds with s: Required equity = s/(2s+1)

KK’s equity facing a bet can be written as the percentage of bluffs in the betting range. Set that equal to the required equity to make KK indifferent!

Bluffs / (Value + Bluffs) = s / (2s+1)

Quiz

Pot = 10
Bet = 7
Player 1 has: 5 combos of AA, and 6 combos of QQ
Player 2 has: KK

Take a moment to try and calculate this yourself before looking at the solution!

{{toggle: Reveal Answer}}

Dominant strategies: AA should always bet, KK should always check (if allowed).

s = bet/pot = 7/10 (i.e., we’re betting 70% pot)

Let’s plug 0.7 into the equations:

• MDF = 1/(1+s) = 1/1.7 = 58.8%

KK should call 58.8% of the time facing a bet to make bluffs indifferent.

Bluffs / (Value + Bluffs) = s / (2s+1)

Let’s plug in 5 for Value, and 0.7 for s:

• Bluffs / (5 + Bluffs) = 0.7/2.4

Rearrange and solve:

• Bluffs = 0.29 x (5 + Bluffs)
• Bluffs = 1.45 + 0.29 Bluffs
• Bluffs = 2.058

We should bluff 2.059 out of 6 combinations of QQ.
So, QQ should bluff about a third of the time.

{{/toggle}}

Polarized vs Bluff Catcher With Traps

[vc_single_image image=”1567″ img_size=”full” alignment=”center” style=”vc_box_rounded” onclick=”link_image”]

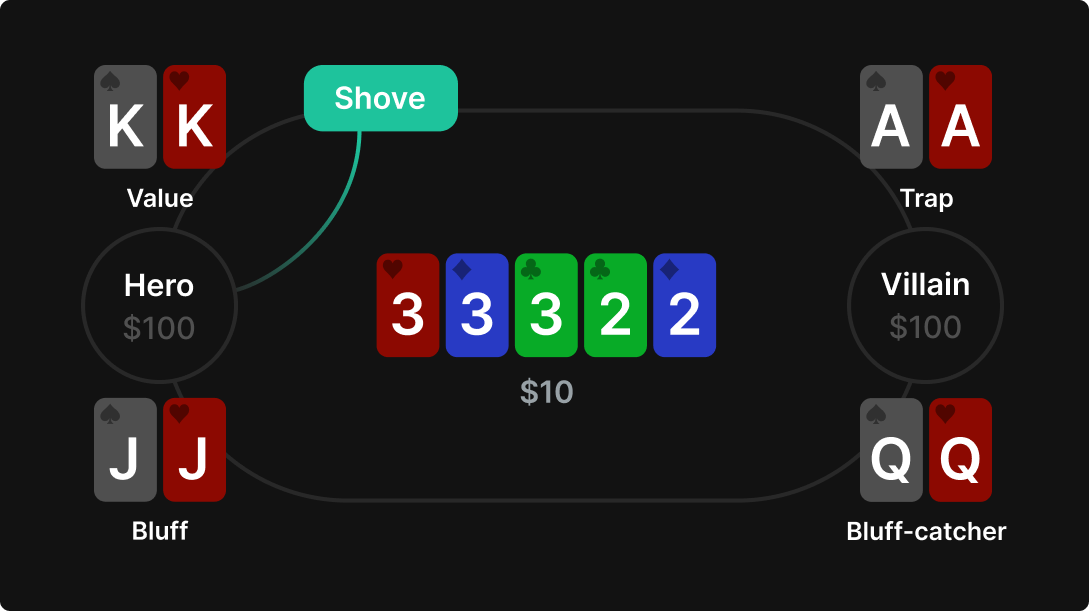
So you know how to calculate the basic polar vs. bluff catcher toy game.

{{question-mark}}

What happens when the defender has traps though?

{{/question-mark}}

The Setup

Villain checks to us on the river (22233). We know Villain’s range is 90% bluff catchers, 10% traps that beat our value bets. We’re in position with 50% value hands, and 50% pure bluffs.

Villain (OOP): 90% QQ, 10% AA
Hero (IP): 50% KK, 50% JJ
The board is: 22233
You can bet any size you like!
Villain can only call or fold.

If Villain didn’t have any traps we could just shove to give them the worst odds possible and make the most money! In this toy game, however, our value hands can be beaten by traps. If we bet too big we donate too much money to their traps. If we bet too small, we don’t extract enough money from their bluff catchers.

The reason I love this toy game is because it demonstrates a fundamental principle of bet sizing theory:

{{info-mark}}

Optimal bet sizing is a function of nut advantage.

{{/info-mark}}

How do we find the “perfect” bet size?🤔

Solving the Toy Game

Let ‘s’ = bet/pot
Let ‘t’ = % of traps in Villain’s range
Let ‘q’ = Hero's equity with value when called
Let ‘c’ = Percentage of time Villain calls

Step 1) Figure Out How Wide They Call

When we bet, they should defend according to MDF. However, their traps will never fold, so we need to make a small modification.

In other words, they defend MDF, but their calling frequency never drops below the percentage of traps in their range (10% in this example).

Because they are defending according to MDF, our bluffs will always be 0EV.

Step 2) Calculate Our Equity With Value Hands When Called

Remember, our value loses to traps, so we need to figure out the equity of our value hands when called, then create an expected value equation.

Our equity when called is a function of bet size. The larger we bet, the more bluff-catchers fold, leaving proportionally more traps in their calling range. Therefore, the equity of our value hands (q) equals the proportion of bluff catchers to traps that Villain calls.

Step 3) Calculate Your Expected Value

We need to figure out an equation that represents our expected value when betting. The optimal bet size will maximize our EV!

The EV of our bluffs is 0 since villain calls according to MDF (although it might be negative if we bet too big, but let’s ignore that). We can skip this part since adding 0 to our EV doesn’t change anything.

That just leaves the EV of our value hands.

That’s a bit cumbersome, so let’s replace this with variables:

• Bet% = s
• Pot = 1 (we’ve normalized the pot since s = bet/pot)
• Call% = c
• Win and lose% = q and (1-q) respectively.

We can take this a step further and substitute q, but this isn’t required unless you want to solve this analytically.

Step 4) Graph the Expected Value by Bet Size

The easiest way to find the optimal bet size is to simply graph the expected value against the bet size and then pick the highest point on the graph!

Play with the graph! I’ve created a simple calculator you can use to graph the EV as we plug in different values for the number of traps. Simply drag the t slider.

[[[!TODO! Reinsert desmos graph]]]

Graphing this function shows that if villain has 10% traps, then our optimal bet size is 123% pot. Although realistically, anything between 100%–150% gives us close to the same EV.

Now some of you may want an analytical solution. To solve that, you’d need to use calculus. More specifically, you’d want to find the argmax ‘s’ that maximizes EV (value bet). Calculus is beyond this video’s scope, and I think simply graphing the EV is much easier.

But for completion:

{{width: 50%}}

{{/width}}

Watch the Full Video!

The full video goes over many other toy games, including:

• Polar vs bluff catcher
• Polar vs bluff catcher with traps
• Bluffing with draws
• Multi-street polar game
• [0, 1] game

[[[!TODO! Reinsert vimeo vid]]]

Further Reading

Learning toy games can be fun while providing you a deep knowledge of game theory that can translate into better play. We’ve only skimmed the surface today.

Check out these books to learn more about how to solve toy games:

• Expert Heads Up No Limit Hold’em, Volumes 1 & 2 by Will Tipton
• Play Optimal Poker, Volumes 1 & 2 by Andrew Brokos
• Modern Poker Theory by Michael Acevedo
• Mathematics of Poker by Chen & Ankenman