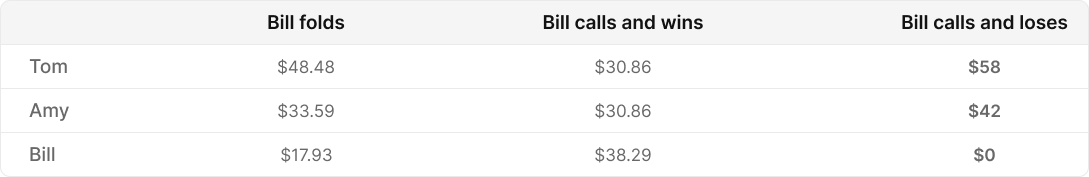ICM Basics
As a tournament player, you may have heard about the concept of “ICM”, but what does this actually mean?
The Independent Chip Model (ICM) is a mathematical formula that converts your tournament stack into a monetary value. This formula was first applied to poker by Mason Malmuth in 1987.
The model uses stack sizes alone to determine how often a player will finish in each position (1st, 2nd, etc.), then assigns tournament equity based on the payouts of those positions.
Tournament equity is your expected share of the prize pool, given the payout structure, your position in the event, and stack sizes.
Table of contents
Why is ICM a thing?
In a cash game, every chip has a monetary value, and the value of chips scales linearly; doubling your stack means doubling your stack’s value.
In tournaments, however, the value of chips doesn’t scale linearly; doubling your stack doesn’t double the value of your stack.
If the value of chips doesn’t scale linearly, we need a method to transform the value of chips into a monetary value. We need to find the real expected value of gaining or losing chips to make strategic decisions. We need a utility function to transform chipEV into $EV.
That’s where the independent chip model comes into play.
How do you calculate ICM?
The Independent Chip Model assumes all players are equally skilled, and therefore the probability of winning is purely a function of stack sizes.
ICM calculates the probability of each player finishing 1st, 2nd, 3rd and so on, then multiplies those probabilities by the payouts of each position.
To calculate the probability of a particular player finishing in 1st, divide their chips by the total amount of chips in play. Calculating 2nd and 3rd positions take more complex math.
Example:
Tom, Amy, and Bill are playing a 3-handed SnG. The stacks and payouts are as follows:
What are the players’ tournament equity?
Let’s start by calculating their 1st place equity. This is the easiest step, as the probability of any player winning is simply their stack divided by the total amount of chips in play. Multiply the probability of winning 1st place by the 1st place prize to get their 1st place equity. There are 1000 chips in play:
Now we need to calculate their equity in 2nd place. This step is more complex, but still doable by hand. To calculate the probability of coming in 2nd, we take the following steps:
- Assume one of the other players wins, remove their chips from play, and divide our chips by the remaining chips in play
- Repeat 1. for every possible 1st place victory
- Multiply each outcome by the probability of the other player’s first place win.
Ok, that sounds complicated, but it’s not so bad. Let’s get started:
2nd place equity: Assuming Tom wins (50% chance)
2nd place equity: Assuming Amy wins (30% chance)
2nd place equity: Assuming Bill wins: (20% chance)
Now we multiply the 2nd place equity by the probability of each scenario:
Total 2nd place equity:
Now we can simply add the first and 2nd place equity together to figure out the total equity:
As you can imagine, this process gets exponentially more complex as we add more players and payouts. Luckily there are plenty of quick and easy ICM calculators online.
It is nearly impossible to calculate ICM during play. The process is far too complex. Tournament professionals build their ICM intuition by studying thousands of ICM spots and playing with variables.
Here’s the same calculation done with a free online ICM calculator (Holdem Resources Calculator):
Tournament Equity
Prizes
How to leverage this information
Let’s ask ourselves how this information can affect the strategy. Amy folds BTN, Tom shoves in the SB, Bill calls in the BB. What will their tournament equity be if Tom or Bill wins? You can calculate this by plugging the resulting stacks into any ICM calculator:
Tom wins:
Tom’s equity is $58 (+$12.82)
Bill’s equity is $0 (-$22.57)
Bill wins:
Tom’s equity is $30.85 (-$14.33)
Bill’s equity is $38.29 (+$15.72)
In other words, Bill is risking $22.57 to win $15.72. Tom is risking $14.33 to win $12.82. ICM has the effect of creating an uneven downside relative to the shortstack. Bill is risking more tournament equity in this situation, so they need a stronger range to defend. This gives the big stack an advantage.
To put it simply, chips won are worth less than chips lost. This uneven risk/reward ratio creates the effect of “risk premium”. You are risking more than a straight chip-EV calculation would suggest.
Total required equity

Let’s use the example above to figure out Bill’s risk premium facing Tom’s shove. We can imagine the blinds are 25/50, with Bill in the BB facing a shove from Tom in the SB.
A simple pot odds calculation tells us how much equity Bill needs to call, in a cash game. We can call this amount the “Chip Equity”.
Tom: 500 chips Bill: 200 chips
Bill needs to call 150 more chips, and their stack will be 400 if they win. 150 / 400 = 37.5%. In a cash game, Bill should call any hand that had at least 37.5% equity against Tom’s range.
But as we know, chips gained do not equal chips lost. Bill needs to weight the cost of a fold against the risk of calling. There are 3 situations, Bill folds, calls and wins, or calls and loses. Here is the tournament equity in each case:
Bill can fold and retain $17.93 of tournament equity. So Bill is risking $17.93 by calling, and will have a stack worth $38.29 if they win.
Let’s do a new pot odds calculation: $17.93 / $38.29. In other words, Bill actually needs about 47% equity to call!
Because of ICM pressure, Bill needed an additional 12% equity. That additional 12% represents his risk premium. This extra risk premium allows Tom in the SB to open much wider, since Bill will always have to overfold relative to his pot odds. That’s the advantage of the big stack.
Risk premium is a variable that’s different for every stack vs every other stack at the table. In general, we can derive the following heuristic:
Your risk premium is higher against stacks that cover you and lower against smaller stacks that you have covered.
General heuristics and effects
It’s not possible to run ICM calculations in game. However, studying these effects off table can greatly help develop your instincts at the table. Here are some of the most valuable heuristics to remember:
- Stack off with a tighter range in tournaments than in cash games.
- Avoid marginal spots. A marginal +cEV spot is usually a -$EV spot in a tournament.
- Medium stacks need to play tighter near the bubble.
- Big stacks can threaten smaller stacks as they take on less risk when stacking off. This is especially true near the money bubble.
- The value of gaining chips is smaller than the value lost when losing the same amount of chips
- Pay attention to the payout structure. Big pay jumps are associated with a higher risk premium.
- When a shortstack is about to bust, resulting in a pay jump, all players except the biggest stacks should generally tighten up significantly.
Limitations of ICM
ICM has some general limitations. It’s a pure math based system that ignores many of the intangible factors of actual play:
- ICM assumes all players are equally skilled. In reality, we’d expect the more skilled players to win a larger percentage of the time, relative to their stack.
- ICM calculations for big fields are computationally difficult. Recent algorithms have made progress in this area, but it’s still very difficult to correctly calculate ICM for large field MTT’s.
- ICM doesn’t consider players’ positions. A 3BB stack is much more valuable on the BTN than in the blinds.
- ICM ignores blinds increasing. If you know the blinds are about to increase, that can affect the optimal strategy, especially with shortstacks involved.
- ICM underestimates the chip leaders’ advantage. Bigger stacks can often bully smaller stacks due to ICM pressure, which leads to a higher win% for big stacks than ICM would otherwise indicate.
Alternative models
Some alternative models exist to address these limitations.
One of the most popular is Future Game Simulation, which essentially is a recursion of ICM. It calculates several rounds in advance to take into account position, blinds increasing, and future play. This model is used in conjunction with regular ICM calculations to better approximate tournament equity, and is considered a staple in most tournament software.
There is also the Dependent Chip Model, which seeks to address ICM underestimating the big stack advantage. Although this model tends to be more complex and overestimate shortstack advantage.
Conclusion
ICM is a complex tool that’s used to transform stacks and payouts into actual tournament equity. Although these calculations are not possible in-game, studying ICM off the table will greatly improve your chances on the felt!
ICM encapsulates one of the most important aspects of tournament play: The value of survival.
Tournaments are not about maximizing BB/100, they are about maximizing your tournament equity. As you explore these concepts, you’ll run into spots where you need to play far tighter than your instincts might otherwise tell you, and other spots where you should play far looser than you anticipate. Learn how to use survival pressure to your advantage, and avoid committing ICM suicide!
Author
Tombos21
Tom is a long time poker theory enthusiast, GTO Wizard coach and YouTuber, and author of the Daily Dose of GTO.