Why doesn’t my solution match GTO Wizard?

So, you’ve got your own solutions to some spot, compared it to GTO Wizard, and noticed that the strategy isn’t the same. So what’s going on here? Shouldn’t you get the exact same results?

This is one of the most common questions we get on the GTO Wizard Discord.

This article will explore how small changes to initial parameters or solver algorithms can drastically change the strategic output.

Compare apples to apples

Before you go comparing solutions, please ensure that you are comparing “apples to apples”.

Ask yourself these 5 questions:

It’s important to realize that small changes to the initial parameters can cause a butterfly effect that changes the solution’s output. Solvers are the embodiment of chaos theory. The first part of this article will explore how different starting parameters can drastically change the strategy.

What if you use the exact same parameters? It may surprise you to learn that different solver algorithms can produce different strategies in strategically similar spots. However, that doesn’t mean one strategy is superior. In fact, strategies that look very different can and often will be extremely close to the same levels of EV and exploitability.

How starting parameters change the strategy

Example 1 – BvB with and without limp

Different preflop ranges result in different postflop strategies. If your preflop ranges are designed for different preflop bet sizes, chances are you aren’t using the same ranges.

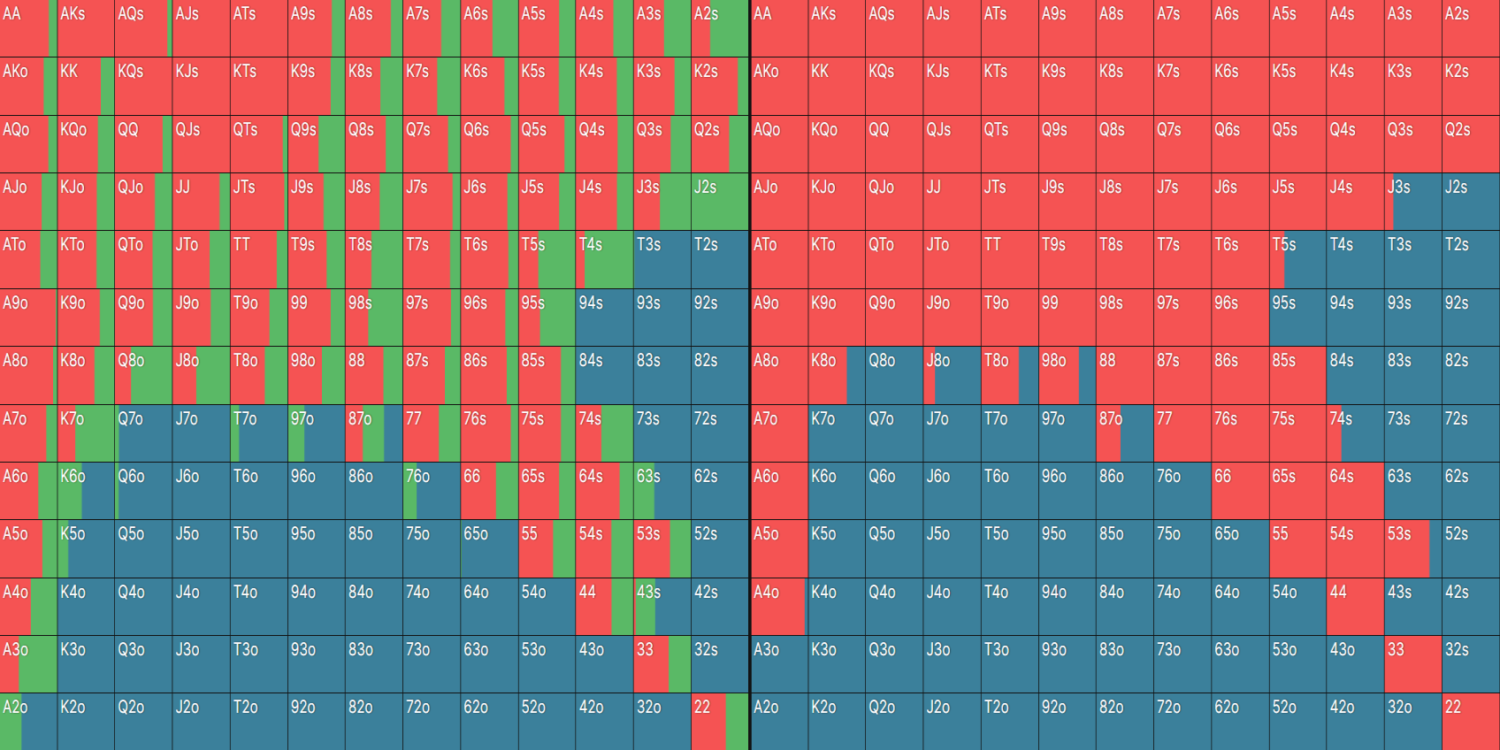
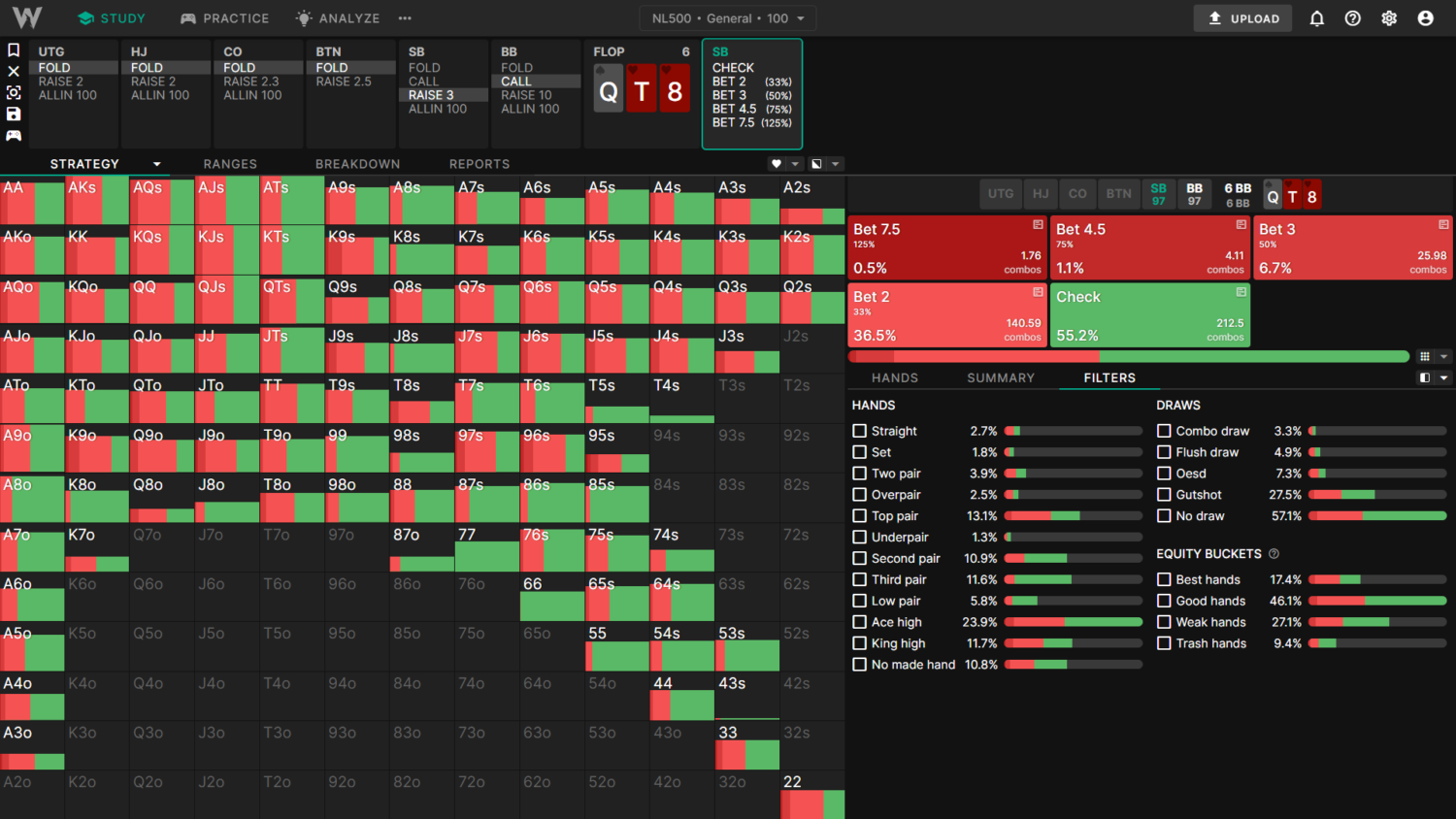
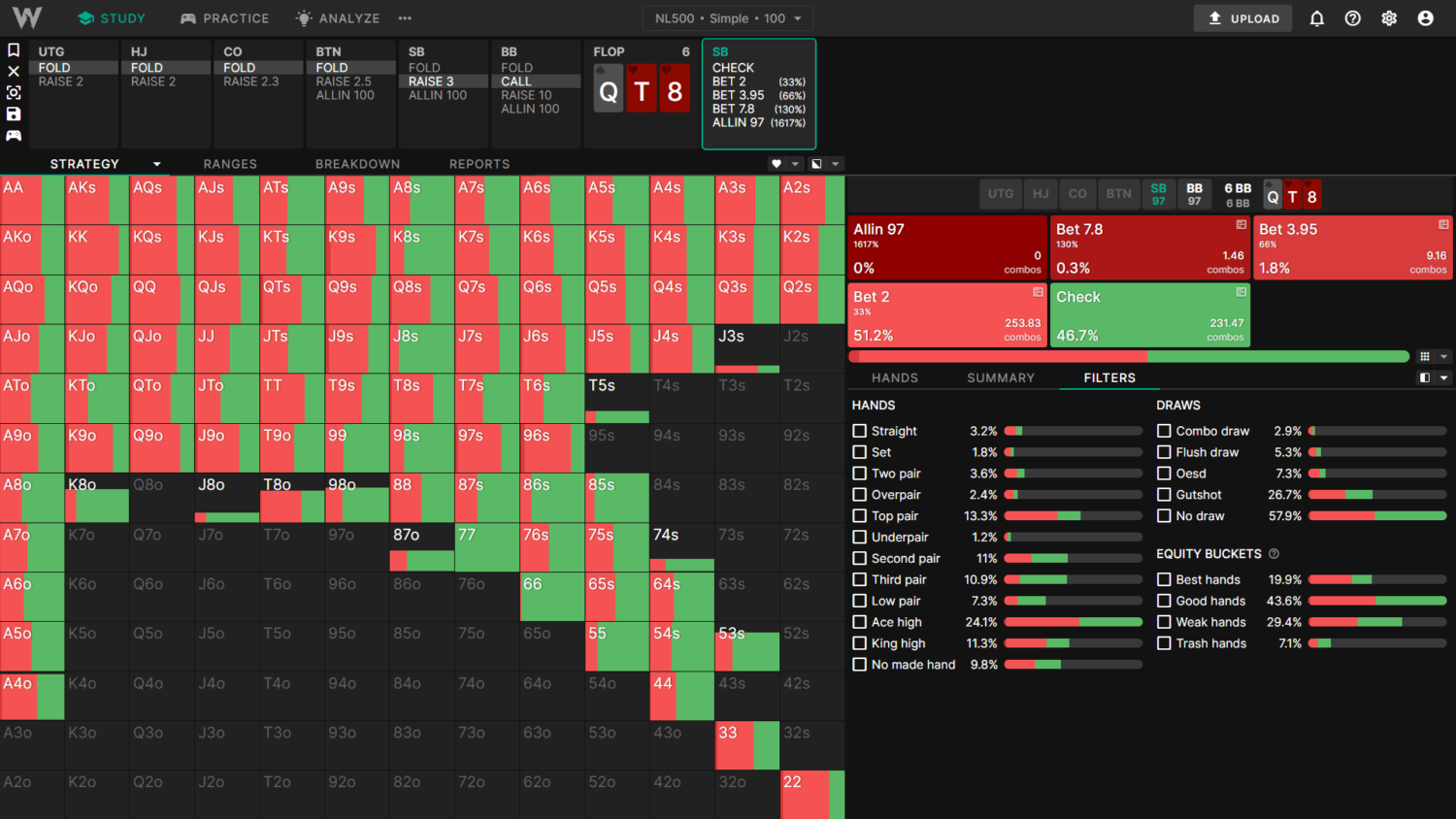
Here’s an example. Let’s compare a SB opening range, with and without limps. On the left we have the General Solution; on the right we have the Simple Solution:

The limping strategy (green) slightly polarizes the RFI. The strategy on the right contains proportionally more medium cards in the 9-T region and slightly fewer low/high cards compared to the opening strategy on the left.

For example, the General solution checks this QT8 flop 55% of the time, whereas the Simple solution (which doesn’t limp and has more middling cards) only checks 46%.

General (With preflop limps):

Simple (No preflop limps):

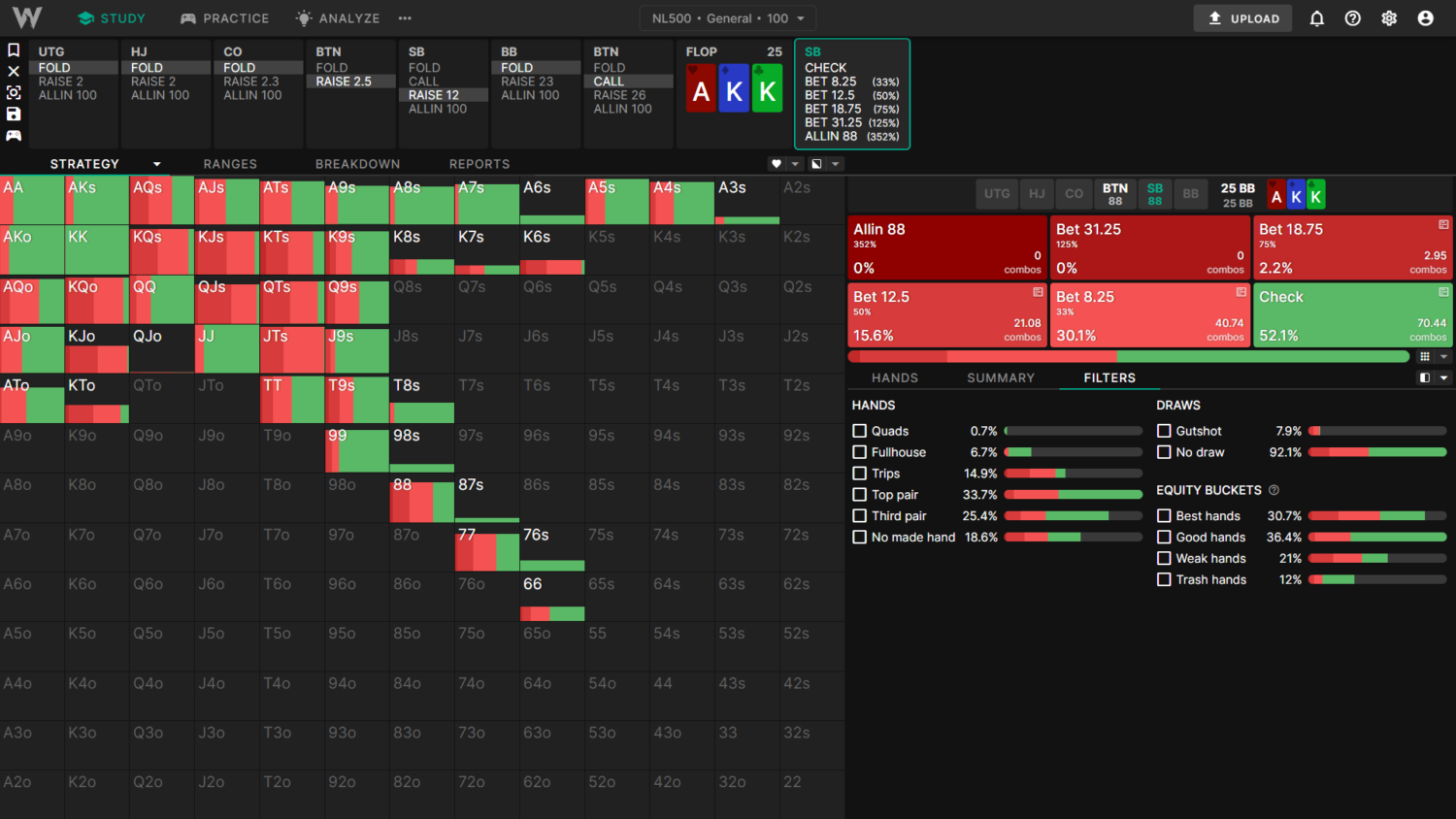
Example 2: SB vs BTN 3BP with different preflop 3bet sizes

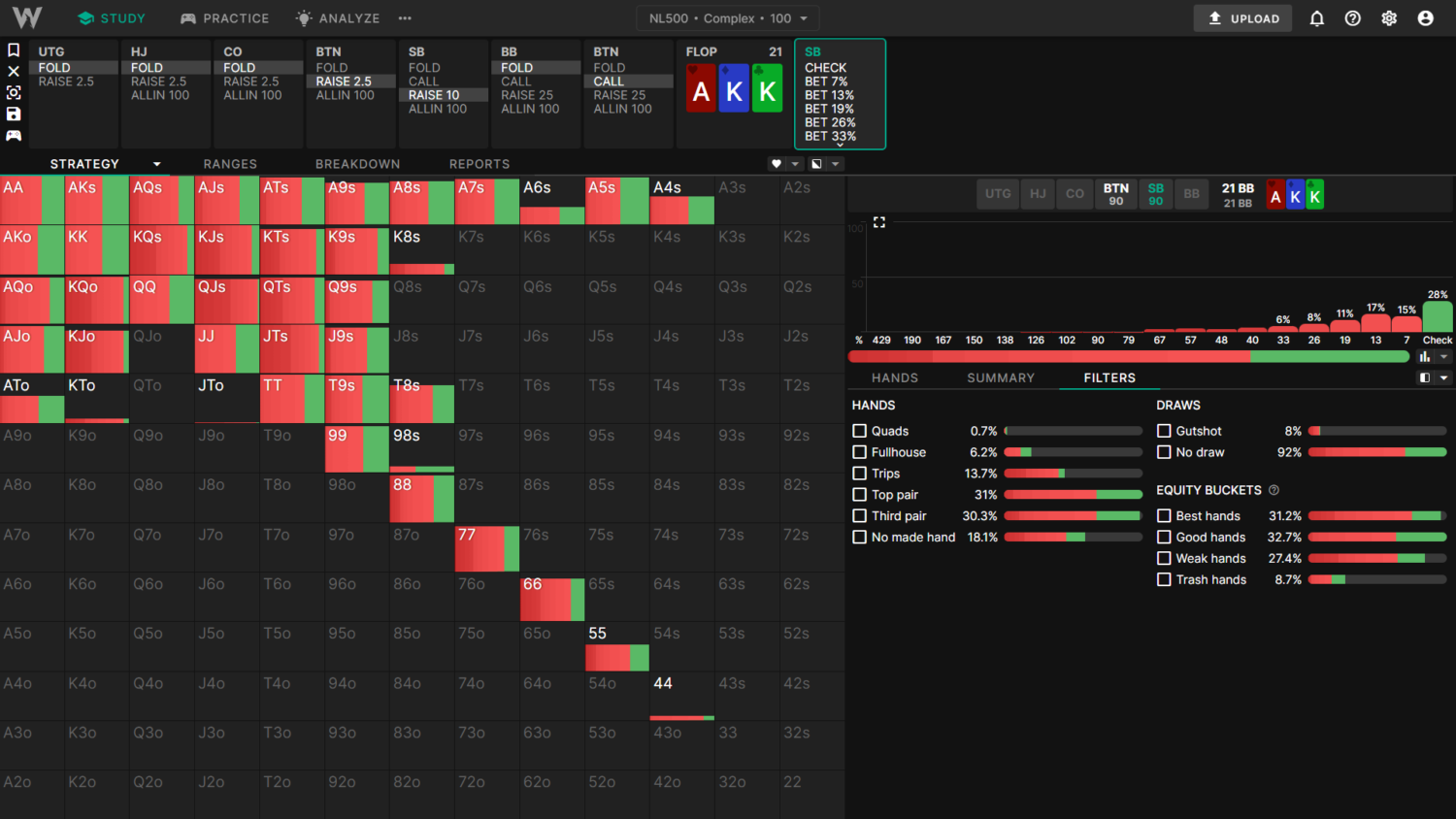
This example will compare the SB flop cbet strategy between the 500NL Complex and General Solutions on AKKr.

The Complex Solutions use a smaller (10BB) 3bet size with a more linear range. The smaller 3bet causes BTN to call wider. Additionally, Complex has many small bet sizes available, which become relevant for this kind of a flop. These factors together mean SB cbets more often (72% cbet frequency) in the complex solutions:

The General Solutions use a larger (12BB) 3bet size with a slightly more polar and top-heavy range. The larger size results in BTN calling tighter. Additionally, the smallest bet size available in General is 33% pot, which leads to more checking. Together, these factors direct SB to check more often (48% cbet frequency):

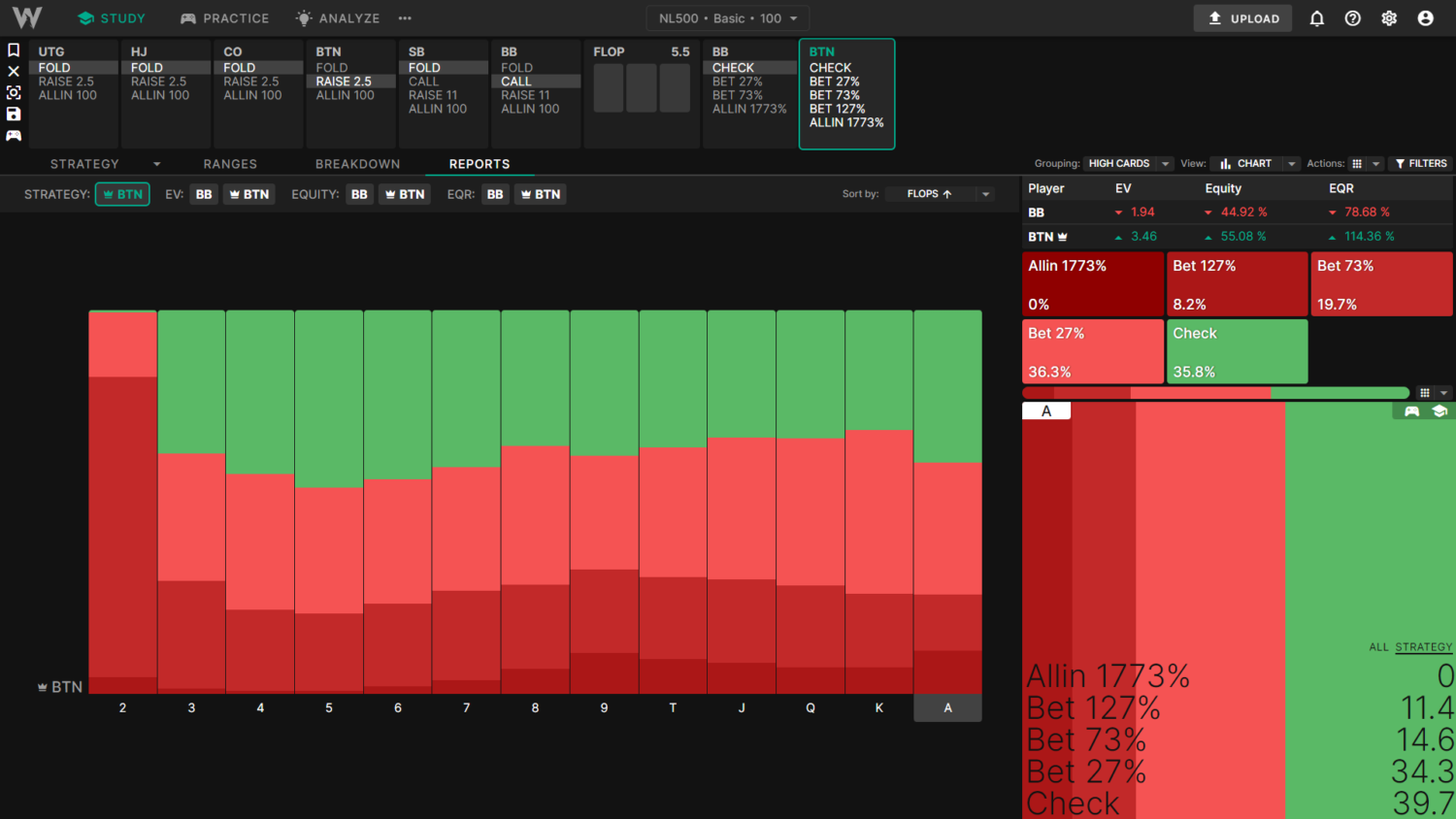
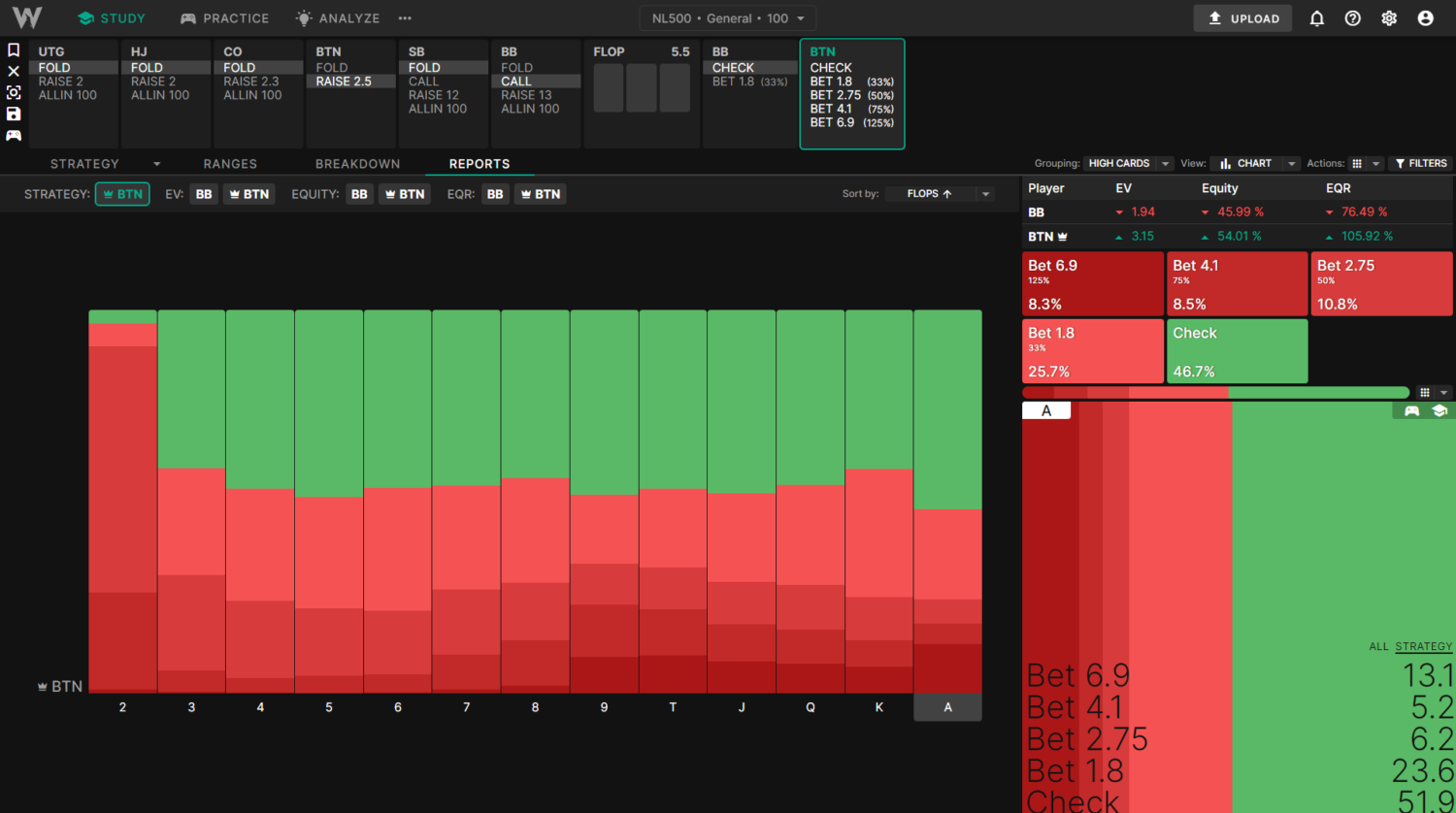
Example 3: BTN vs BB SRP aggregate reports with and without tiny bet sizes

This example compares the aggregate flop c-betting frequency between General and Basic solutions.

The General solutions use a minimum flop cbet size of 33%, which reduces the betting frequency. BB uses a larger, more polarized 3bet size, leading to a slightly stronger preflop calling range. Across all 1755 Strategically distinct flops, BTN cbets about 53% of the time.

The Basic solutions use a minimum of 27% flop cbet, leading to more frequent betting. BB also uses a smaller, more linear 3bet size preflop, leading to a slightly weaker calling range. Across all 1755 strategically distinct flops, BTN cbets more often, about 64% of the time in total.

Before we proceed, I feel I should address a well-known cognitive bias. Poker players are wired to think that betting more often automatically means higher EV or that the solution is somehow better. This simply isn’t the case.

For example, If you give the solver only a small bet on a flop like AK6r (BTN vs BB SRP), it will bet at a high frequency. If you then add an overbet in addition to the small bet, it will shift all of its value into the overbet line and check significantly more often. In other words, it will check more despite the new overbet strategy being higher EV.

Recreating GTO Wizard solutions

Now that you’re well-versed in the chaos theory of solvers, it’s time to try and recreate GTO Wizard sims.

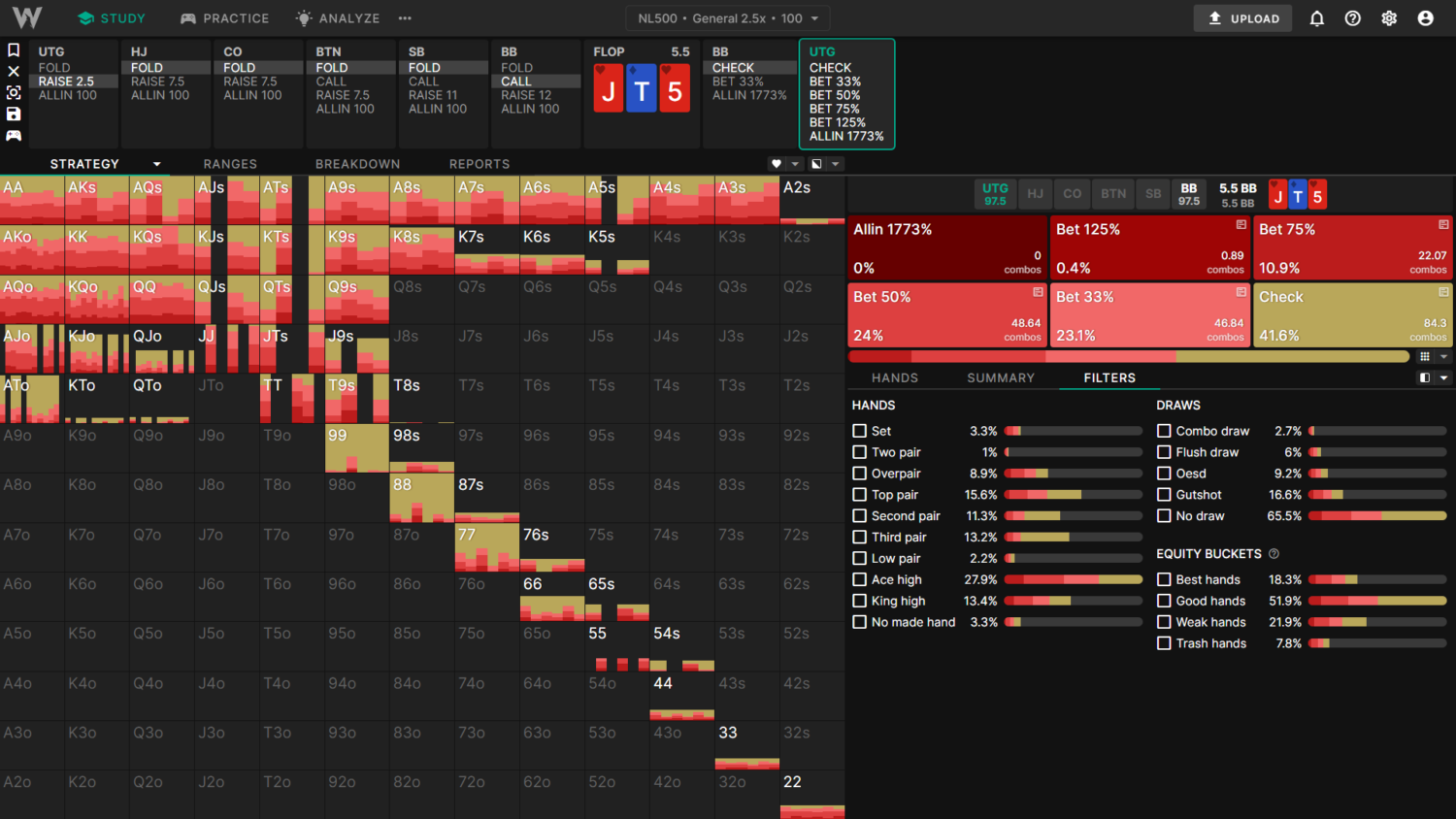
For this example, we’re looking at an UTG vs BB SRP on JT5. I’m using the 500NL General 2.5x solution (UTG opened 2.5BB). Follow these steps to recreate solutions using your own solver.

Setting up the tree

If you use Piosolver, you can simply copy and paste these parameters into your tree-builder. This isn’t an exact replica of GTO Wizard trees. For example, I’ve omitted the donk bet, which won’t get used on this board.

If you need a smaller tree, try omitting unused or strategically similar sizes. As a rule of thumb, river complexity has a smaller effect on the flop than turn complexity. Put another way, further away nodes have a smaller impact on your current decision.

Comparing results of different solvers

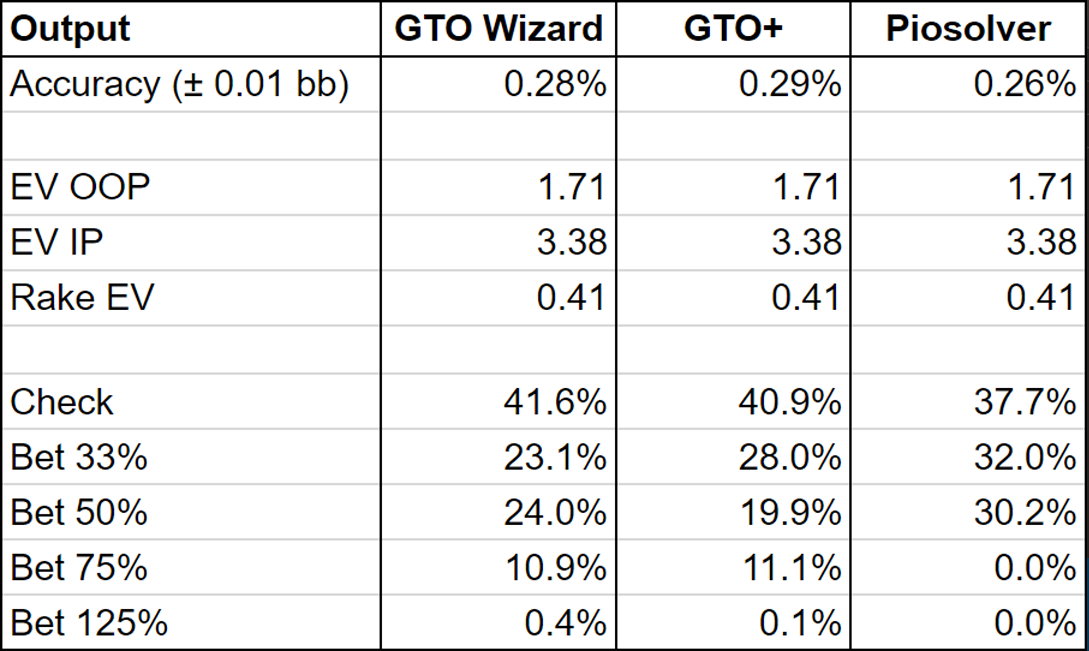
For this experiment, we’ll compare the GTO Wizard solutions to GTO+ and Piosolver outputs given the exact parameters above.

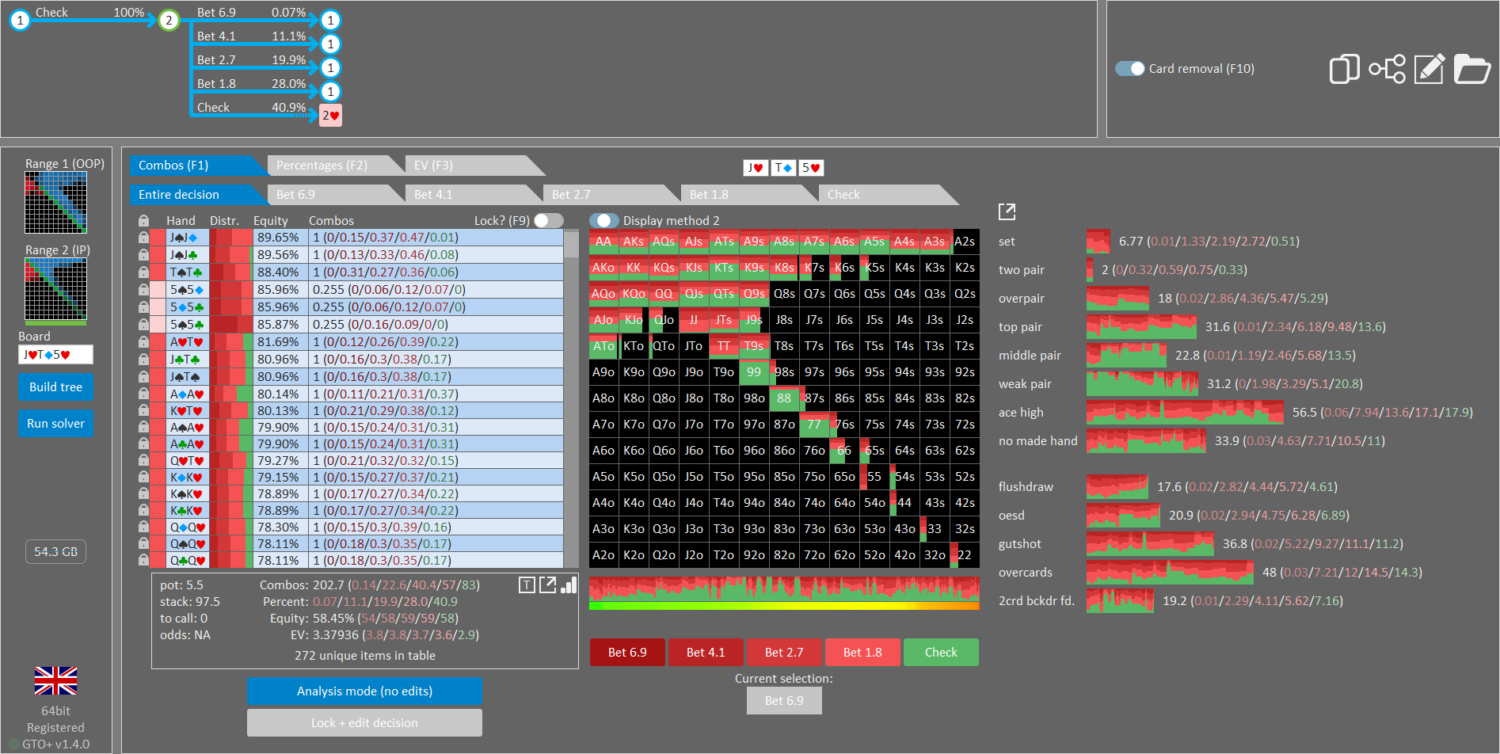
The GTO Wizard solution looks like this:

The GTO+ solution looks like this:

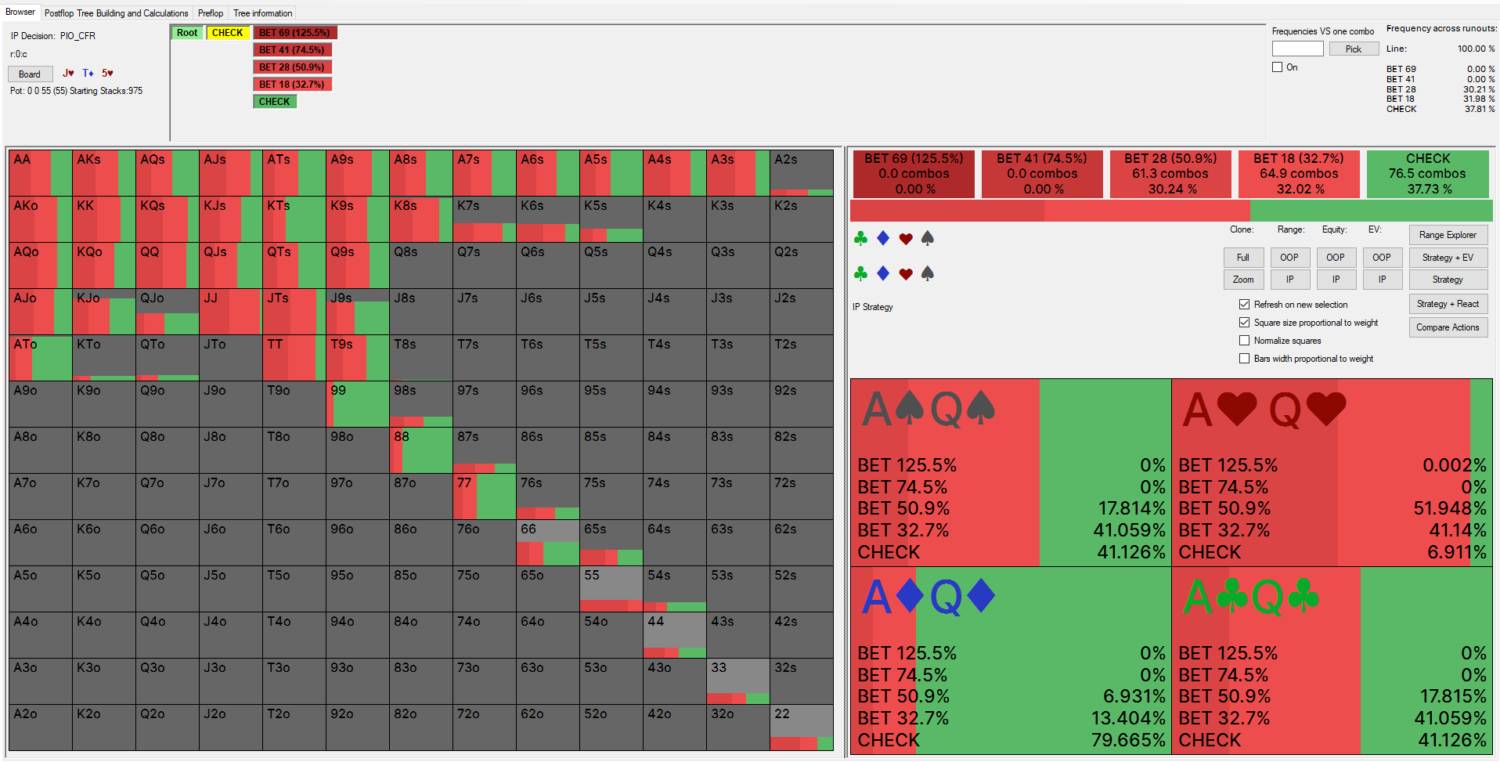
The Piosolver (CFR algorithm) solution looks like this:

Comparing results:

I’ve picked this board specifically because it’s a spot where many different strategies have similar expected value. All three of these strategies are playable. All three of these strategies can be exploited for, at most, 0.017BB (0.3% of the 5.5BB starting pot).

There is no one correct strategy, there are often multiple.

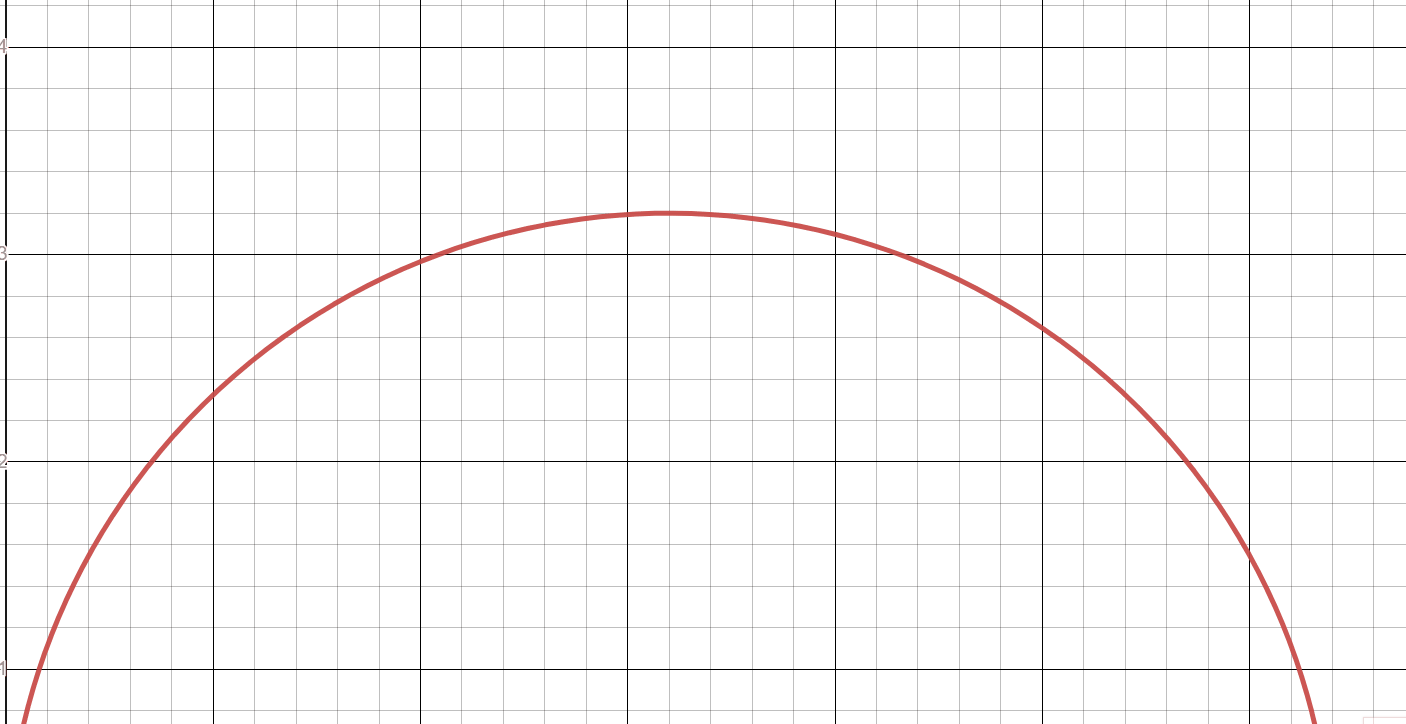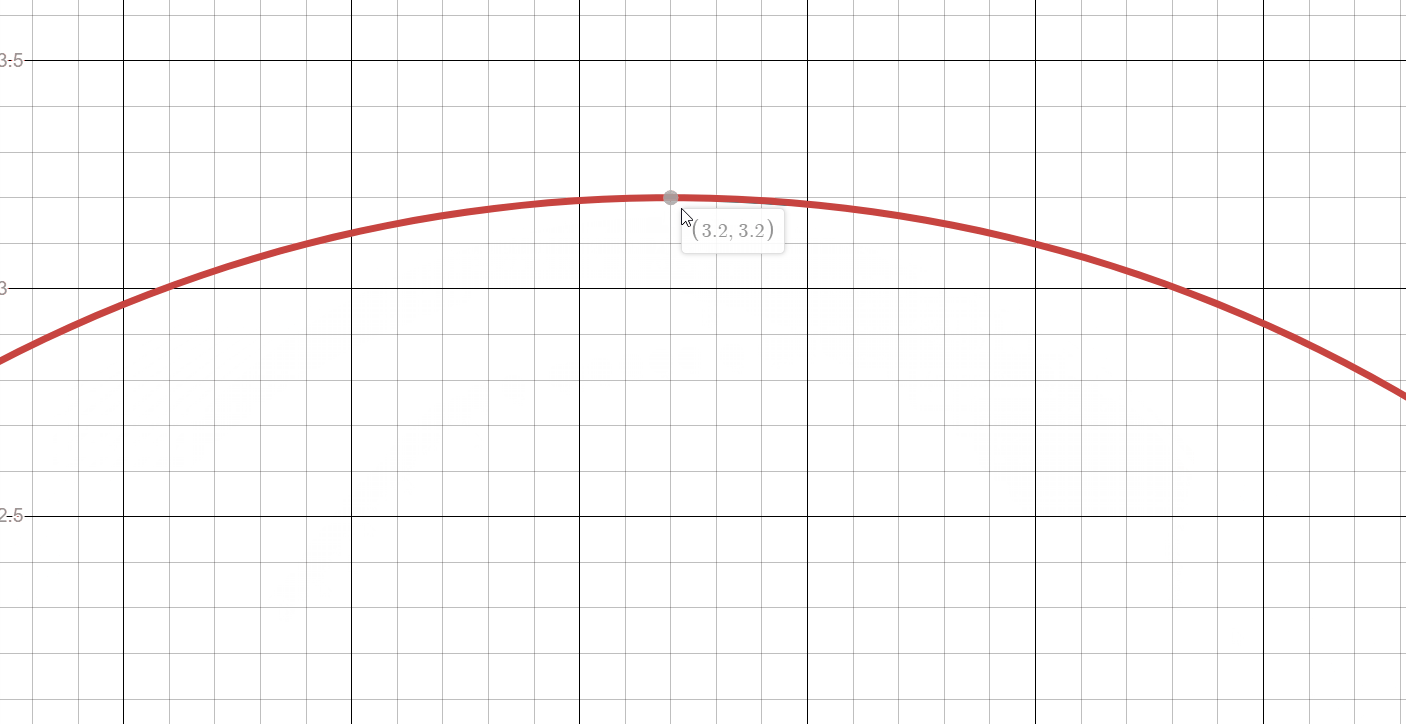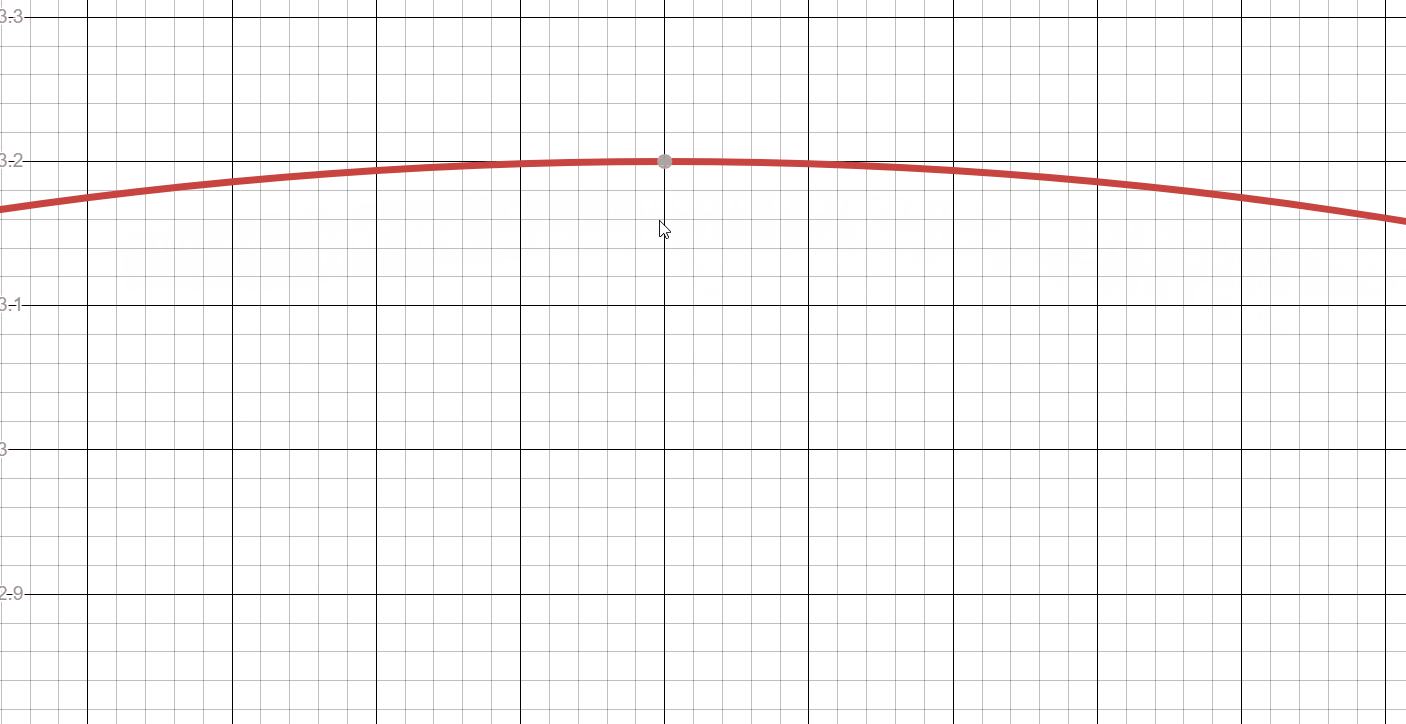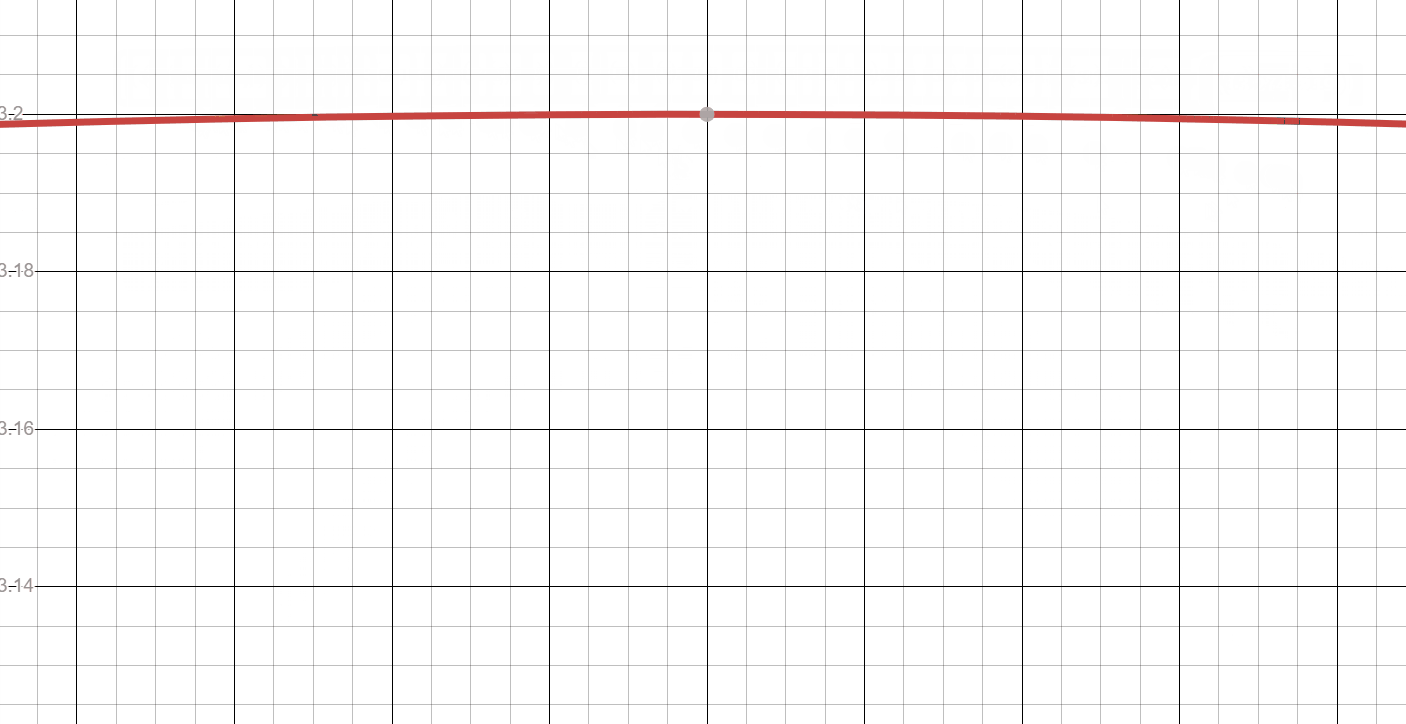
Let’s use an analogy to understand this concept. Picture a semi-circle. Each point on that circle represents a different strategy. Two dots right next to each other may represent completely different strategies with the same expectation. The height of each point represents how “good” (read: exploitable) the solution is. As you zoom in, it becomes harder and harder to distinguish which strategies are better.

If you wanted to force all three algorithms to produce the same strategy, you could try solving to ultra-high accuracy; way beyond what is considered standard practice or feasible for a massive solution library such as GTO Wizard. However, there is no guarantee that you’d get the same output since there may be multiple equilibria with the same expectation.

To put things simply, the GTO solution, in practice, isn’t always one well-defined strategy. There can be multiple correct ways to play.

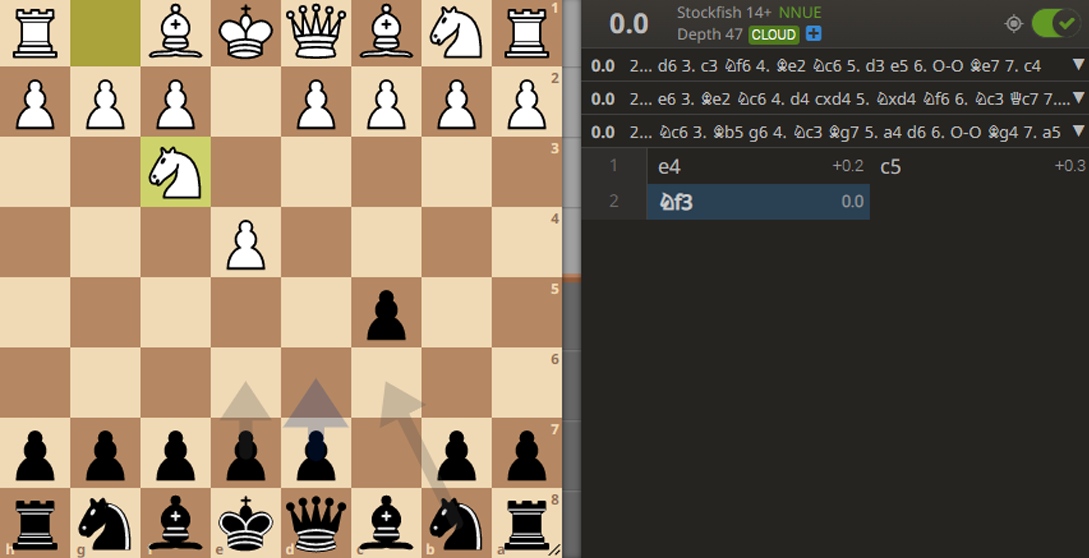
This concept exists in almost all strategy games. For example, here’s a chess position, solved to ultra-high accuracy (47-ply). The solver calculates that all three moves, d6, e6, and Nf6, have the same expectation of 0.0. Of course, all three of these moves have different ideas and strategies. But they’re all playable, even at the highest levels:

So what to take away from this?

Some spots have many equivalent strategies. The exact solution you’re working with isn’t that important, so long as the input parameters correctly model the situation you’re studying.

Instead of fixating on the exact strategy for some node, focus on these three things:

Conclusion

It’s normal to feel slightly discouraged when first learning about the chaotic nature of GTO solver outputs. It feels like yet another layer of complexity in an already difficult endeavor. But your goal should not be to memorize solutions; instead, your goal is to understand the underlying reasoning behind these strategies.

Rote memorization is not only impossible, but it’s also incredibly ineffective. If you instead focus on the underlying principles, you will have a much better idea of how to construct your range in various spots. Furthermore, studying principles is required to make exploitative adjustments.

GTO Wizard offers dozens of solutions for different rake structures, bet sizes, and stack depths. Use this to your advantage. Compare similar solutions and figure out why the strategy changes! Ask yourself how the solutions differ and how those changes interact to create different strategies. Strive to understand WHY rather than WHAT. Comparing and contrasting solutions will ultimately give you a much deeper understanding of GTO in the long run.