Overchoice: Making Sense of Multiple Sizings
Solver solutions with multiple bet sizes often involve a lot of mixingMixed strategy
To mix between different actions with the same hand. For example, if AK always bets 1/3 pot on K♦9♥6♠ in a BTN vs BB SRP scenario, this would be considered a pure action. If that same hand sometimes bets 1/3, sometimes bets 2/3 and sometimes checks, that would be a mixed strategy.. See indifference. between those sizes, thereby blurring the heuristics underlying sizing decisions. If any hand can bet either size, then what’s the point of using multiple sizes? How would you ever choose, in a real game situation, which to use with a given hand?
This is where solvers come in handy, not to memorize outputs but to learn from them. Your goal, when studying with GTO Wizard, should be to understand why solutions look the way they do. Understanding the underlying drivers will enable you to apply them to many situations, not just the one you are currently examining.
The nodelocking feature offers a powerful new tool for studying complex solutions. It enables us to test the function of each strategic option (bet, check, raise, etc.) in a strategy by eliminating that option or by locking the opponent’s response to see how our incentives change. In this article, we’ll do a deep dive into a common flop decision—whether to bet small or large—to demonstrate how nodelocking can aid your study.
Search for Pure Strategies
You can build intuition around what motivates the use of a particular bet size (or other strategic option; the same logic applies to checking, calling, raising, and even folding) by searching for hands that purelyPure strategy
A strategy in which the same action is always taken at the same decision point without mixing. For example, AA is a pure raise in the BB facing a BTN open in a 100bb cash game. take that action. These are the hands that are not indifferent, where you have a clear incentive to prefer one option over another. In the absence of any pure strategies, look for the hands that take that action at the highest frequency.
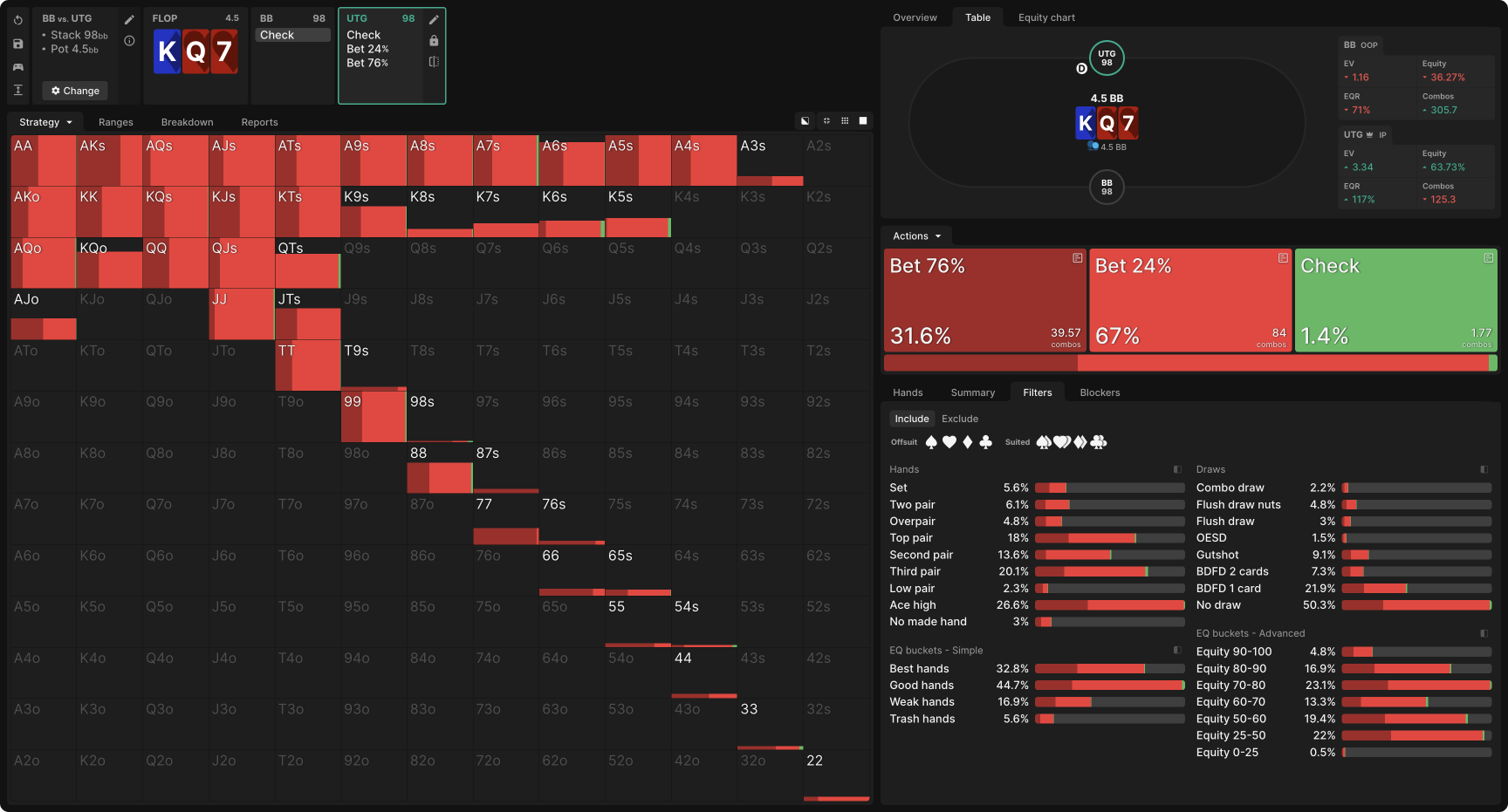
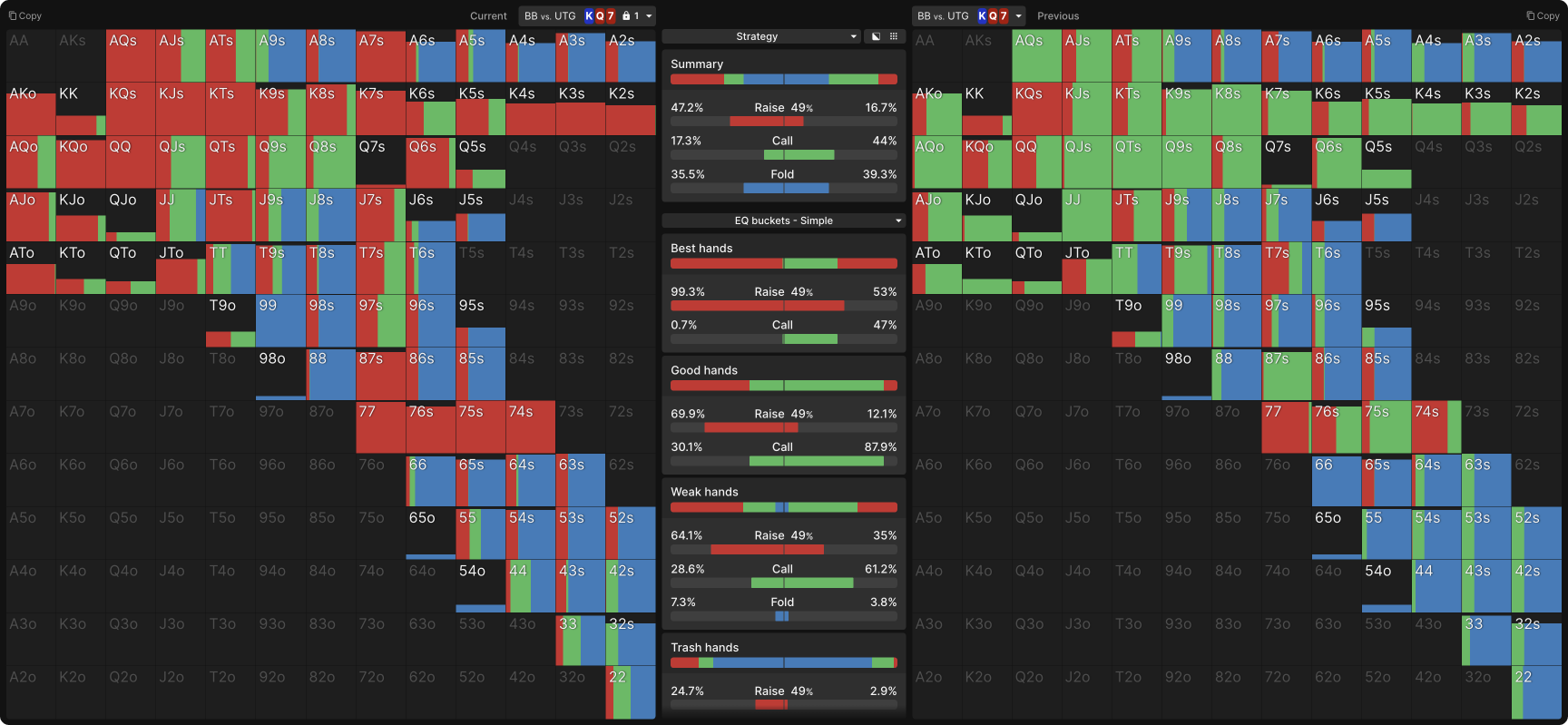
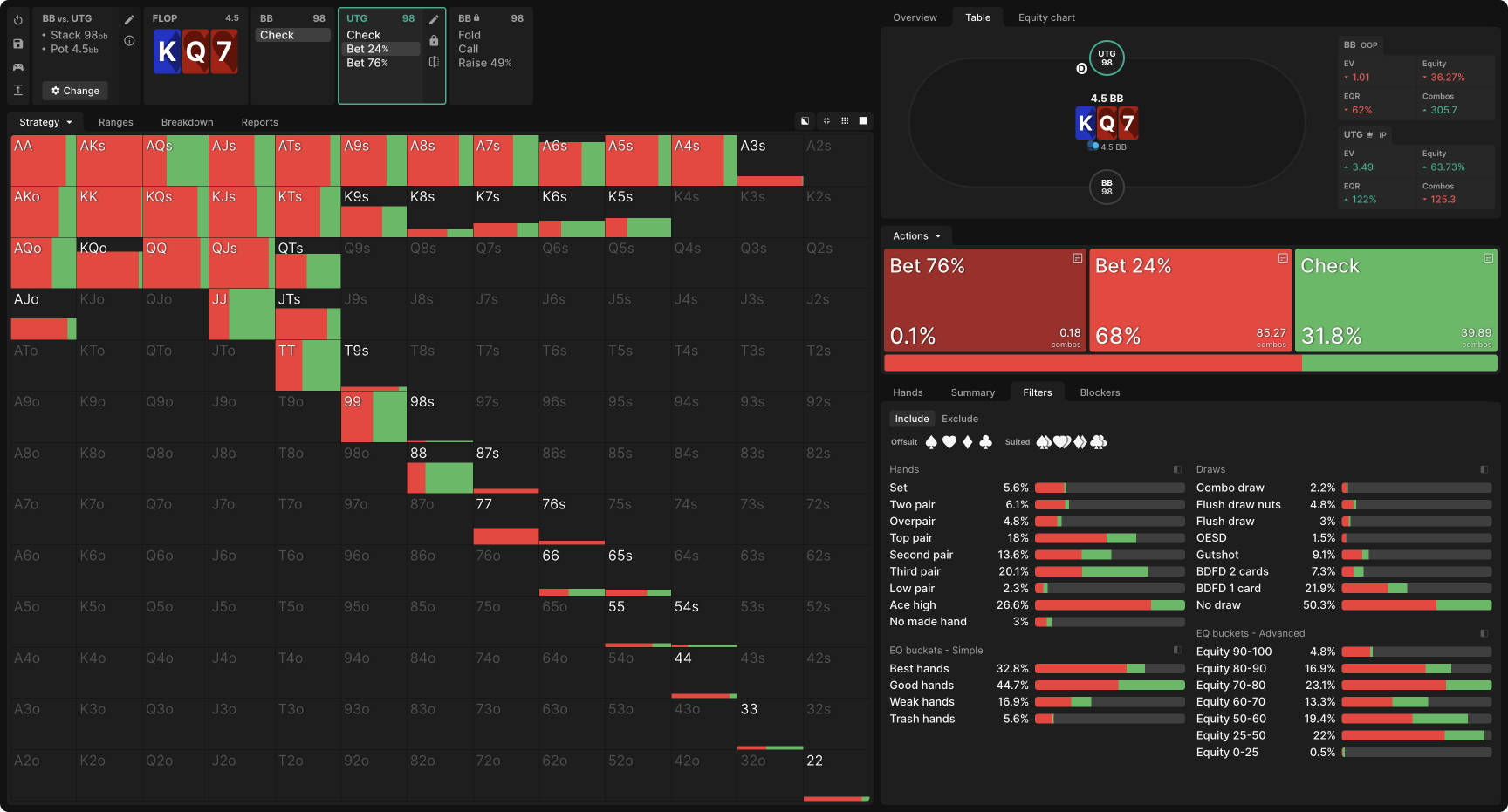
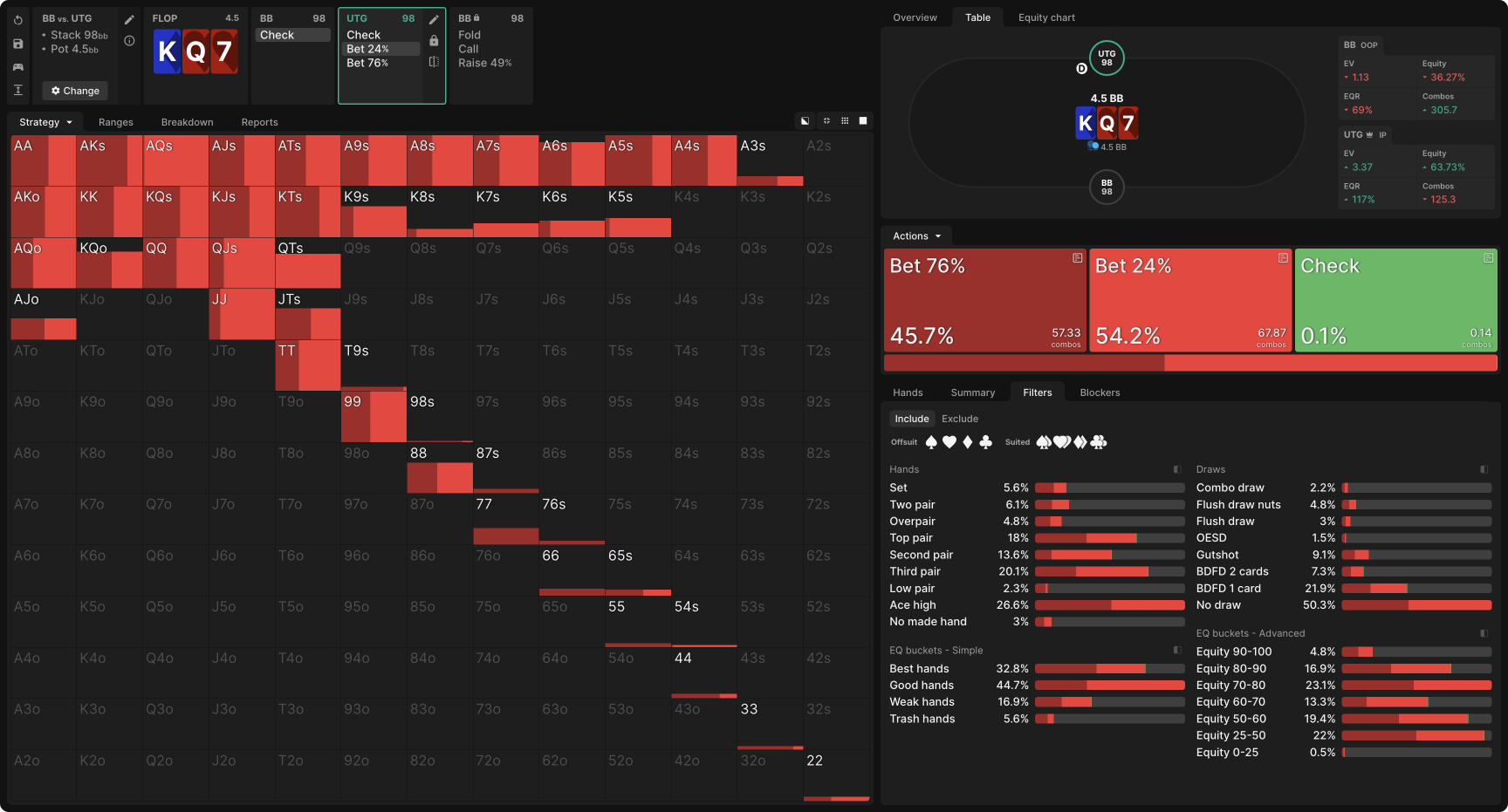
Consider this example from a 9-handed cash game with 100bb stacks. UTG open-raises to 2bb before the flop, BB calls, and they see a K♦Q♥7♥ flop. After BB checks, UTG may check or bet either 76% or 24% of the pot. As you can see, the solver never checks (that 1% is a convergence error—if the simulation were to be run to 0 exploitability, it would disappear), but it makes substantial use of both bet sizes, with most hands appearing to mix between them:
If you wanted to play a simple strategy on the flop—not a bad idea if you’re new to this GTO stuff—then you can conclude from this result that betting small with your entire range would be an acceptable strategy. But those bigger bets are there for a reason. Determining that reason will lead you to an EV increase compared to the simplified strategy of range-betting for a small size.
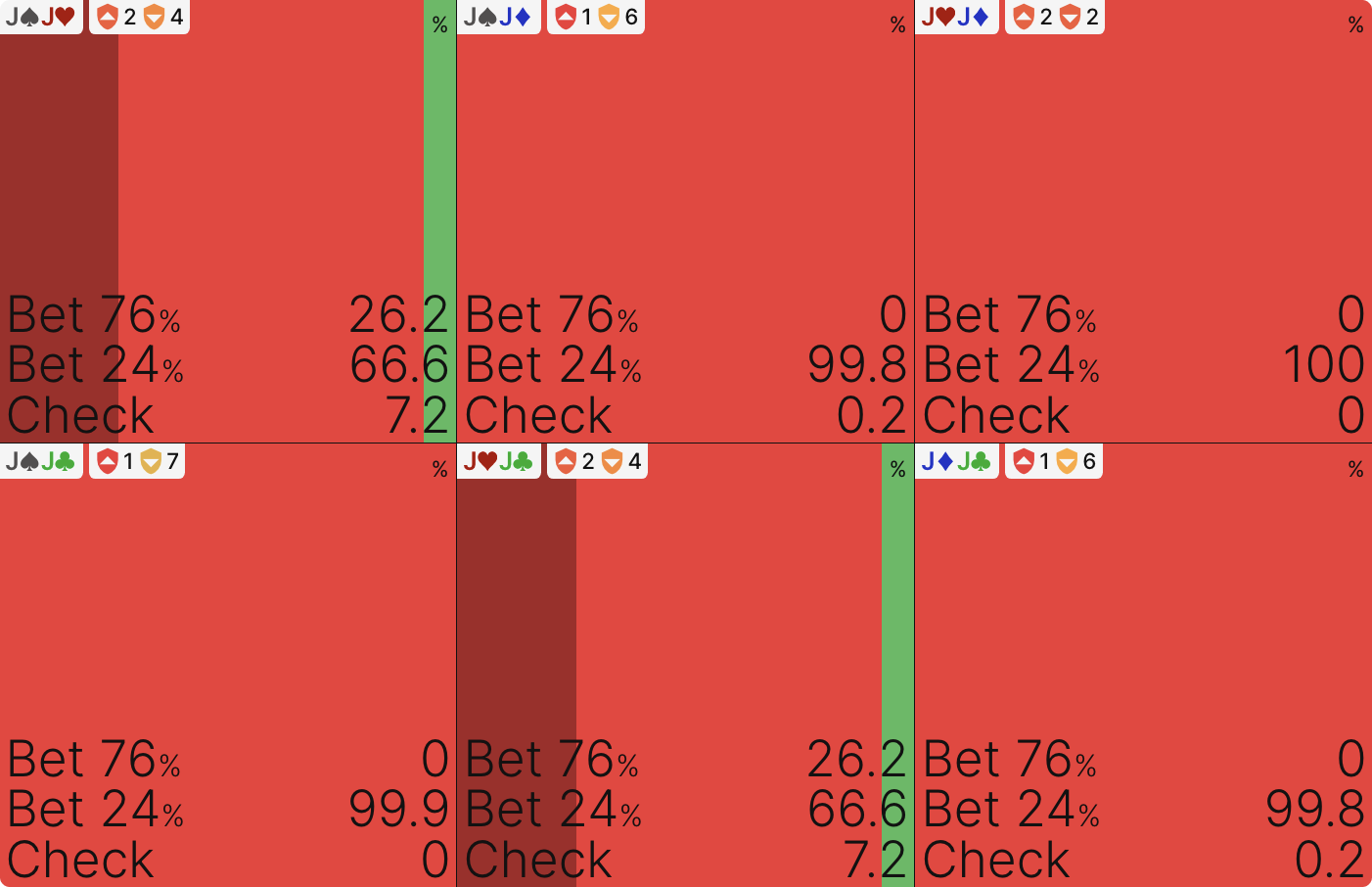
Start by looking for the exceptions, the hands that purely bet one size or the other. The immediately apparent ones are AQs, K8s, K7s, and K6s. If we dig deeper, we see that some of the other mixes are suit-dependent. For example, the medium pocket pairs with a heart tend to mix, but without a heart, they tend to purely bet small:
Some traces of this behavior can be found for hands like K5s as well for example:
What do these hands have in common? They are all medium-strength, reasonably strong hands ahead of much of BB’s range but in bad shape against top pair or better. That suggests the reason why they prefer the smaller size: they benefit from denying equity and getting called by BB’s weaker hands (the ones that might fold to a larger bet). However, if they put too much money into the pot, they will concentrate BB’s range around the strongest hands against which they perform poorly. Thus, they avoid the larger bet size and bet 24% pot exclusively.
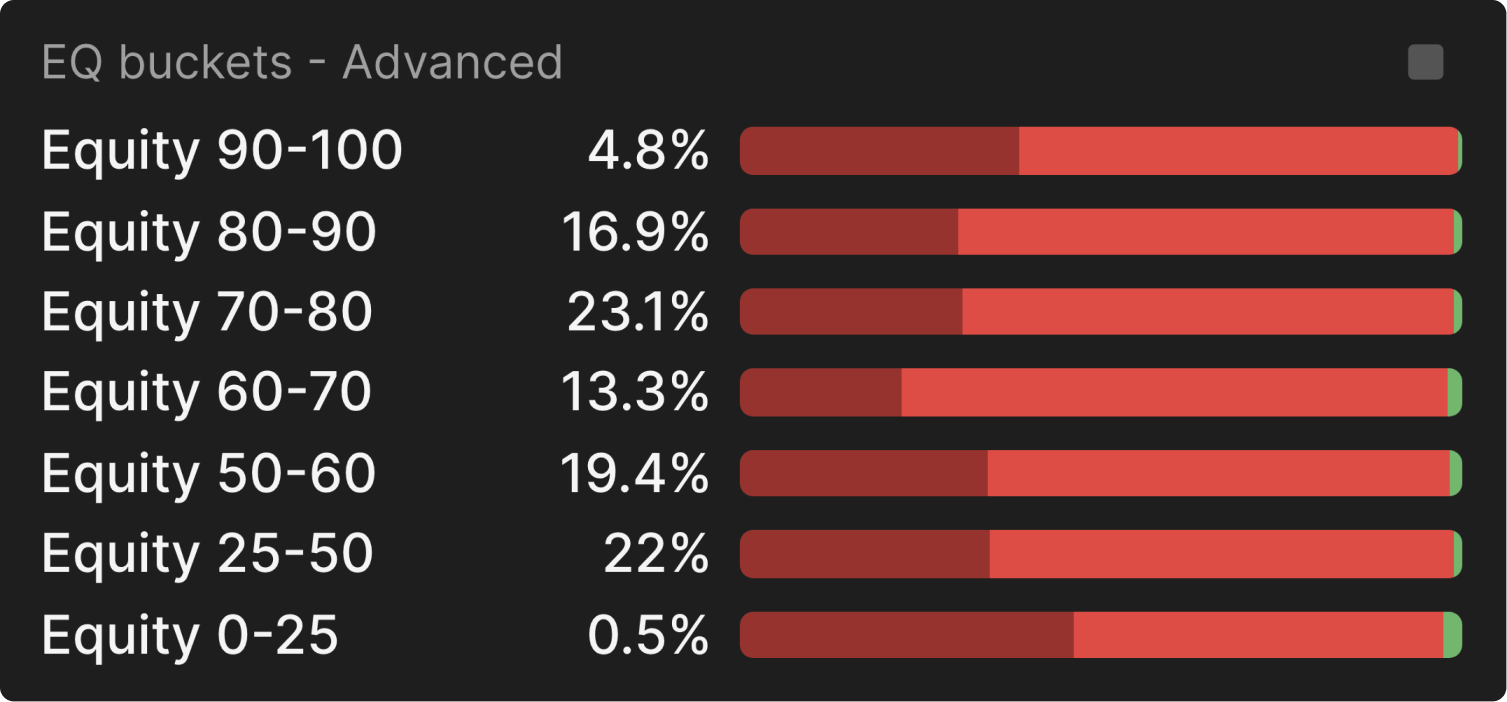
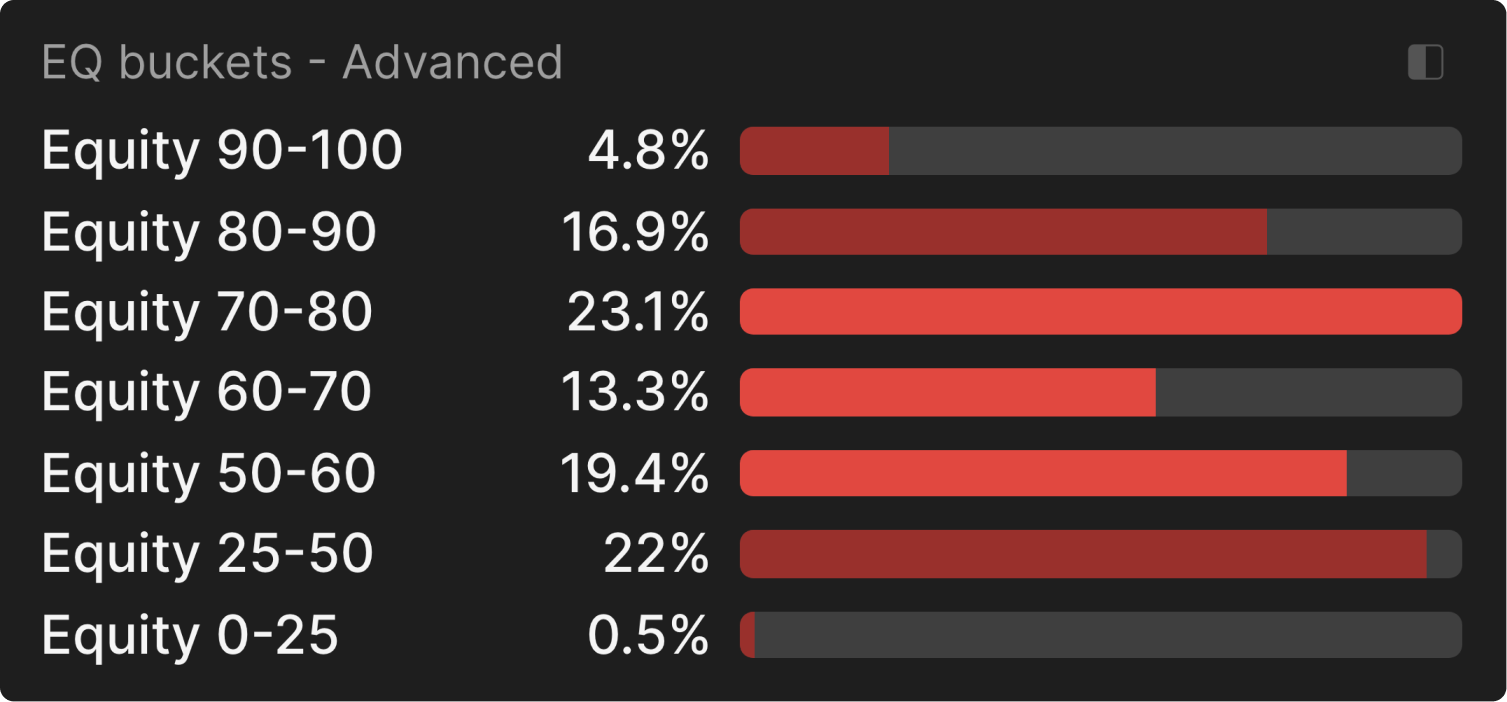
We can confirm this by looking at the equity buckets, where we can see that UTG uses the big size most often with their strongest and weakest hands, and the small size mostly with their middling hands:
The bigger you bet, the more you concentrate your opponent’s range around their strongest hands.
This explains why the small size is used. UTG wants to bet their medium hands, but they can’t do so profitably for a large size. We can prove that with a custom solution only allowing the 76% pot bet. In this scenario, UTG cannot profitably bet their entire range, and it is these same medium-strength hands that fill out the checking range:
Explain the Anomalies
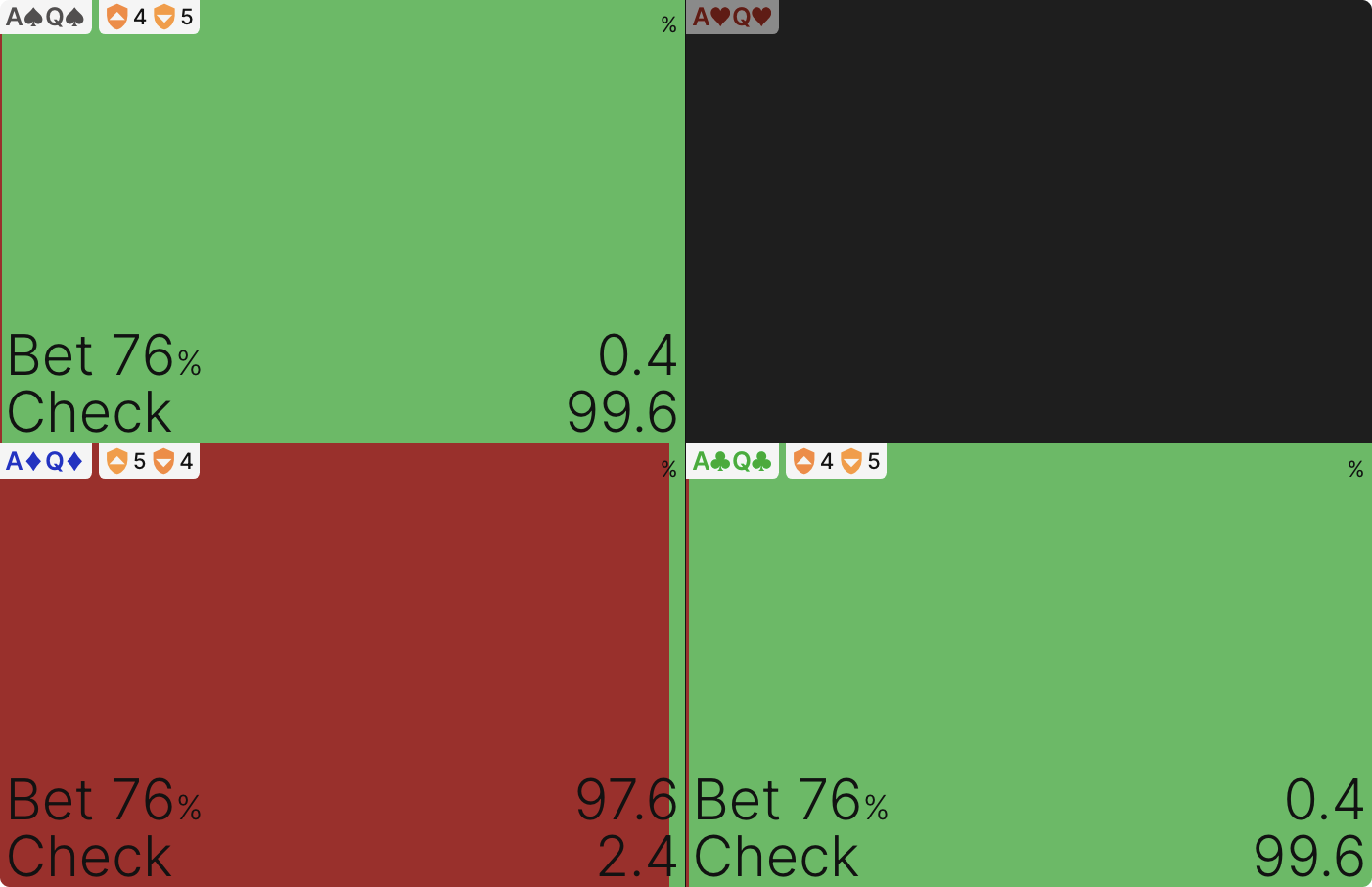
The primary purpose of the small continuation bet appears to be to accommodate the many medium-strength hands in UTG’s range. This is not a complete explanation, however, because it does not account for the presence of strong hands like AA and K7s in the small betting range. Why don’t these hands strictly prefer the larger bet, given that they actively benefit from growing the pot against the top of BB’s range?
The common explanation is that these ‘monster’ hands “protect” the medium hands by discouraging BB from raising, but that’s a bit misleading. It implies the strongest hands are making a sacrifice by foregoing a higher EV option for the sake of other hands in your range.
This kind of sacrifice is never a feature of GTO solutions. Solvers do not give up EV with one hand to increase the EV of another. If a hand mixes between multiple bet sizes, then, at equilibrium, it has the same EV with all of them.
Solvers never sacrifice EV with one hand to increase the EV of another.
That raises a new question: where does the EV in the small bet line come from for the stronger holdings like AA and K7s? How does betting small win just as much as betting large?
A good way to approach such questions is to investigate the counterfactual. What would happen if UTG never bet small with their strongest hands? We can test this with a custom solution where UTG is nodelocked to strictly bet big with their strongest and weakest hands, and small with their medium hands.
A node comparison reveals that BB folds about as often to a small bet from this range as they did to the small bet in the unlocked sim. The major difference is that they raise three times as often!
You can intuit how an equilibrium works by thinking in terms of balancing a scale. For UTG, the EV of betting small with strong hands depends on BB’s check-raise frequency. And for BB, the EV of check-raising depends on UTG’s small betting frequency with strong hands.
BB’s incentive to raise a small bet comes from UTG’s medium hands. Their incentive to call comes from UTG’s strong hands. When UTG gets the ratio of big to medium hands in their small betting range exactly right, BB is indifferent between raising and calling with hands like ATo and 76s.
Likewise, when BB gets their raising frequencies exactly right, then UTG is indifferent between betting big and betting small with their strongest hands. The strong hands aren’t sacrificing anything. They are betting small for their own sake because they expect to profit exactly as much from that bet as they would from the larger bet.
We see this effect if we nodelock BB to check-raise twice as often against a small bet as they would at equilibrium. UTG stopped using the large bet size entirely because even their best hands now make more money from betting small:
UTG also prefers to check many of their weaker hands against this hyper-aggressive raiser, which gives rise to a new set of incentives. If the checking range is weak, BB has a lot of incentive to attack it with big bets on the turn. Indeed, when only a single bet size is allowed, GTO Wizard chooses to overbet nearly 3x pot with 21% of hands on a 2♠ turn:
If they get that overbetting frequency exactly right, then UTG also has some incentive to check their strongest hands to induce these overbets. Just like with the balancing between UTG’s small “trap” bets and BB’s raises, a new equilibrium emerges between UTG’s trap checks and BB’s overbets.
Make Exploitative Judgment Calls
What does all this mean for you, in practical terms? How does it help answer our original question about how to choose a bet size over the felt?
Once you understand which of your opponent’s actions incentivize you to take each line, you can consider which imbalances are more likely in this situation. With some hands, you have a purely preferred option that does not depend a lot on your opponent’s response. If you can recognize those hands, you can play them accordingly.
When you believe your hand is mixing options because it’s indifferent at equilibrium, then the EV of both options will be close against a well-balanced opponent, so it won’t matter which you choose. This frees you up to act on hunches, as even if you are wrong and play a pure strategy to exploit a mistake your opponent isn’t making, you won’t pay the penalty for it (unless they are actively unbalanced in the opposite direction from what you assumed).
Once you understand which of your opponent’s actions incentivize you to take each line, you can consider which imbalances are more likely.
Against an overly aggressive opponent, you’d purely bet small with your strong hands to induce raises, as we saw in our example above. Against an overly passive opponent, you’d purely bet large with the same hands because you wouldn’t expect to make the money you’re “supposed” to make from inducing raises with the small bet.
Your opponent’s imbalances do not need to be as dramatic as the ones in our examples. We deliberately looked at extreme examples to make the point more clearly.
Here is UTG’s continuation betting strategy if we nodelock BB to check-raise half as often against both bet sizes (and never to donk bet, which the solver would otherwise do to compensate for the reduced check-raising but which a passive opponent presumably would not):
Strong hands still mix between both sizes, but the big bet size is preferred much more often in general. The same hands retain their preference for the small bet, however, such as JJ, K6, and AQ without a heart.
Conclusion
Pure strategies are indicative of hands that have strong incentives to take a particular line. Understanding those incentives helps you see why that line is strategically important.
Deception is also important, however, so it’s rare that you can get away with only taking that line with the “obvious” hands. Your opponent could deduce what you’re trying to accomplish and adapt their own play to frustrate your efforts.
Nodelocking enables us to simulate this process. We can lock the Hero to play a less deceptive strategy and see what that incentivizes the opponent to do in response. Those responses are what motivate Hero’s own mixed strategies, creating a balance between the opponent’s potential exploits and Hero’s “traps”.
With all those heuristics sorted out, we can come away with practical considerations to guide in-game decision-making. In this example, we determined that medium-strength hands strongly prefer small bets, while stronger hands are torn between betting bigger to win more from calls or smaller to win more from raises.
Both sizes are equally profitable at equilibrium, but your opponents will not play perfectly balanced strategies. Guided by the heuristics you learned, you can make judgment calls about which size will be better in a specific situation.
Author
Andrew Brokos
Andrew Brokos has been a professional poker player, coach, and author for over 15 years. He co-hosts the Thinking Poker Podcast and is the author of the Play Optimal Poker books, among others.