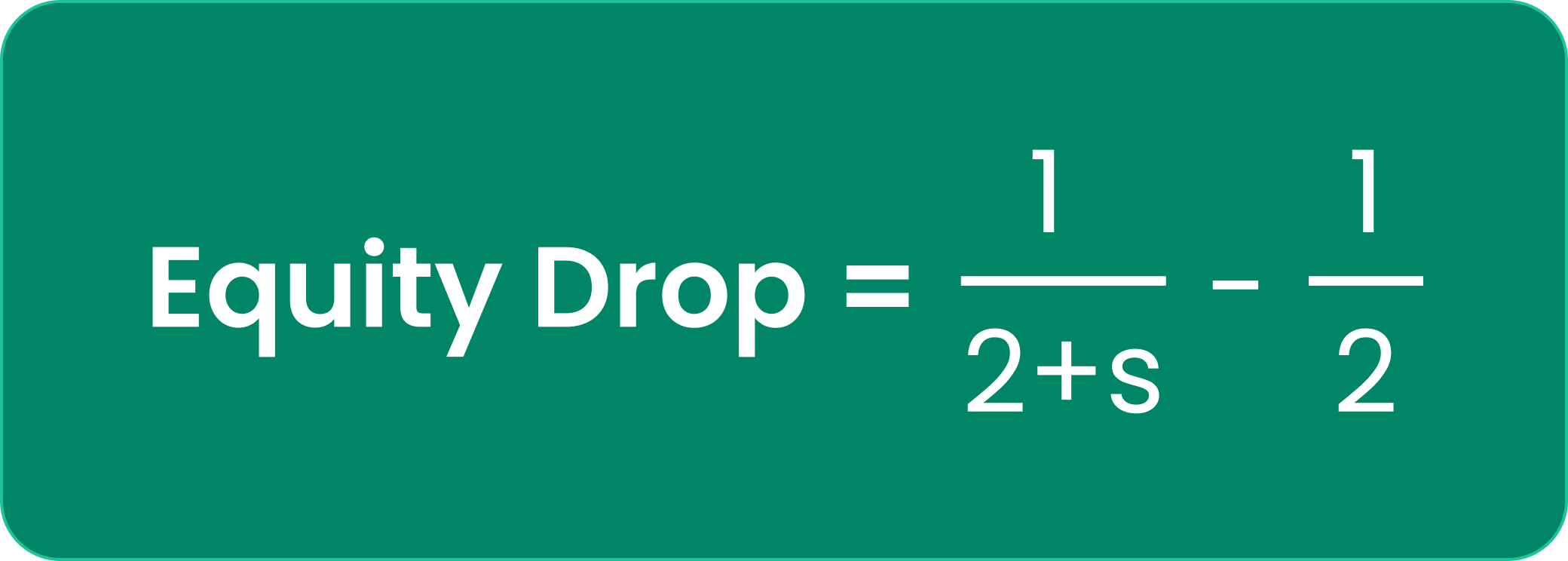The Theory of Bounty Tournaments – Part 3: Key CalculationsCalculating the Value of a Bounty and ICM Risk Premium Reductions with Entry Fee Data

Parts 1 and 2 in this bounty theory series describe how total risk premiums are lower across the board in bounty tournaments than in non-bounty tournaments. They also discuss how a number of factors impact the in-game value of a bounty, with the primary factor being how much of the entry fee goes into the bounty prize pool as a percentage of the total buy-in (minus rake). The higher the percentage of the entry fee assigned to the bounty prize pool, the more bounties impact our strategies in every hand.

This article explores how:

The value of a bounty—expressed in either chips or equity drops—directly correlates to the ratio of the bounty share of the entry fee to the total entry fee.
The difference in the ICM risk premiums between a regular MTT and the regular prize pool of a similar bounty MTT also directly correlates to the buy-in ratio.

Calculating Bounty Value
by the Proportion of Bounty Entry Fees

The absolute value of a bounty—its real-world dollar value, for example, $10 or $10,000—has no impact on our strategy in theory. What does impact strategies, however, is the degree to which the bounty influences bubble factors (total risk premiums), which correlates to the ratio of the bounty prize pool to the total prize pool. This is most easily demonstrated by calculating the value of a bounty in chips and/or its equity dropEquity Drop
Needs updating (Glenn sorting out with the author) at the start of the tournament.

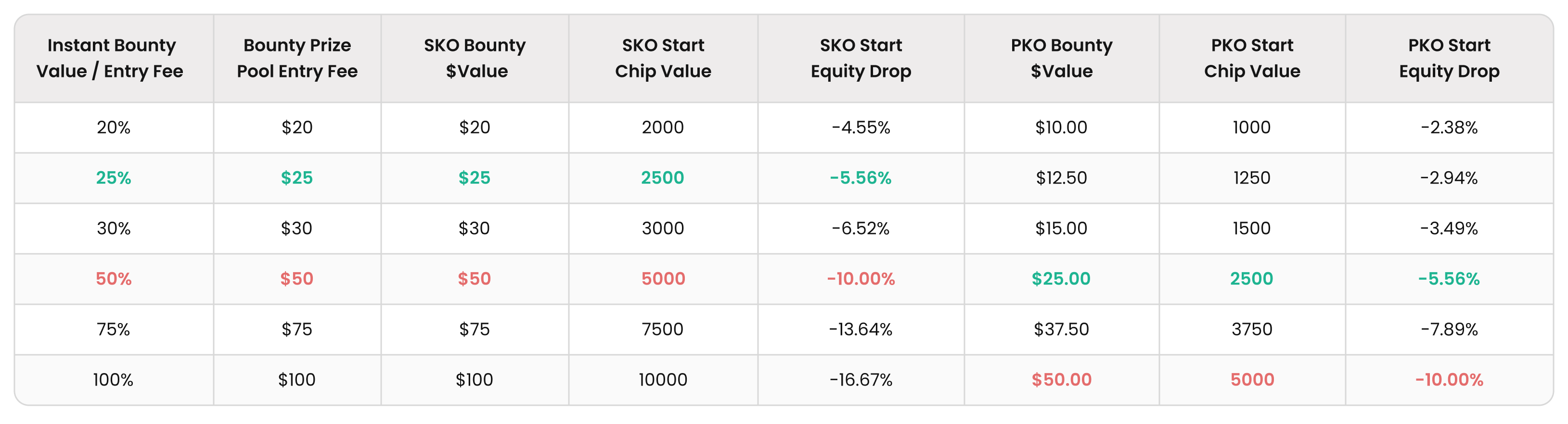
Whether the bounty format is a Standard Knockout (SKO) or a Progressive Knockout (PKO), at the start of the tournament, the metaphorical chip or equity drop value of the bounty can be calculated by dividing the $value of the instant bounty that can be won upon eliminating a player by the total entry fee (minus rake). In an SKO, the bounty $value will be the same as the portion of the entry fee that goes to the bounty prize pool. In a PKO, half of the portion of the entry fee will go toward the bounty prize pool, with half of that amount (or ¼ of the entry fee) being the instantly unlockable bounty since the other half of the eliminated player’s bounty is added to the winning player’s bounty.

Below are some examples of how the following values correlate for SKOs and PKOs:

Bounty $values
Bounty start chip values
Start equity drops

(The data assumes bounty MTTs with a $100 total entry fee (after rake), a starting stack of 10,000 chips, and a 50% instant bounty in the PKOs.)

In general, the relationship between starting stack% and equity drops can be summarized as follows:

Where:

Explanation: Here’s how to derive this equation. Villain shoves on the first hand of a tournament, without a bounty, your pot odds approach ½. With a bounty, we can add the bounty (as a starting stack ‘s’) to the reward side of a pot-odds calculation, so your required equity to call becomes 1/(2+s). The difference between your pot odds with and without this bounty represents your equity drop (risk premium ignoring ICM).

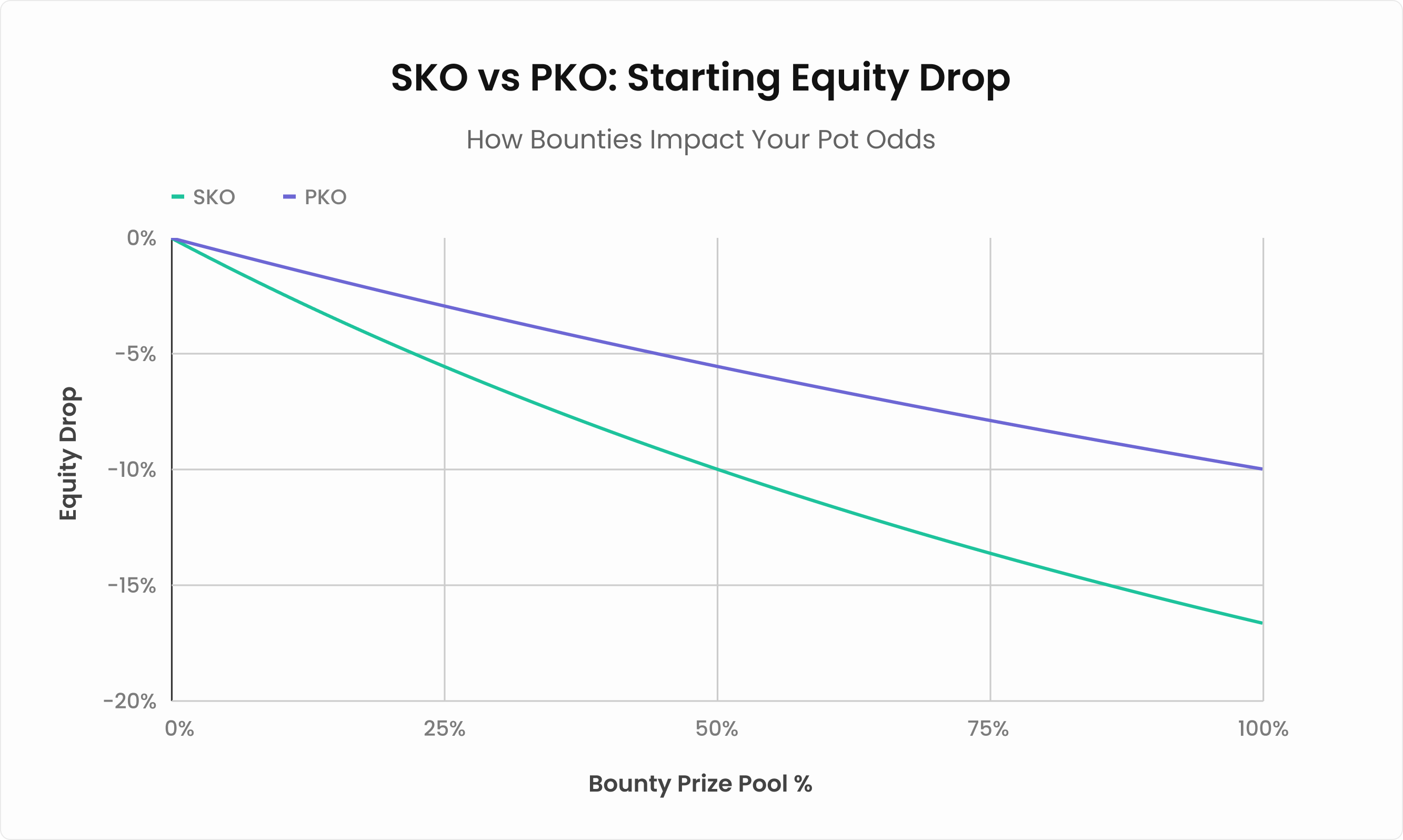
Let’s graph the equity drop comparison between SKOs and PKOs to demonstrate the differences in equity drops between them with various amounts of the entry fee added to the bounty prize pool:

As the chart above shows, the start equity drop and bounty value in chips for a 50% PKO is the same as it is in a 25% SKO. The bounty value in chips and equity drops are identical because, in the SKO, the covering player immediately wins the full bounty amount, whereas in a PKO, the winner only receives half of the 50% bounty. Half of the 50% bounty equals to 25% of the total buy-in to the tournament, which is the same as in a 25% SKO.

Similarly, the values for a 50% SKO and a 100% (total) PKO are the same, as the instant bounty won when eliminating another player in the 100% PKO is the same $value as the bounty in the 50% SKO.

Note that the maximum value for a bounty, at the start of a tournament, is one starting stack or -16.67% (equity drop).

The correlation between the ratio of the bounty won and the total entry fee offers a useful guidepost for strategic adjustments, as a comparison of recommended solver strategies between an SKO and a PKO with the same instant $bounty shows that the adjustments are usually similar, and correlate with bubble factors (as well as their corresponding total risk premiums). In other words, the strategic adjustments that correspond with the same negative risk premium of a bounty in one type of bounty format will likely be similar to that of other bounty types (assuming everything else between the formats is the same).

In the end, our risk premium vs. the opponent, as well as the opponent’s actual range, are the two biggest influencing factors for the construction of our ranges and adjusting them.

Calculating the Reduction of Bounty ICM Risk Premiums
by the Proportion of Bounty Entry Fees

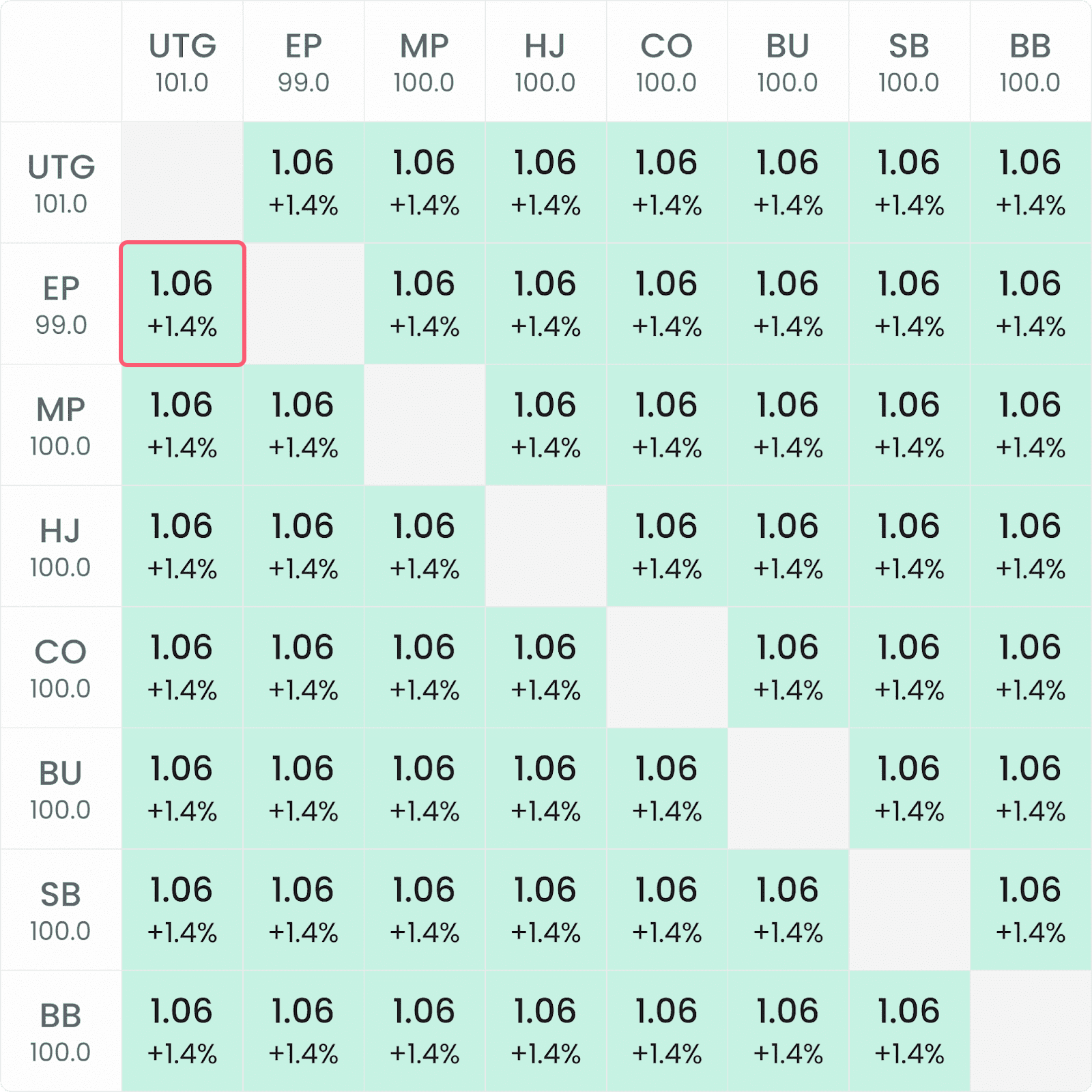
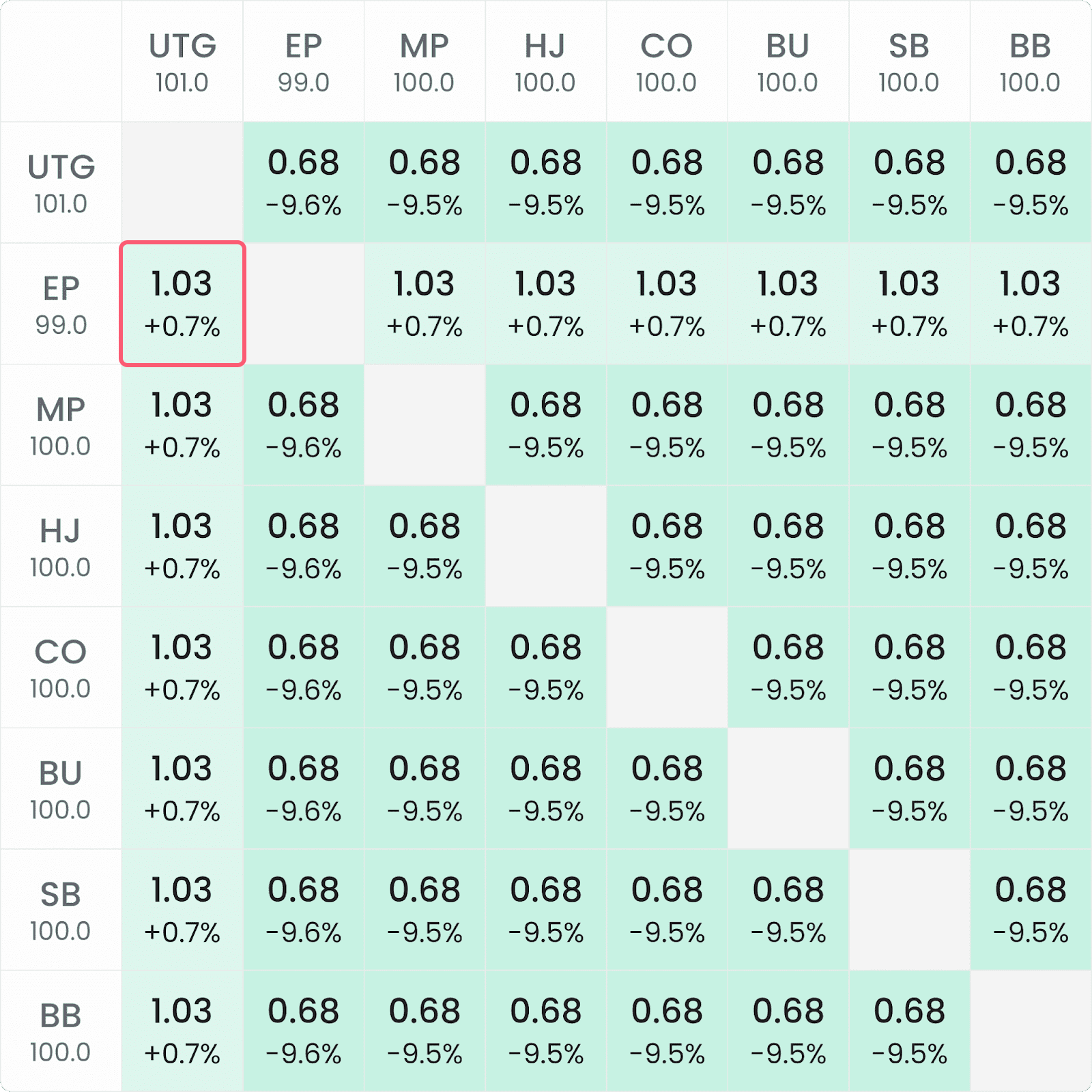
The previous article in this series compared the total risk premiums at the start of two different tournament formats, both with 1000 entrants: a classic non-bounty $100 MTT (left) and a $100+$100 Standard Knockout (SKO) tournament (right).

BFs & RPs (%)

2nd hand classic 1000-runner MTT → 2nd hand 50% SKO, 1000/1000 runners remain

In the classic MTT, all the players begin the tournament with a 1.06 bubble factor, which converts to a +1.4% risk premium. There is no significant difference between the risk premiums of the 99bb stack and the other players with 100–101bb.

In the SKO, on the other hand, the covered player (EP) with the 99bb stack experiences a significantly higher risk premium than the other players. As the EP player cannot bust any other players at the table in this hand, they do not experience an equity drop that comes from the potential to win a bounty. At the same time, however, the EP player has a lower total risk premium in the SKO tournament compared to the classic MTT: +0.7% < +1.4%. That’s a 50% decrease, which appears to correlate with the fact that 50% of the entry fee for the SKO is directed to the bounty prize pool.

As discussed in the first article in this series, the bounty prize pool is Chip EV and so isn’t subject to ICM as is typical of the entire prize pool in a regular MTT. If only half the prize pool in the SKO is impacted by ICM—with the other half unaffected—then theoretically, the total risk premium for the covered stack in the SKO should be around 50% less than the risk premium in the regular tournament.

The calculations above reveal that the EP vs UTG risk premium in the 50% SKO is 0.6859%, which amounts to 49.32%0.6859% / 1.3906% = 49.32% of the ~1.4% risk premium in the regular MTT. This is a reduction of slightly more than 50% (50.68%). As the EP’s share of the bounty prize pool after doubling increases more than their share of the ICM regular prize pool, the 50% SKO ICM risk premium is slightly less than half of that in the regular MTT.

Hypothesis: The proportion of the entry fee that goes to the bounty prize pool corresponds with the reduction in total risk premium pressure.

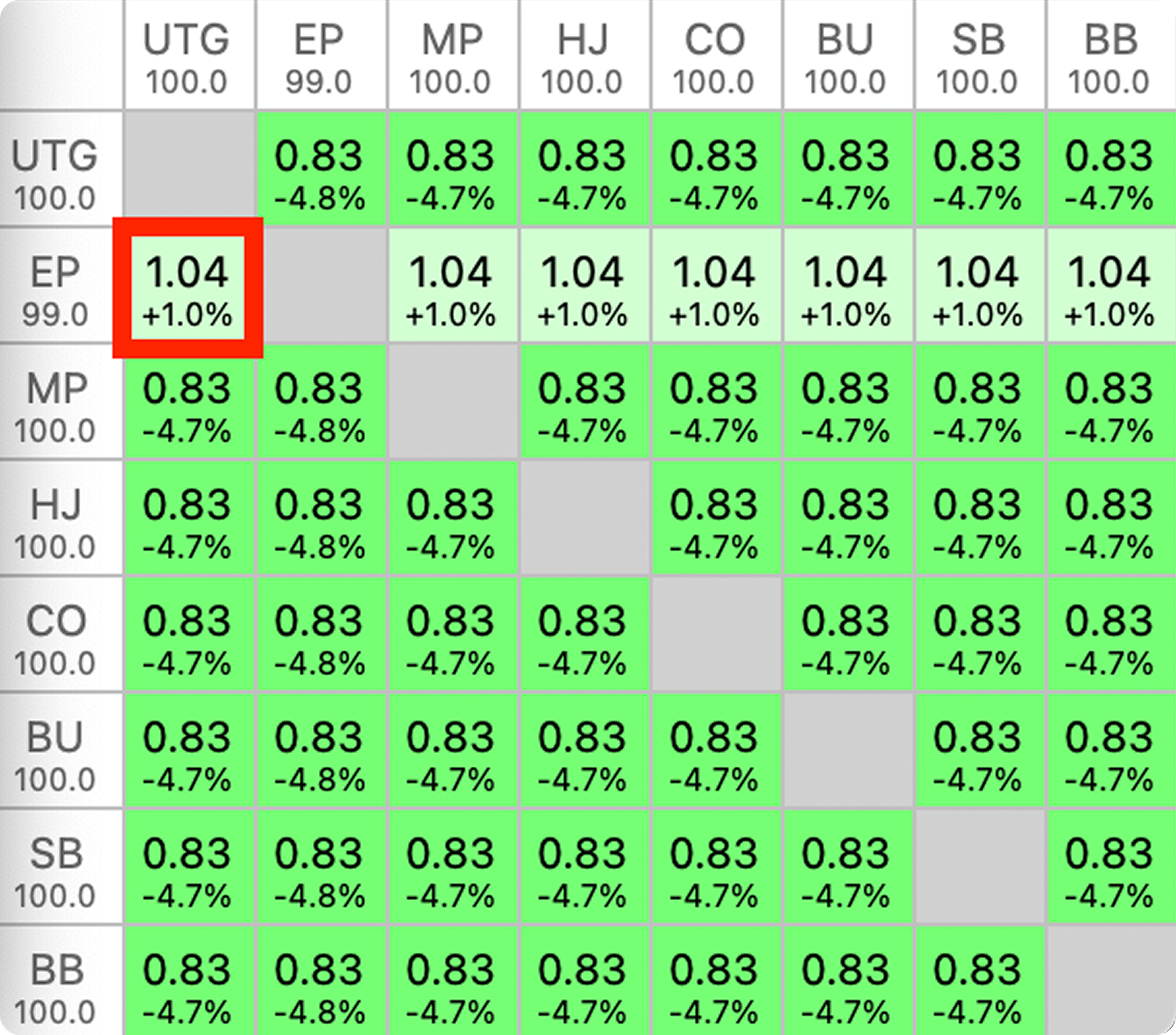
If this hypothesis holds true, we would expect to see an approximately 25% decrease in ICM risk premiums in a 25% SKO. Similarly, a 75% reduction in ICM risk premiums in a 75% SKO. Curious? Well, I ran some simulations, and the data is in. Below are the bubble factors for a 25% and 75% SKO with the same tournament parameters as the previous examples above:

BFs & RPs (%)

1000-runner MTTs: 2nd hand 25% SKO → 2nd hand 75% SKO: 1000/1000 runners remain

Now, the covered EP player with 99bb shows a 1.0% risk premium in the 25% SKO25% ($100+$33.33) SKO:
The Bounty Bubble Factor (BF) for the EP player in the 25% SKO is calculated as follows:
—
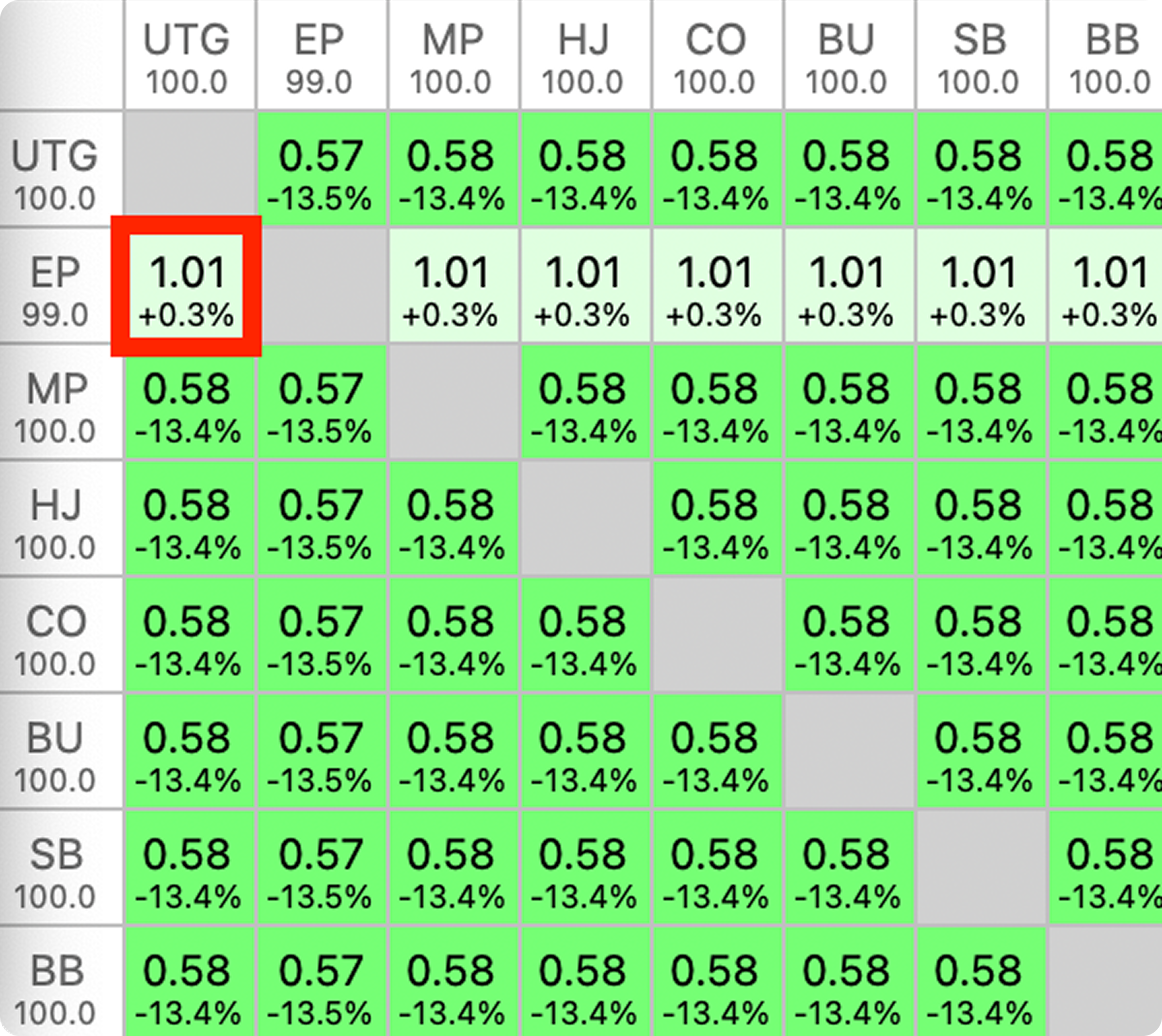
The Theory of Bounty Tournaments – Part 3: Key Calculations
—
The ICM risk premium for EP vs UTG in the SKO with the small 25% bounty is 1.0359%, or 74.49% of the risk premium in the regular MTT. As expected, the EP player’s risk premium is reduced by 25.51%, slightly more than 25%. and a .3% risk premium for the 75% SKO75% ($100+$300) SKO:
Similarly to the 25% and 50% SKOs, we expect that a 75% bounty will decrease the risk premium experienced in a similar regular tournament by slightly more than 75%.
—
The Bounty Bubble Factor (BF) for the EP player in the 75% SKO is calculated as follows:
—
The Theory of Bounty Tournaments – Part 3: Key Calculations . Breaking down the exact math, indeed the new risk premiums are also reduced by slightly more than the expected 25% and 75% of the ~1.4% ICM risk premium in the regular non-bounty MTT. Please see the notes included in the above two tooltips associated with the (RP) values if you would like to examine the calculations.

Hypothesis: The proportion of the entry fee that goes to the bounty prize pool corresponds with the reduction in total risk premium pressure.

In summary, just as it is possible to calculate the bounty value in chips or equity drop by the ratio of the bounty to the total entry fee, it is also possible to anticipate approximately how much ICM risk premiums will be reduced in the bounty MTT with the same information. This formula breaks down deeper in the tournament as factors such as ICM pressure changes. We still do see lower overall risk premiums in bounty tournaments throughout the tournament than in regular MTTs, but exactly how much won’t always correlate so easily as it does at the start of the tournament.

Series Wrap-Up

As this article concludes the deep dive into the impact of the addition of a bounty prize pool in MTTs, let’s recap the key takeaways from this series:

The regular prize pool in a bounty MTT is distributed by placement in the tournament and is modeled by ICM, similar to a non-bounty MTT.
The bounty prize pool, however, is not distributed by placement and thus follows a Chip EV model.
Bounty payouts generate a negative risk premium pressure that’s exerted on the bubble factors of the players. This negative risk pressure is called an equity drop. The equity drop is the difference between what the ICM risk premium would be in a similarly structured tournament if there were no bounty prize pool and the total risk premium with the value of the bounty and bounty prize pool future EV factored in.
The positive ICM risk premium associated with the regular prize pool and the negative equity drop associated with the bounty prize pool approximately add up to a player’s total RP (bubble factor).
The value of the bounty expressed in chips and the value expressed in an equity drop risk premium % are theoretically the same. If we plug the bounty value in chips into the pot odds formula, the difference between the odds with and without the bounty value in chips = the equity drop. It’s purely a matter of preference if we want to think of and/or calculate bounty values in terms of chips or as an equity drop as they are simply different ways of conceptualizing/expressing the same value.
The value of the instant bounty that can be won, expressed in either chips or equity drop, is the same for all covering stacks. Covering players will all win the same instant $bounty amount, and their future bounty EV share will all increase by the same amount as the decrease of the future bounty EV of the eliminated player.
The ICM risk premium for each covering player (originating from the regular prize pool) is the primary force that shapes the difference in the bubble factors (total risk premiums) vs. a covering stack since the value of the bounty is the same for all covering players.
At the beginning of a tournament, the ratio of the instant bounty $value to the total entry fee (after rake) can be used to quickly calculate the following two metrics:

•

The start value of the bounty expressed in terms of equity drop or chips.

•

The amount of the decrease in the total risk premiums (bubble factors) of covered stacks in a bounty tournament vs. a classic tournament with the same structure.

Many of the optimal strategy adjustments that solvers demonstrate in bounty MTTs are tied to how the operator structures the tournament and buy-in. A thorough understanding of these fundamentals makes it relatively quick and easier to know where and how to adjust at the beginning of the MTT. It also offers a starting point from which a player can build a cohesive plan for the rest of the tournament.

Author

Dr. K

Dr. K (aka drkamikaze) is a passionate researcher, theorist, and teacher who has been playing MTT poker for over 20 years. They are a coach at the PokerMix, specializing in ICM and bounty tournaments.

Wizards, you don’t want to miss out on ‘Daily Dose of GTO,’ it’s the most valuable freeroll of the year!

Sharpen Your Game With Our Most Customizable GTO Trainer Ever

We Are Hiring

We are looking for remarkable individuals to join us in our quest to build the next-generation poker training ecosystem. If you are passionate, dedicated, and driven to excel, we want to hear from you. Join us in redefining how poker is being studied.

Check out the available positions here.

GTO Wizard the #1 App for Poker players

Study any spot imaginable

Practice by playing vs. GTO

Analyze your hands with 1-click

START CRUSHING NOW

JOIN DISCORD