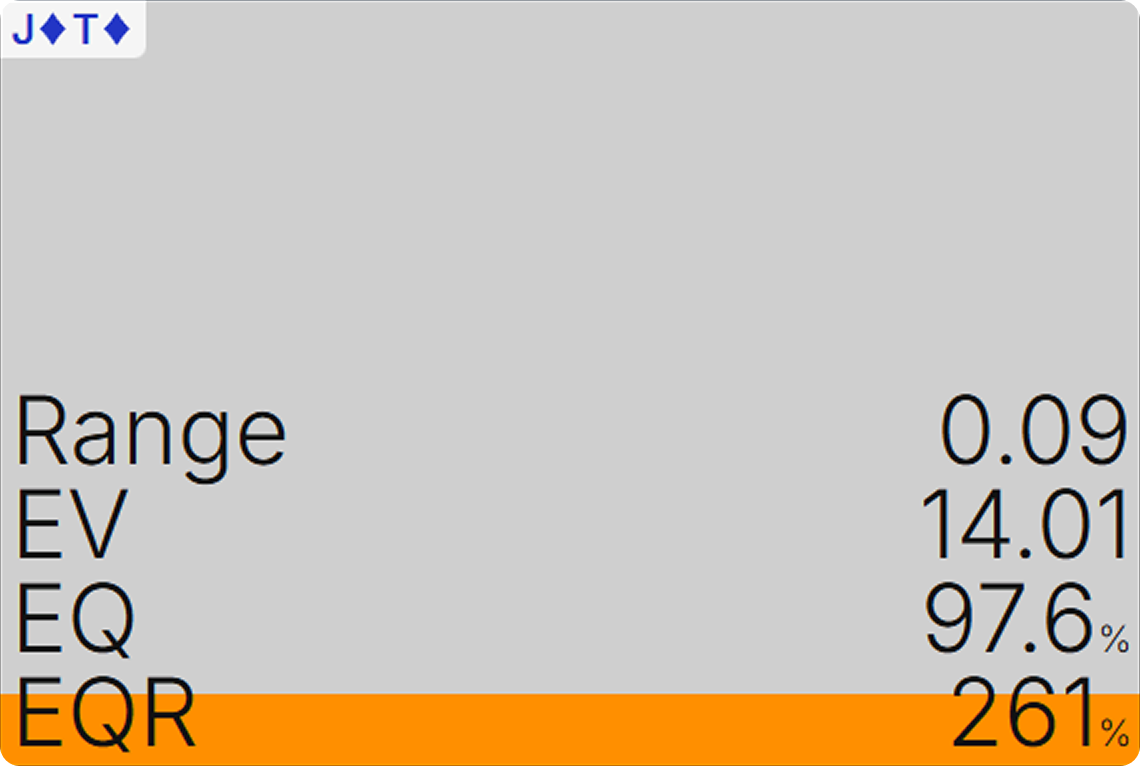What’s Your Hand Worth?
From Thin Value to Playing for Stacks
Poker theory offers many conceptual tools for answering the question, “What is your hand worth?” You may be familiar with equity (EQ), expected value (EV), and equity realization (EQR), which are essentially different methods of taking a snapshot of a hand’s value. If someone offered you cash in exchange for your share of the pot at this exact moment, before any more cards are dealt or bets are placed, these tools could help you determine what that cash value would be.
But that’s not how poker works. You can’t just freeze the action mid-hand, take your equity, and move on to the next one. Actually, some games offer “all-in insurance,” which, for a bit of vig, enables you to do exactly this. But commonly, the question you’re most interested in is not, “What is the theoretical value of my hand at this exact moment?” but rather,
“How much more money should I be willing to put into the pot?”
This is a relevant question, whether you are considering betting for value yourself or calling a bet from another player. And it’s a tricky question to answer for a few reasons:
- The answer depends on your opponent. This is the crux of poker, the thing that makes it a more interesting game than solitaire. If your opponent will only put money in with very strong hands, then you’ll need a strong hand to put money in yourself (unless you can benefit from fold equity). If they will put money in with weaker hands, then so can you.
- The answer changes as you receive new information in the form of new community cards or actions your opponent takes. But, as we will see, the answer may depend less on this new information than you think!
In theory, the volume of money you put into the pot—we’ll call this “betting volume” from now on—with your range should not depend terribly much on how the money goes in or how the board runs out. That’s a complicated statement, so let’s break it down.
A player’s betting volume should not depend terribly much on how the money goes in or how the board runs out.
First, what does “volume of money” mean? Here’s an example: There’s $100 in the pot on the flop. Your opponent bets $100. You call with 50% of your range and fold the rest. On the turn, they bet pot again, which is now $300. You call with 50% of your current range (the hands still remaining after you called the flop) and fold the rest. On the river, they bet pot one more time, putting you all-in for $900. You again call with 50% of your current range and fold the rest.
We can break your starting range into four chunks:
- 50% of your range folds the flop and so puts $0 into the pot.
- 25% of your range calls the flop and folds the turn, putting $100 into the pot.
- 12.5% calls flop and turn but folds river, putting $400 into the pot.
- 12.5% calls all the way to showdown, putting $1300 into the pot.
Total Betting Volume = (50% * $0) + (25% * $100) + (12.5% * $400) + (12.5% * $1300) = $237.50
Now, suppose your opponent checked the flop, bet $300 (into $100) on the turn, and then shoved the river for $1000 (into $700). You, believing they would not have checked a strong hand, decide to respond stubbornly and once again call with half your range on each street despite the much worse pot odds offered by these overbets.
- 50% of your range folds the turn and so puts $0 into the pot.
- 25% calls turn but folds river, putting $300 into the pot.
- 25% calls all the way to showdown, putting $1300 into the pot.
Total Betting Volume = (50% * $0) + (25% * $300) +(25% * $1300) = $400
Your opponent has put the same amount in with their hand, but your range puts much more money in, on average, when they start by checking the flop. What incentives does this create for your opponent? How could they exploit your strategy?
When your opponent has a nutty hand, they’d prefer the second line that starts with a flop check. That will result in them winning $400 (or a bit less—maybe a few of your very strongest hands beat them) on average, while the geometric strategy would win them $237.50 on average. When they have a weak hand, however, they’d prefer the first line that starts with a flop-bet.
In other words, if you respond like this, your opponent is not indifferent to betting the flop. They strictly prefer betting weak hands and checking strong ones.
Consequently, this cannot be an equilibrium. If your opponent were to play that way—always betting the flop with bluffs, always checking strong hands—then you could unilaterally improve your EV by getting stubborn against their flop-bets and folding when they bet after checking the flop. That, in turn, would incentivize them to stop bluffing the flop and start c-betting their strong hands. Betting volume is one of the five fundamental imbalances of poker.
In order to make your opponent indifferent between various betting lines, you must ensure you are not rewarding them for choosing one line over the other with any type of hand. That means you must put roughly a proportionate amount of money into the pot regardless of the betting line your opponent chooses.
I say “roughly” because you can and should respond to changes in board texture. For instance, when the flush draw comes in, the specific hands with which you will bet or call a bet will be different than those on blank rivers. And even the volume could change somewhat depending on whether the new board card is especially good or bad for your range. But changes based on your opponent’s betting line—paying off with more or less of your range based solely on how they put the money in—are exploitable.
Value Planning
One implication of this is that you can get a rough idea, as early as the flop, of how much money you should be aiming, or at least willing, to put into the pot with your hand. The closer it is to the top of your range, regardless of its absolute strength, the more you should look to put in. If your hand gains or loses value as a result of a change in board texture, then you can reassess and change plans if appropriate.
This principle applies just as much to making your own value bets as it does to defending against your opponent’s bets. Another aspect to highlight is that players focus too much on the decision immediately in front of them: should I bet this street, and if so, how large?
Before answering that question, however, it’s useful to zoom out and look at the big picture: how much do I ultimately want to put into the pot, across all remaining betting opportunities? Is this hand currently worth my entire stack? How likely is that to change?
When and how much you bet matters a bit, but more important is how much money you ultimately put in.
As we have seen, the volume of money your opponent invests ought to be roughly the same (proportionately) regardless of the betting line you choose. If you do not expect that to be the case, then you can consider how to take advantage of those inconsistencies. But mostly, you want to focus on how much you can compel your opponent to invest with a range of hands you’ll be ahead of.
This is easiest to see with the nuts. When you flop the nuts, you should almost always be thinking about how to get your opponent’s entire stack into the pot. The major exceptions are highly dynamic boards where, for example, top set could easily be supplanted by straights and flushes as more cards are revealed. But usually, it’s better to start with the goal of playing for stacks and then reevaluate if the board texture changes, rather than playing defensively in fear of potential board changes.
Introducing a Hand Example
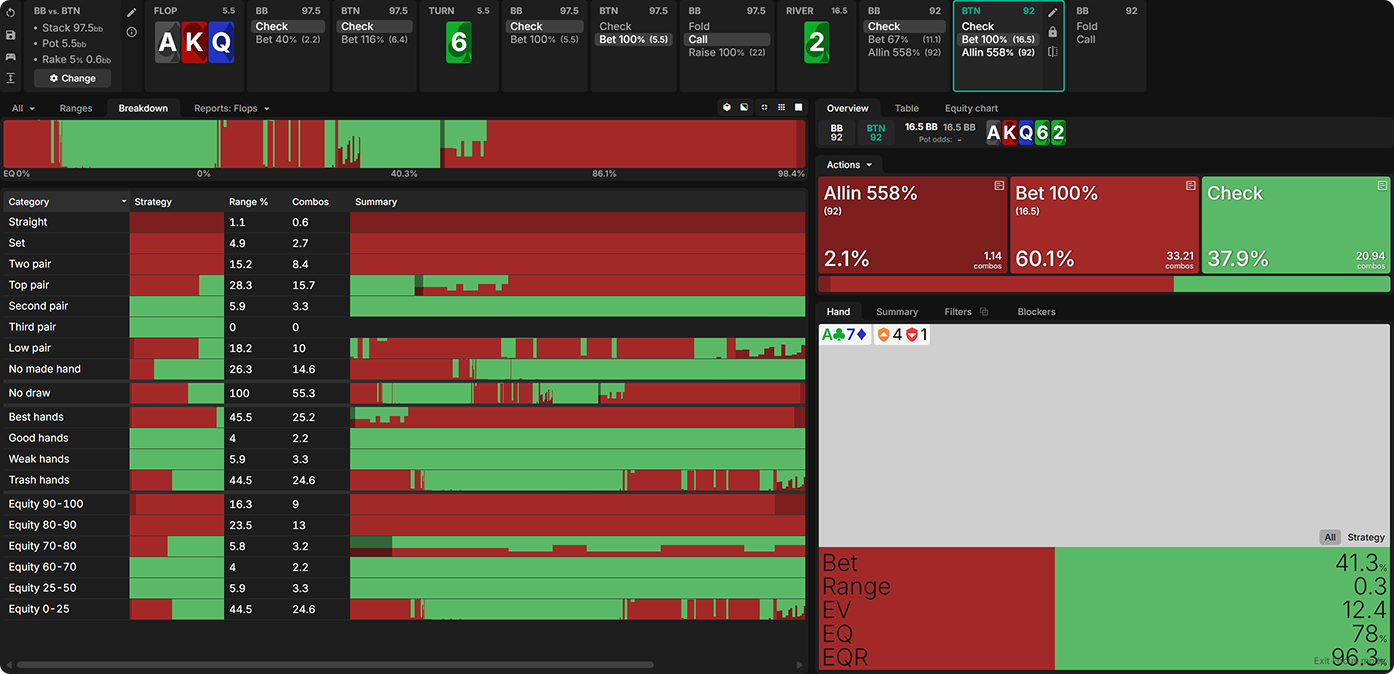
Suppose you’re playing a 100bb cash game. You open the BTN with J♦T♦, BB calls, and you flop the nuts on A♠K♥Q♦. BB checks.
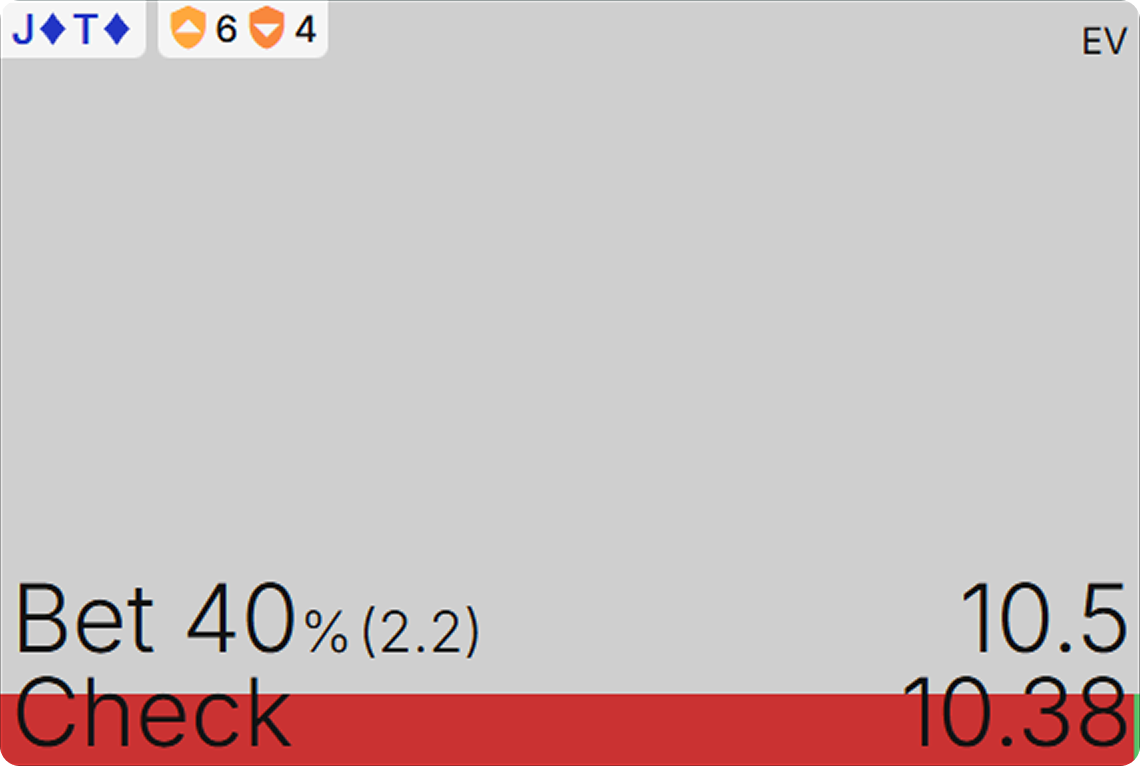
The presolved sim shows you as roughly indifferent between checking or betting any of four different sizes:
You might look at what a small sliver of the strategy checking makes up and how the EV of checking appears to be a few hundredths of a big blind less than the best bet sizes, and conclude that betting is better. I’m inclined to agree.
These slight variations are due to convergence errors. These simulations have a small margin of error, which is why the solver shows a mixed strategy even though one option appears to have a higher EV. I would conclude from this that the options are extremely close at equilibrium, and while a large c-bet does appear to be slightly better than the other options, the best choice in a real-life game situation will depend on how you expect your opponent to respond to different bet sizes.
For our purposes, what matters is that checking is at least nearly as good as betting 125% pot. In a custom sim with just a single bet size option, J♦T♦ appears indifferent between betting and checking when it flops the nuts:
This is because you can make up the difference later. In other words, when it does not bet the flop, the solver will want to bet blank turns and then jam most rivers. This will ultimately put just as much money into the pot as a geometric bet-bet-shove line, and it will incentivize your opponent to invest roughly the same volume of money.
After checking the flop, the custom sim purely bets the turn. Even here, however, the EV difference is not enormous. Betting is 1.2% better than checking.
There is a limit to this, however. If forced to check the flop and turn with JT, the solver never shoves the river for 1773% pot.
New Information
It’s worth asking why, if betting volume matters more than the betting line, J♦T♦ has declined in value after not betting the flop despite seeing a neutral turn card. It sure seems like missing that flop-bet has cost us 1.3bb, more than 10% of the EV we flopped.
The neutral turn card is not the only new piece of information we have received that’s caused us to update the value of our hand.
One of the many possible outcomes baked into the EV displayed on the flop is BB aggressing into our nuts. When we bet the flop, that would take the form of a check/raise. When we check the flop, it would take the form of a turn-bet.
The EV loss is the result of learning that our opponent does not have a hand with which they wish to bet the turn. After the 6♣ is revealed as the turn card but before BB acts, the EV of J♦T♦ is in fact higher than it was on the flop, even though we have foregone our first opportunity to grow the pot.
The EV gain here is the result of fading the worst turn cards—the ones that would change the board texture. Board pairs are bad because we will no longer have the nuts, but Jacks and Tens are quite bad as well. Even though they don’t change the rank of our hand, they create many scenarios where we chop large pots and reduce our opponent’s incentive to invest in hands we’re ahead of.
When we learn that the turn card is not one of these worst-case scenarios, our EV rises. But then, we learn that BB does not wish to bet the turn and our EV declines.
What Are “Nut Hands”?
In the early days of no-limit, “the nuts” referred to literally the best possible hand. It’s still used that way today, but it’s also taken on a broader meaning of any hand strong enough to invest your entire stack into the pot. How do you know when your hand is effectively the nuts so that you can start building the big pot you want?
Now that we know your opponent’s betting volume should be roughly the same regardless of how the money goes in, we can get a rough idea of which hands they will stack off with by testing how they would respond to an all-in bet. Even when the solver would not expect to face such a bet at equilibrium, it still provides an unexploitable response. The hands they stack off with when all the money goes in at once should be roughly the same ones they’d stack off with if all the money goes in across two or three streets on a relatively blank runout.
If your hand is ahead of that stack-off range, then you should be trying to get all the money in. Of course, that doesn’t mean you just move all-in immediately. Your opponent will have other hands that call one or two bets (or bluff into your checks) but eventually fold, and you’d like to get paid by these as well. So, shoving is usually not the optimal way of putting a stack in before the river, but it’s a useful tool for assessing whether that should be the ultimate goal.
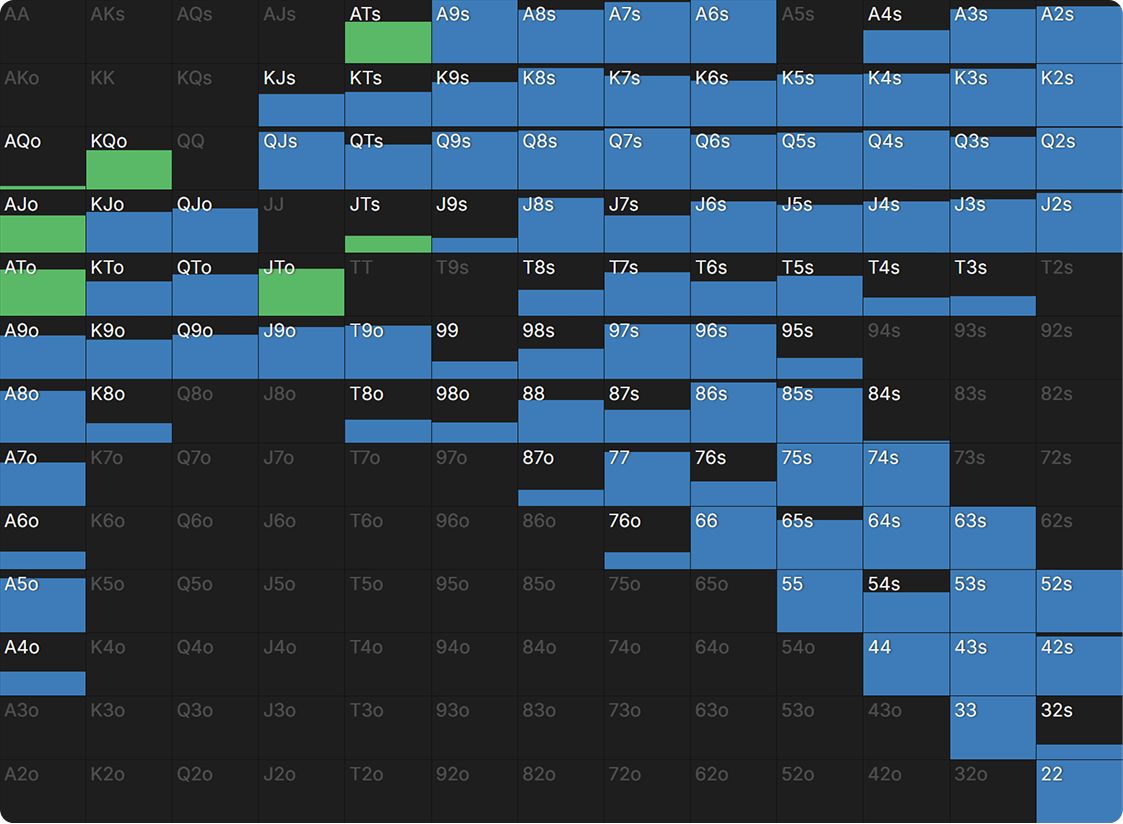
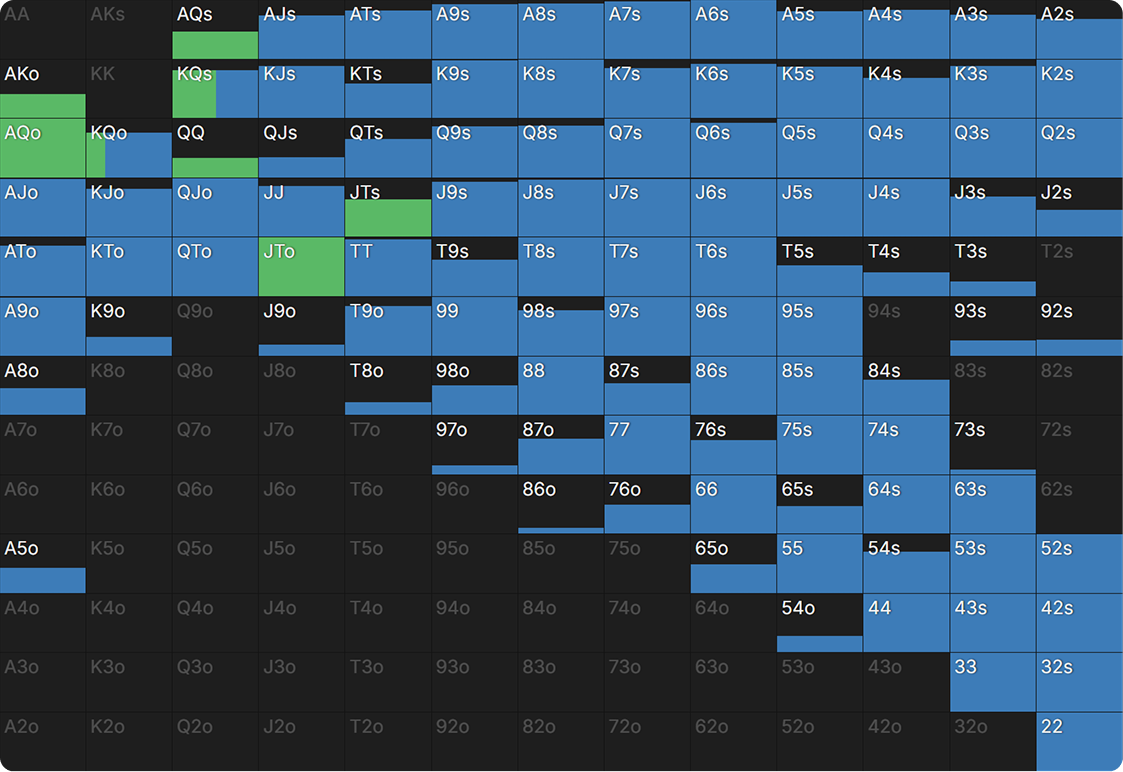
For example, here’s BB’s stack-off range if BTN were to shove the AKQ flop:
With such a high SPR, only the very best hands are worth their stack. The bulk of BB’s stack-off range is top pair with a gutshot (and, importantly, straight blocker), so it looks like BTN will need something stronger than top pair to jam for value.
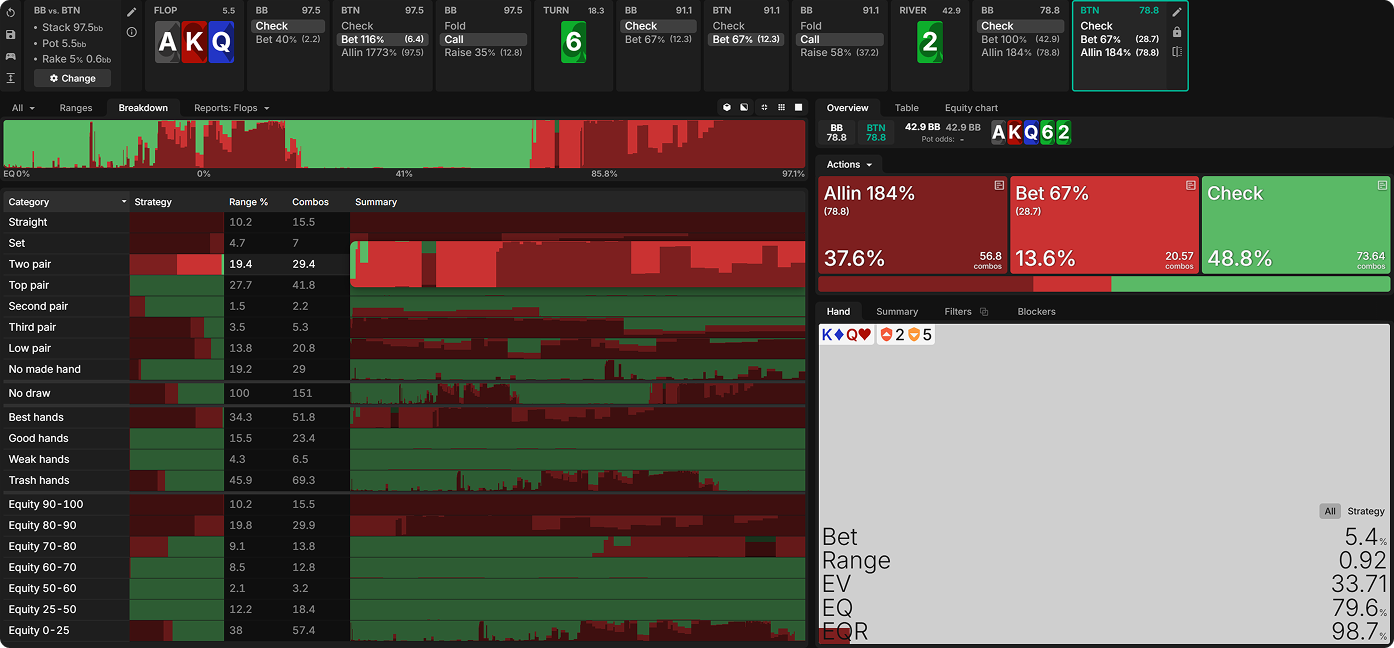
Sure enough, if we check BTN’s range for going bet-bet-shove on AKQ62, the worst hand they jam for value on the river is KQ:
Stack-off ranges are not based on the absolute strength of hands but rather on where they sit relative to both players’ ranges.
If this were a BB vs UTG confrontation, both players would see the flop with strong ranges. BB would have an even stronger stack-off range, and UTG would need an even stronger hand to shove for value. Remember point (1) from the introduction.
Thin Value
You don’t need the literal or effective nuts to bet for value. Your opponent’s range for calling one or two modest bets will be wider than their stack-off range, so you should also have hands that bet one or two streets for value even though you aren’t trying to get stacks in with them. These hands may also benefit from the protection value of denying equity, but that’s not the primary reason to bet them. When you have a good hand, you mainly profit by making bets your opponent is incentivized to call with a range of hands you’ll be ahead of.
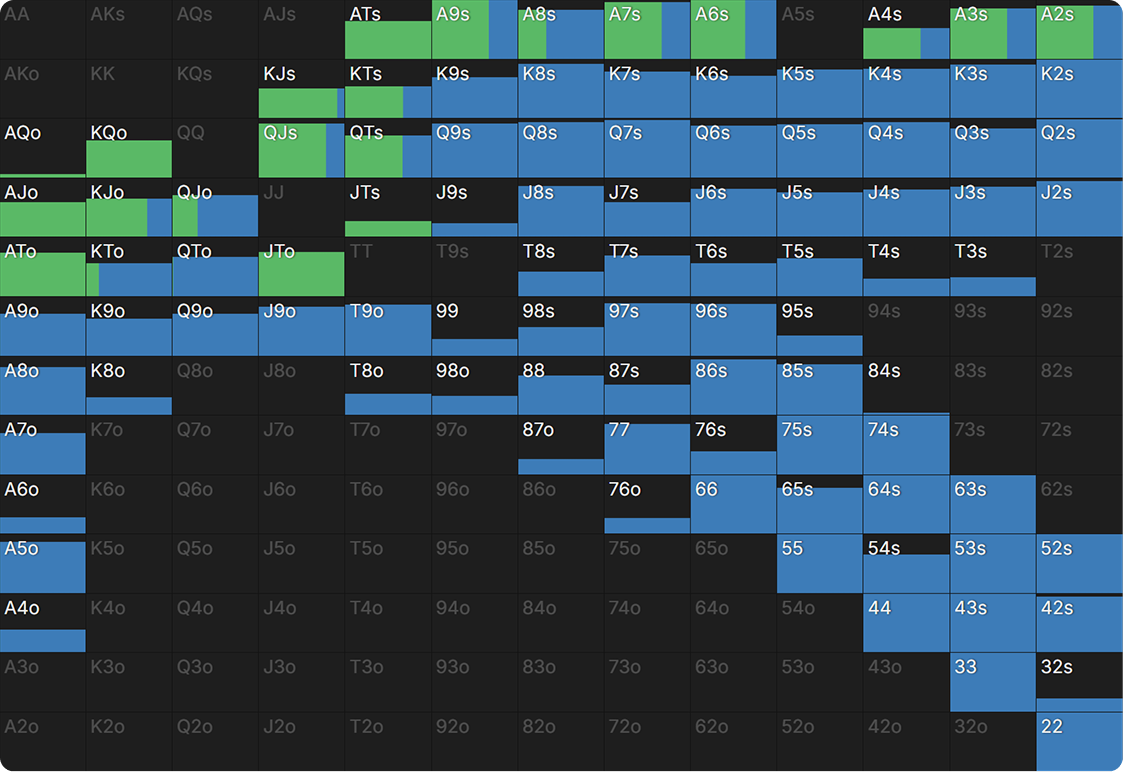
We can use the same technique to get a sense of the opponent’s range for putting smaller amounts into the pot, even if those amounts are split across multiple streets. Editing our BB vs BTN custom solution to replace the all-in bet with a 400% pot bet and removing BB’s option to raise (which would complicate the results) provides a sense of what we’d be up against if we made two pot-sized bets (or three smaller bets that result in the same pot size).
This range contains many more top pair hands but doesn’t stop there; the solver reaches further down with some second and third pairs with straight draws (and straight blockers). The straight draws complicate things a bit because on blank runouts these will become less desirable calling hands, but we can glean the basic idea that this range is much heavier on one pair, especially top pair, than BB’s stack-off range was. So, if we can beat top pair, even if just with top pair and a better kicker, that’s probably worth two pot-sized bets (or three smaller ones, or one 4x pot bet).
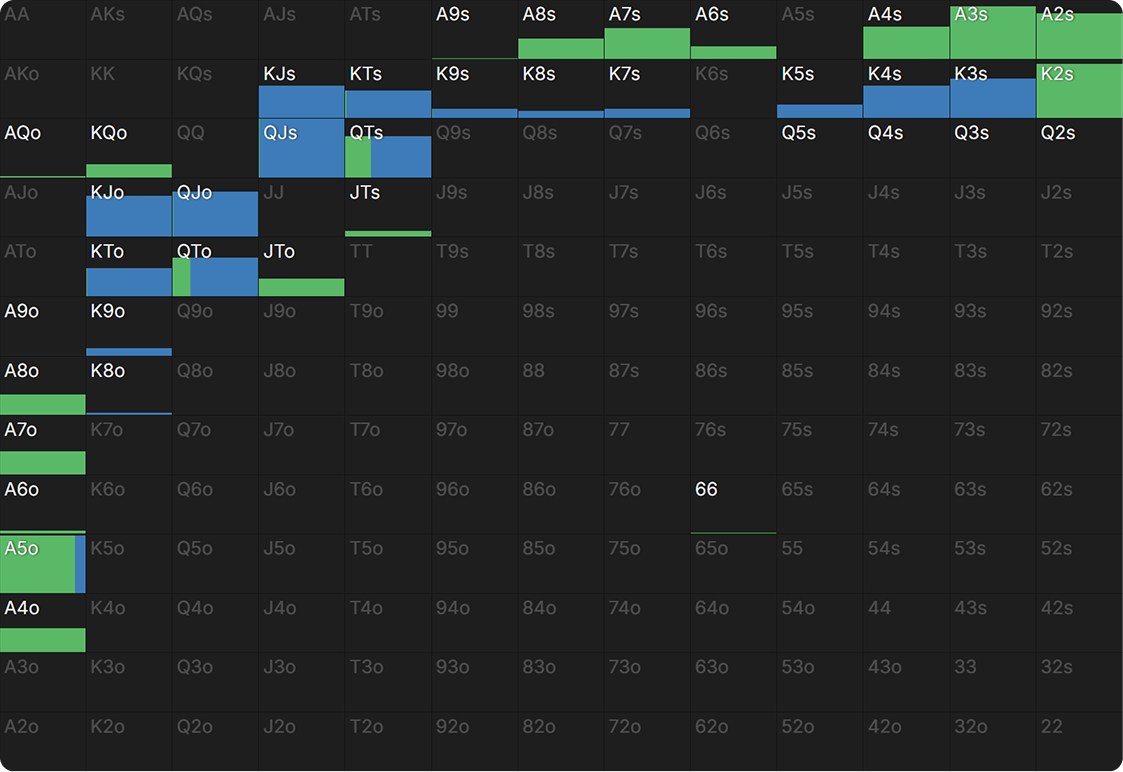
Here’s the BB’s range for calling river after BTN checked the flop and then bet pot on the 6♣ turn and 2♣ river (as before, BB is not given the option to raise):
As predicted, most of those second and third pair hands drop out of the calling range once they lose the straight draw and are replaced by more top pairs. The weakest hand with which BTN pots the river in this scenario is A7. It’s not nearly strong enough to play for stacks (which would be a 558% pot bet), but it beats the weaker top pair with which BB is incentivized to call a smaller 100% pot bet:
Conclusion
You won’t be able to conduct such experiments in real time at the table, but by making them a regular part of our off-the-felt study, you can build intuition around how much you should be trying to invest with various hands in various scenarios. Having an overall objective for the hand provides additional information and context for the individual decisions you’ll make during the hand, such as, “Should I bet the flop? If so, how large should I bet?”
Boxer Mike Tyson is often quoted as saying, “Everybody has a plan until they get punched in the face.” Hopefully, no one is actually punching you over a poker game, but sometimes an unexpected check-raise or ugly river card feels like a fist to the face.
When something unexpected occurs, it’s time to revisit your plans. The beauty and the tragedy of poker is that sometimes hands that were very strong, hands you were counting on to win you multiple large bets or even an entire stack, lose some of their value when the unexpected happens.
As you get better at planning, you can start incorporating these risks into your plans. Sometimes, it makes sense to prioritize betting early streets in case your hand loses value. Sometimes, it makes sense to bet draws on early streets in case they turn into value hands later.
The only sure thing in poker is that the cards and your opponents will find ways to foil your plans. When they do, it’s time to reassess and ask yourself anew, “Now what is my hand worth?”
Author
Andrew Brokos
Andrew Brokos has been a professional poker player, coach, and author for over 15 years. He co-hosts the Thinking Poker Podcast and is the author of the Play Optimal Poker books, among others.
We Are Hiring
We are looking for remarkable individuals to join us in our quest to build the next-generation poker training ecosystem. If you are passionate, dedicated, and driven to excel, we want to hear from you. Join us in redefining how poker is being studied.