Building Better River Strategies
(And When to Ignore Equity Advantage)
To frame today’s article, let’s start with a question: “What is the principal characteristic that differentiates the river from the flop and turn?”
Hint: It’s something that’s marked by a feeling of anticipation.
One of the major things to anticipate when you find yourself on the flop or the turn are the cards still to come. Once you reach the river, the board is complete; there are no more new cards to be dealt. This difference requires you to take a different approach—from that of the flop and the turn—when building a river strategy.
This article will explore two essential concepts crucial for mastering advanced river strategies:
- Cropping Ranges – Betting the river against the defending player’s weakest hands makes no sense (since there is no more value to be gained from denying for protection). By disregarding the trash, we are effectively “cropping” their range to zone in on the remaining (stronger) range that is relevant to our betting strategy.
- Equity Inflation – When they fold those weaker hands, their continuing range contains a higher proportion of strong hands, increasing their average equity against the bettor’s range. In this way, their “equity inflates,” but our equity also deflates.
Often, toy games are used to analyze and understand why an equilibrium strategy looks the way it does. However, there are spots where the equilibrium strategy is relatively challenging to understand, and resorting to toy games only wouldn’t be enough. For this case study, we will grab some toy games from the shelf, but we will supplement them with various other concepts so we can learn how to handle equities and EQ graphs more precisely.
For our analysis, we will be using GTO Wizard with the following parameters: 6-max, 100bb, 50nl, GTO-GTO.
Case Study #1
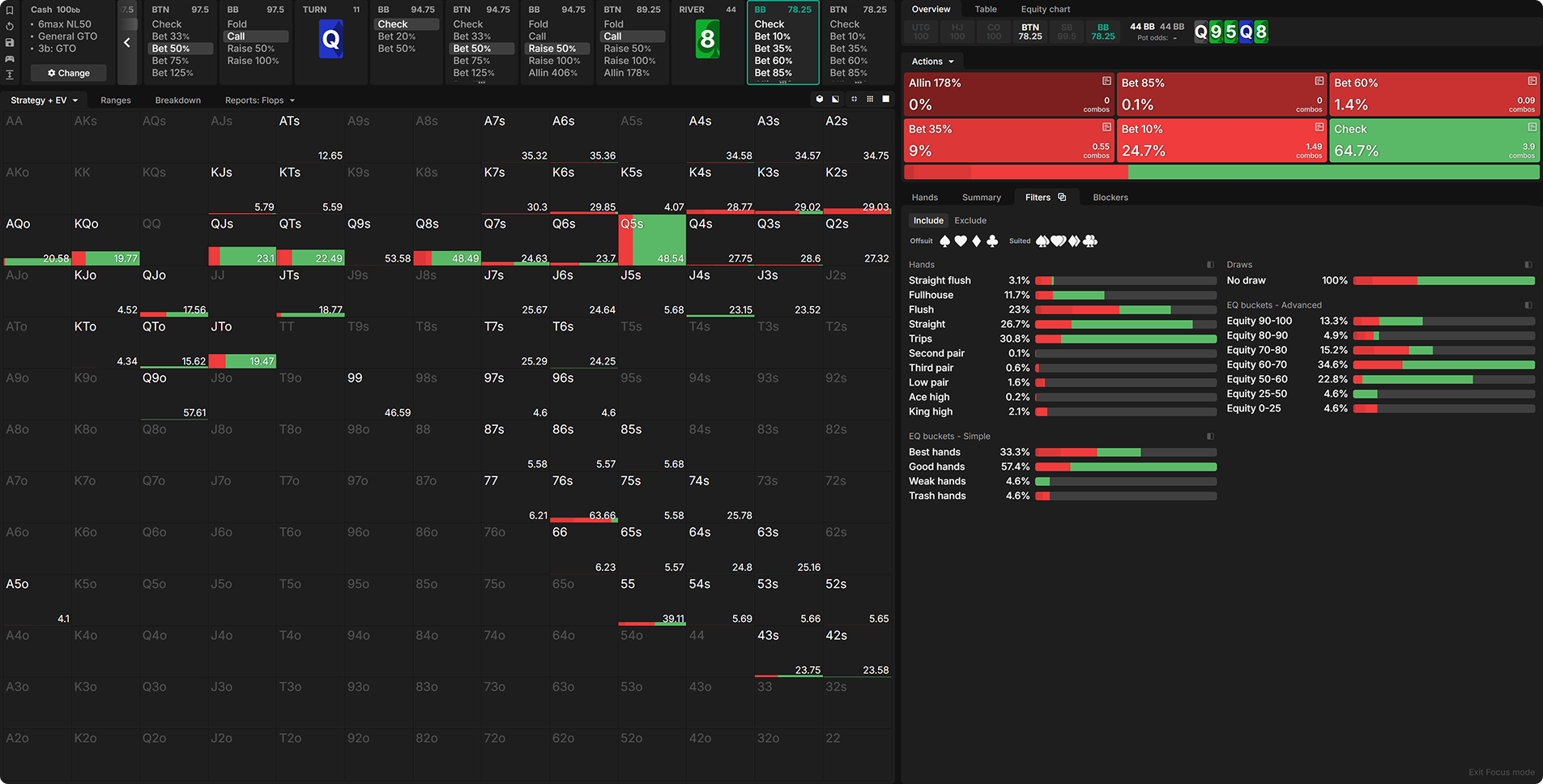
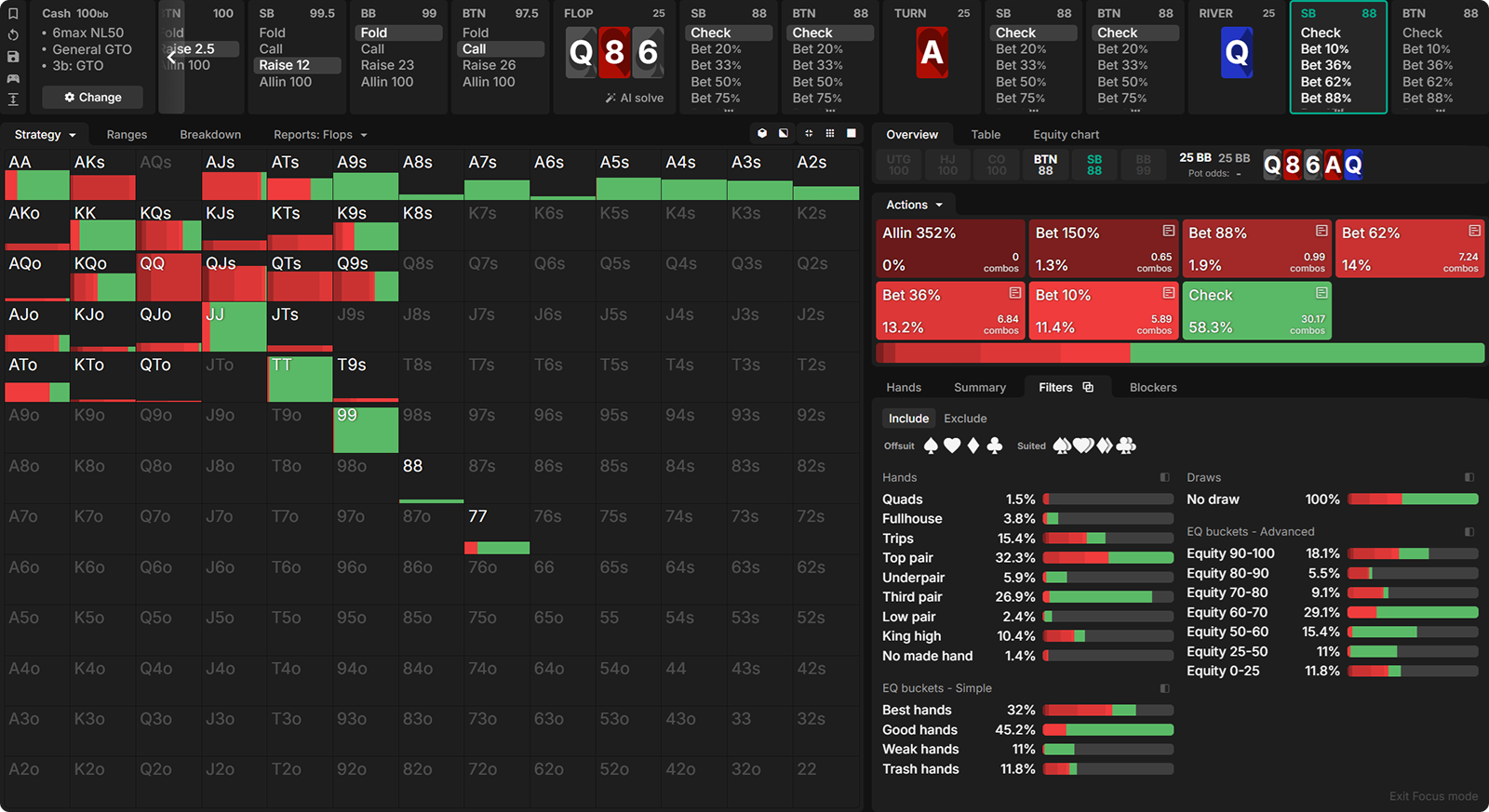
The following hand captured the attention during a study session with friends:
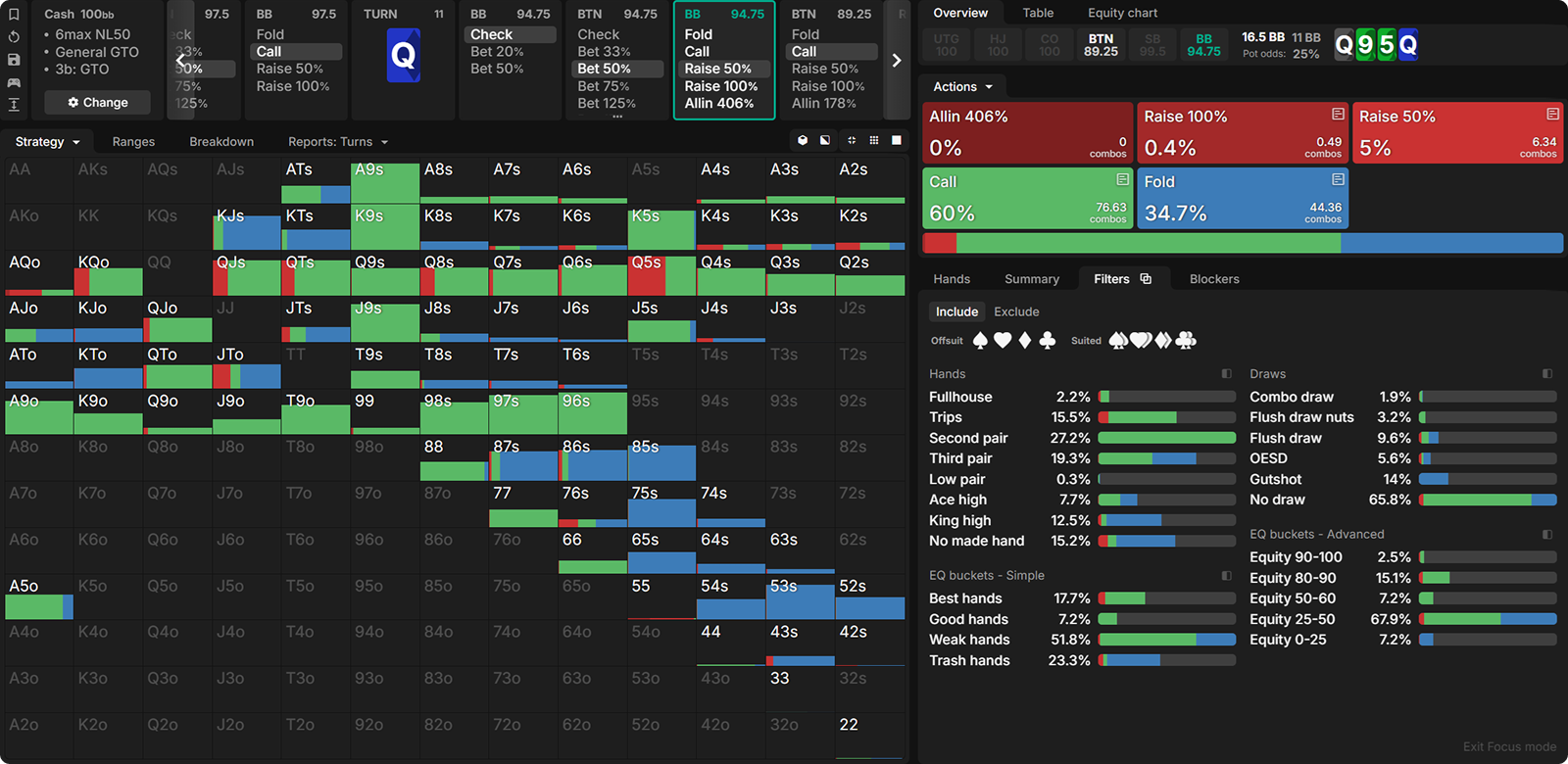
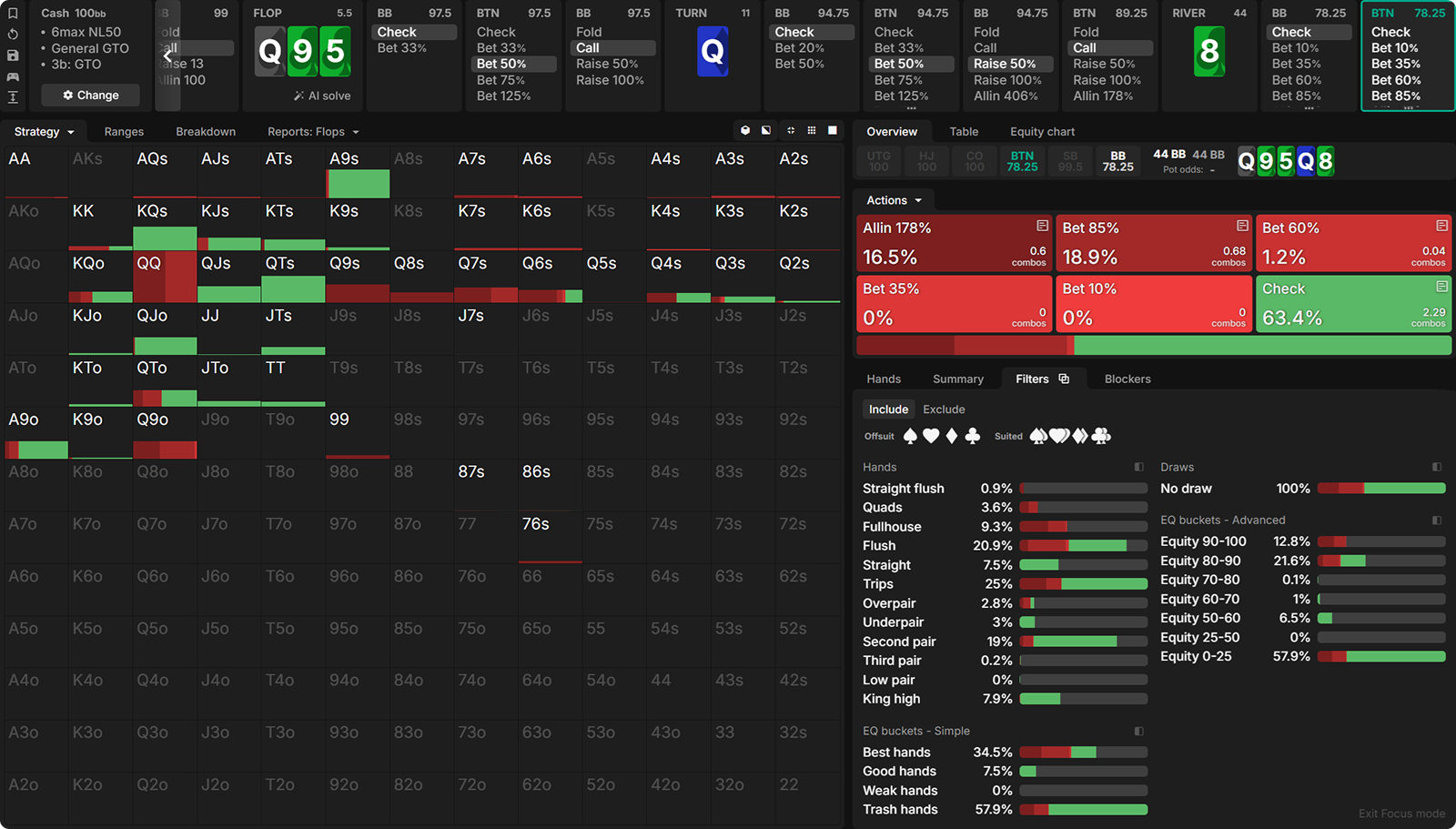
- Preflop: BTN open-raises, BB calls.
- Flop: Q♠9♣5♣. BTN c-bets 50% pot, BB calls.
- Turn: Q♦ pairs the board. BTN bets half-pot again, BB check-raises, BTN calls.
- River: 8♣ completes various draws. Action is on the BB.
What kind of strategy should the BB employ with their range? Which hands should be bet? What about sizings? Pause for a moment and think about the answers to these questions.
In order to fully comprehend this spot, you first need to know and understand the equity of both players.
Understanding the Equilibrium
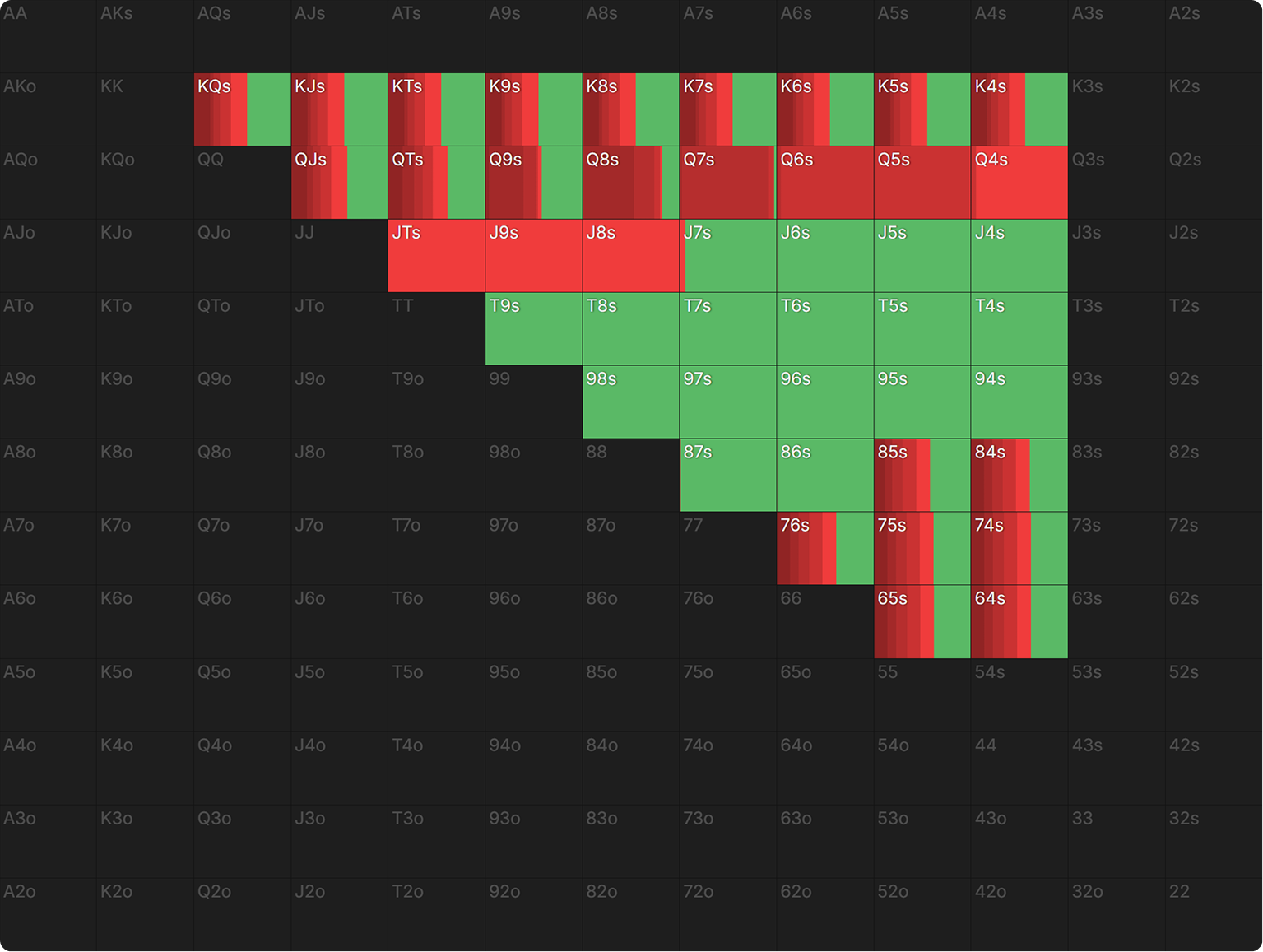
Let’s translate the BB’s actions to their range at equilibrium. By calling the BTN’s flop c-bet, the BB removes the absolute trash from their range. On a board-pairing turn Q♦, they change to an aggressive stance by check-raising.
They never do so with a 9 or 5; they’ve got at least a Queen for trips in their value range. The raising range is balanced with bluffs, such as flush draws and straight draws—especially the open-ended straight draws and combo draws. Since no-pair hands with one high card, such as K4s, would not have called the flop c-bet unless it had a flush draw, the check-raises from such no-pair hands on the turn are strictly flush draws.
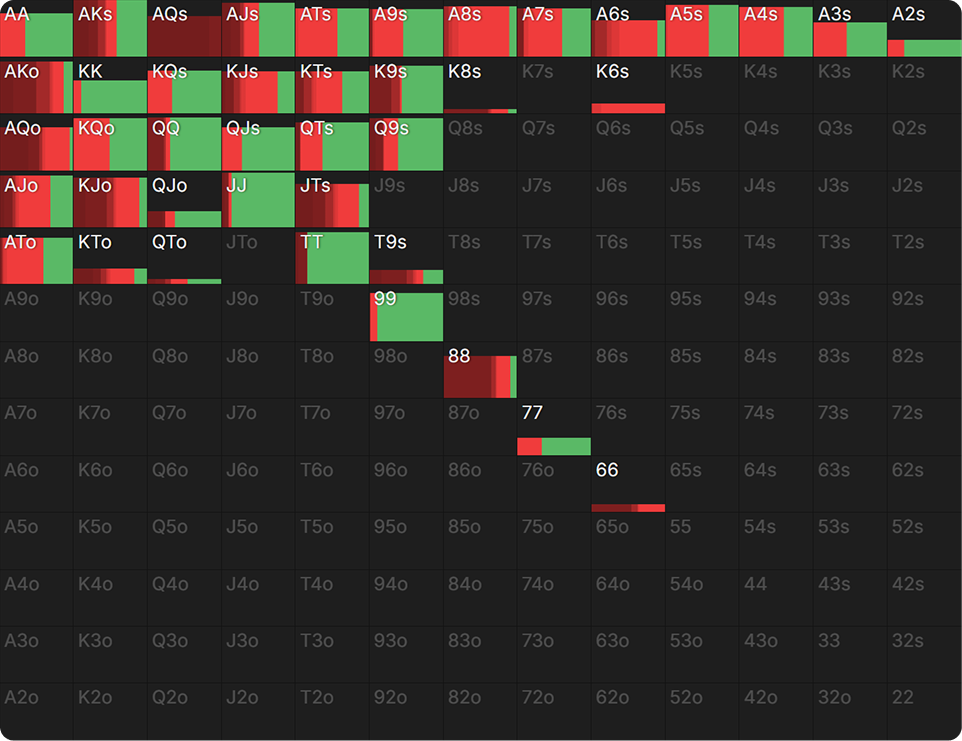
After a super wet river 8♣, what does the BB’s range look like? All of the flush and straight draws that semi-bluffed the turn are now completed. So, the BB has at least trips or better. How about the BTN? They cannot have air, given that they double-barrelled and called the turn-raise.
The BTN very well may have a flush or trips as well, but they could also have a pair of nines or a pocket pair that were considered marginal against the turn check-raise. Although the BTN’s range isn’t entirely hopeless, it does contain weaker hands compared to the BB’s range, which only consists of trips or better.
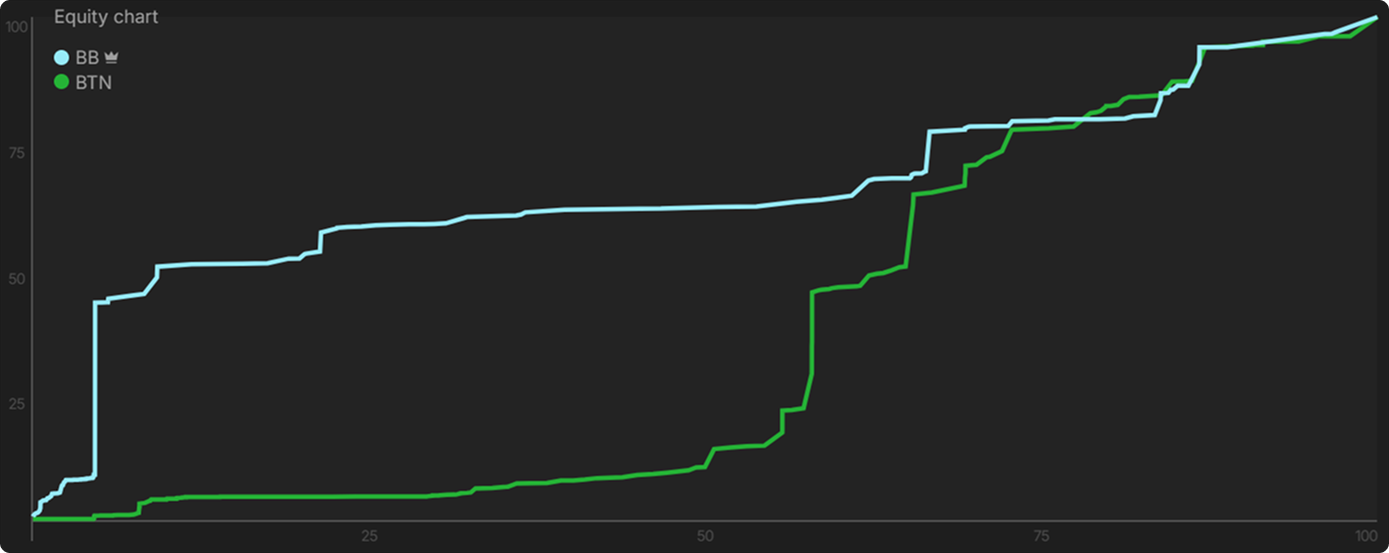
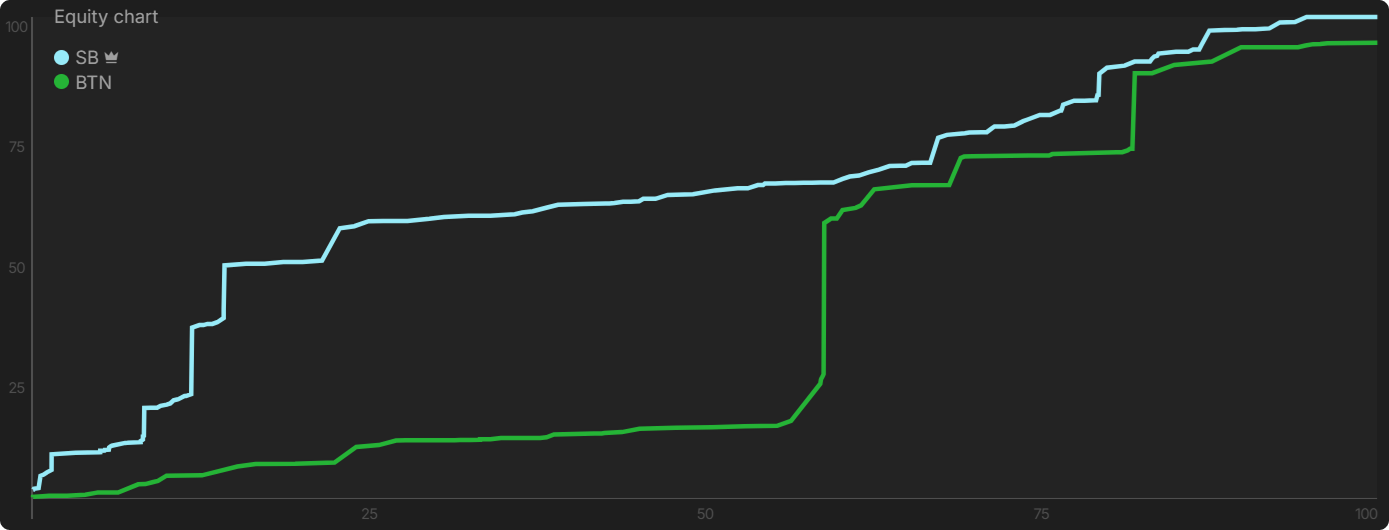
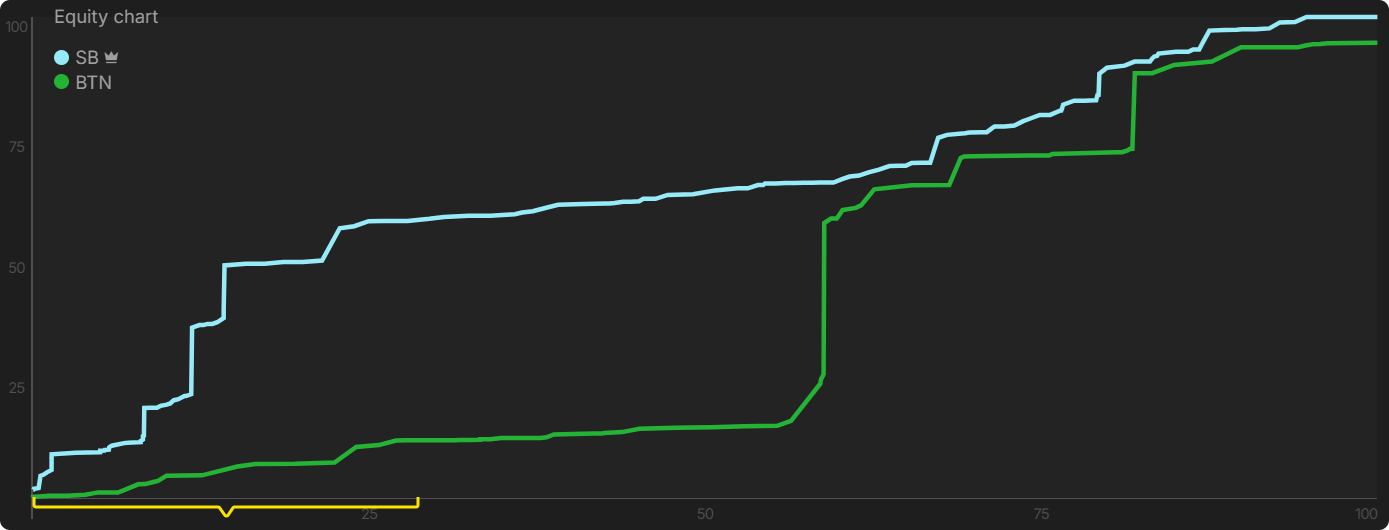
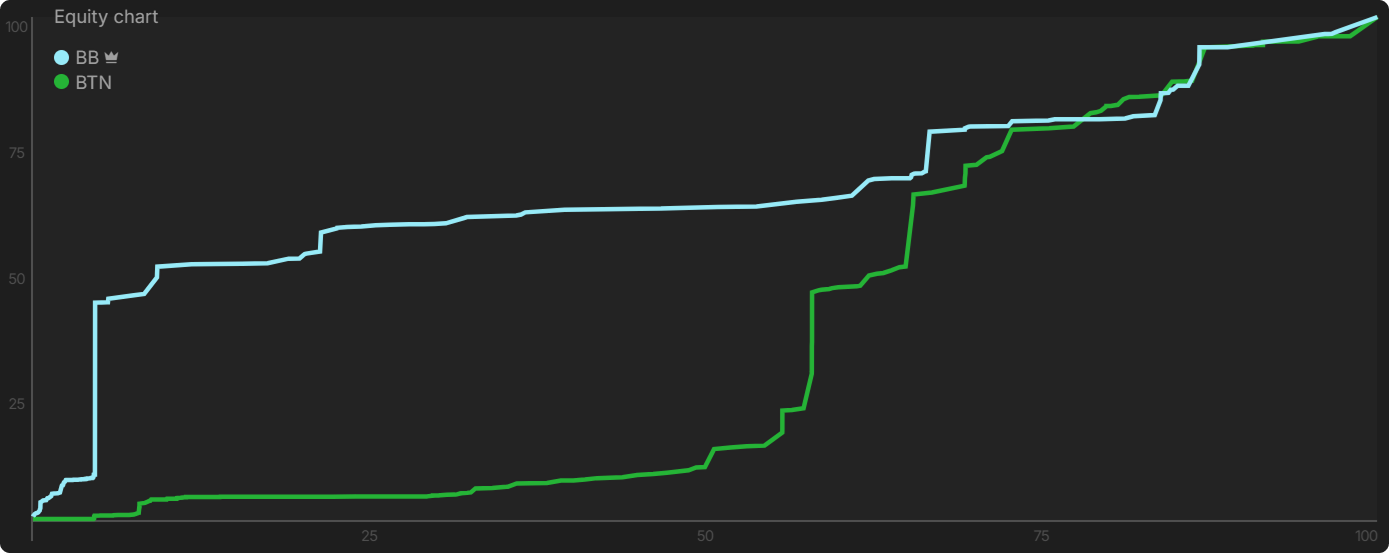
This is the EQ graph on the river. The BB has an overwhelming equity advantage with their range. The marginal holdings that the BTN called on the turn beat absolutely nothing by the river.
In light of this analysis, let’s revisit the question that prompted it in the first place.
What should the BB’s river strategy look like?
- At the very least, bet with their entire range (since range-bets often seem to occur when having a big equity advantage).
- Perhaps additionally, mix in some large bets with the stronger part of the range.
- Another strategy that features more checking. Maybe a bet big or check strategy.
Indeed, many of my friends advocated that the BB should at least range-bet.
However, the BB actually checks the majority of their range and makes a tiny bet with the remainder, despite having a big surplus in range EQ. In order to understand why the BB is employing such a strategy, we will make a short detour to the lab to pick up some necessary tools and knowledge. We will come back to this hand later. 🤯
Range-Betting With an Equity Advantage
We mistakenly presumed that an advantage in range EQ always warrants a range-bet because we often find ourselves in circumstances where this indeed holds true.
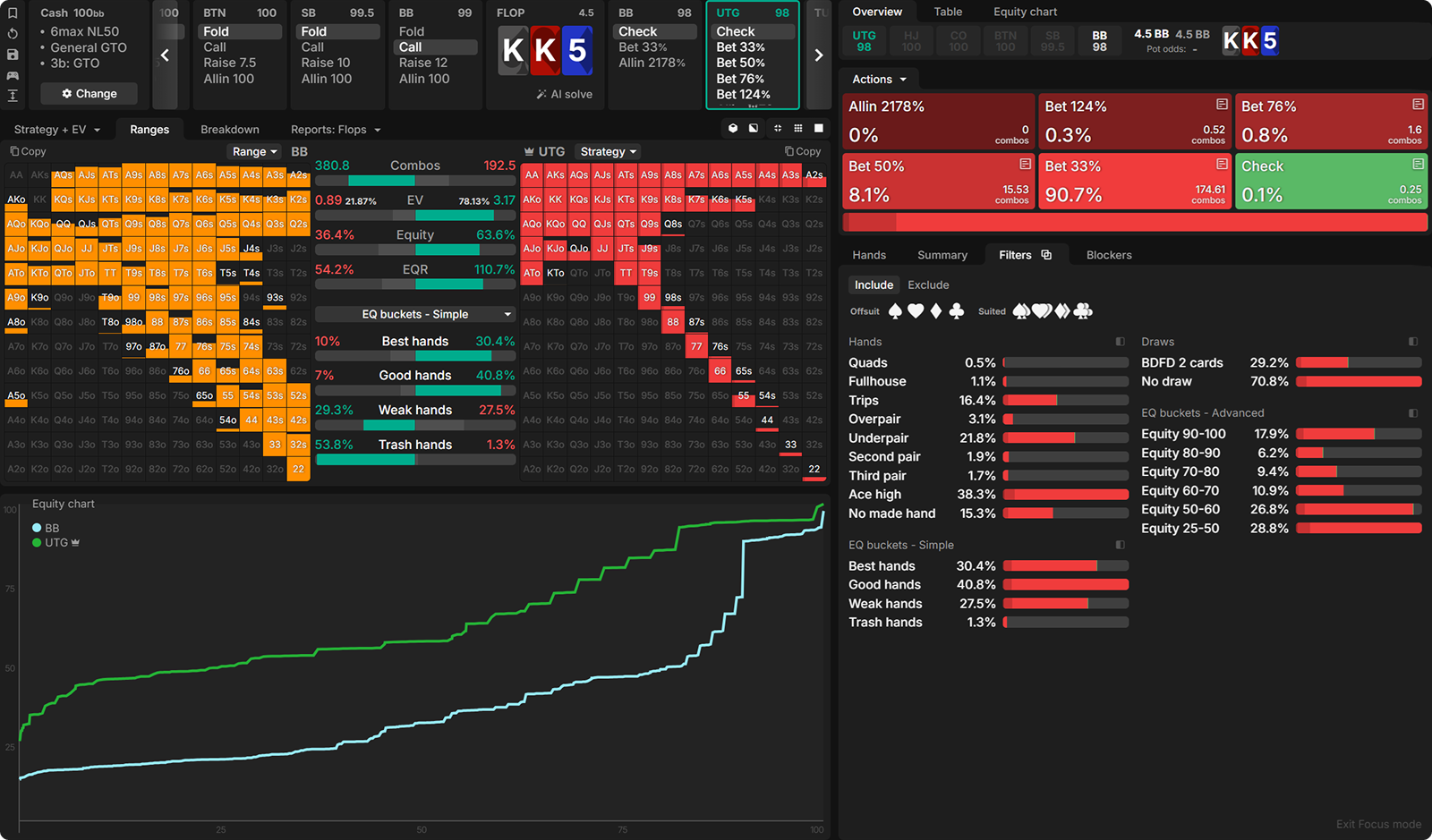
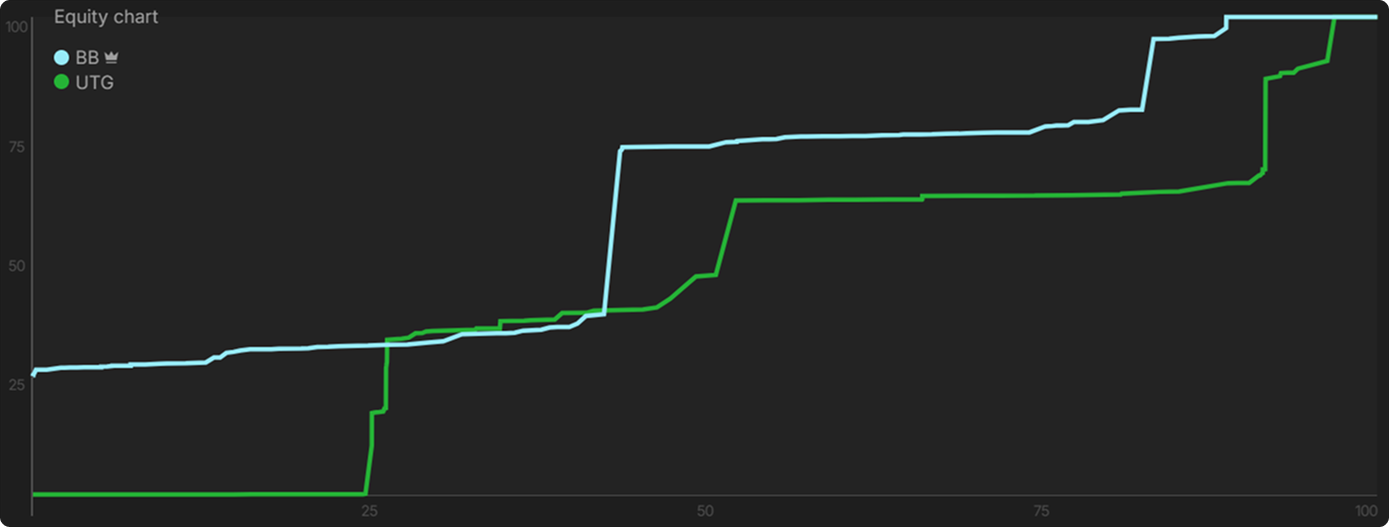
Example: BB vs UTG, SRP, KK5r
UTG’s range EQ is over 9000, uh, I mean over 63%, and we can observe them range-betting for 33% pot.
Situations like this are encountered very frequently. Then why can we not similarly range-bet in Case #1? The reason stems from the fact that these two scenarios take place on different streets.
This range-bet example above is a flop scenario, entailing that there are more cards to come. While Case #1 is a river scenario with no more cards to come. Trash hands on the flop or the turn do have some non-negligible equity, while trash hands on the river have close to zero equity. It follows that while there is some value in betting and getting those trashy hands to forfeit their equity on the flop or the turn:
Having an equity advantage is a good reason to bet at a high frequency in many situations. However, the same logic does not apply to rivers, where you must carefully determine where the point of indifference is from the perspective of your opponent.
The [0,1] Game
Next, we will study the [0,1] game to find out if there’s any insight to be gleaned from it that’s relevant to solving our main case.
[0,1] Toy Game
This toy game serves as both a theoretical and a practical model. Its setup looks as follows:
- Both players (“OOP” and “IP”) will be assigned a random number between 0 and 1.
- 0 is the weakest, and 1 is the strongest.
- Both players have an SPR of 1.
- They can bet any amount, but when they raise, it must be an all-in.
What kind of strategy do you think the OOP player will choose? If this toy game is new to you, let’s pause for a while and think about it.
You would want to bet for value when you are assigned a large number, and you would want to bluff when you are assigned a small number. If you are given a middling number, you would hope to get to a showdown by checking.
[0,1] Modeled as the KQ64-Game
We will provide the solver with the following input to analyze this toy game:
The board will be AAA 2 3 with no possible flushes. The ranges of both players will consist of unpaired, suited hands of a particular suit from 64 up to KQ—hence, this toy game is sometimes referred to as the KQ64-game. The two players have different suits.
(You could also use other constructions, such as a 222 3 3 board with ranges consisting of only pocket pairs from 44–AA.)
With this construction, we achieve an equivalent of the [0,1] game where the rank of the hands corresponds to the number assigned in the [0,1] game.
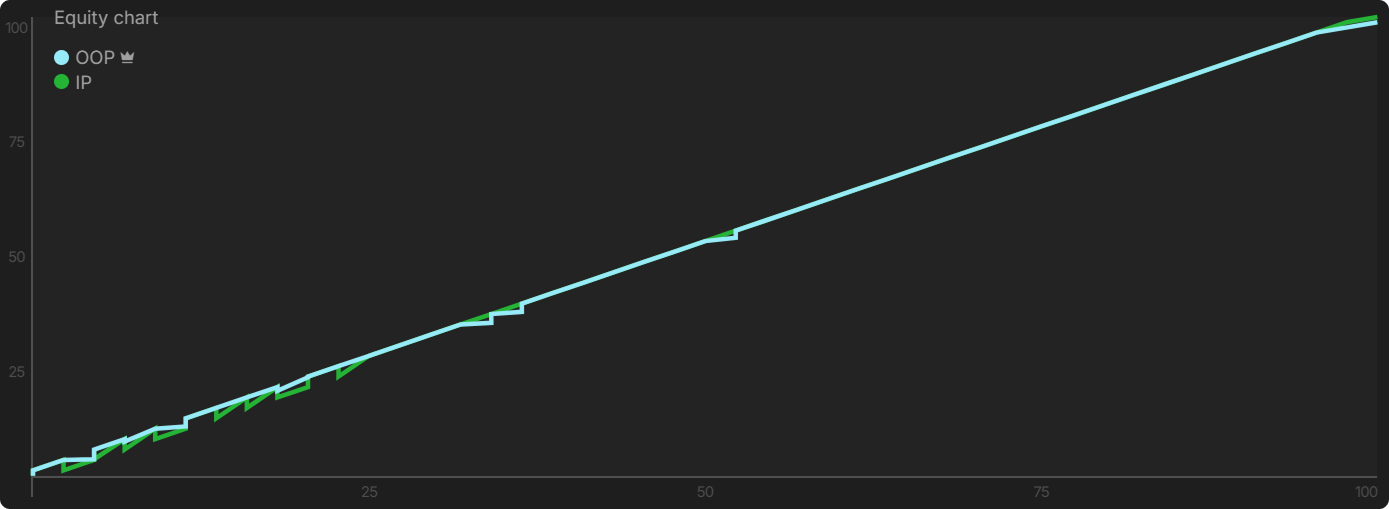
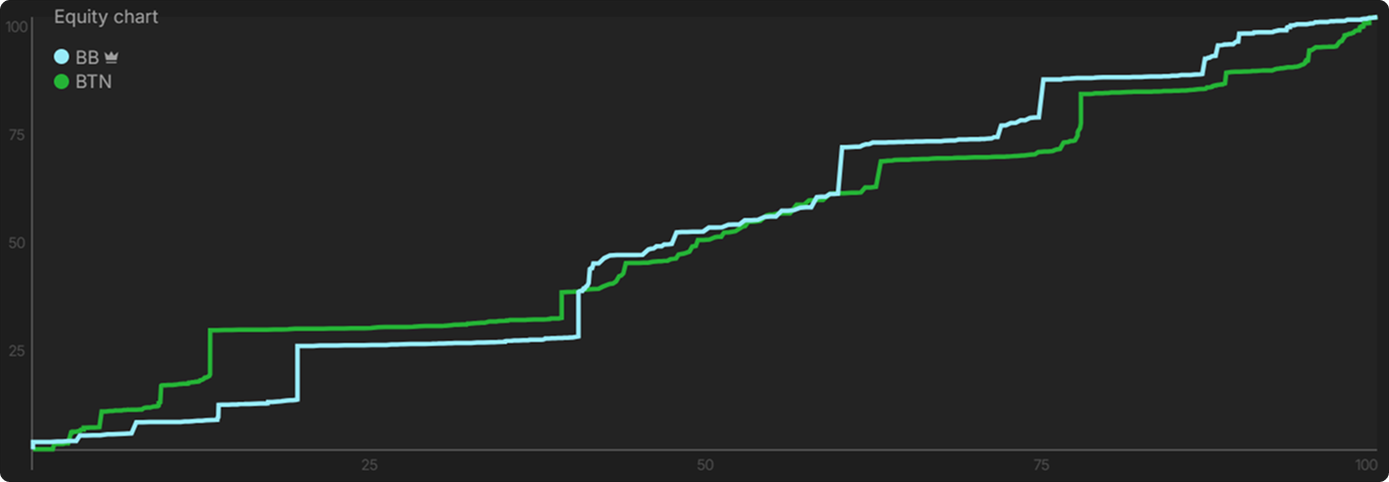
On the river equity distribution graph, only OOP’s (light blue) equity distribution is clearly visible, even though two players are mentioned in the top-left corner. So, one must overlap the other, meaning that OOP and IP have basically the same equity distribution. Their wide ranges are made up of hands with varying strength.
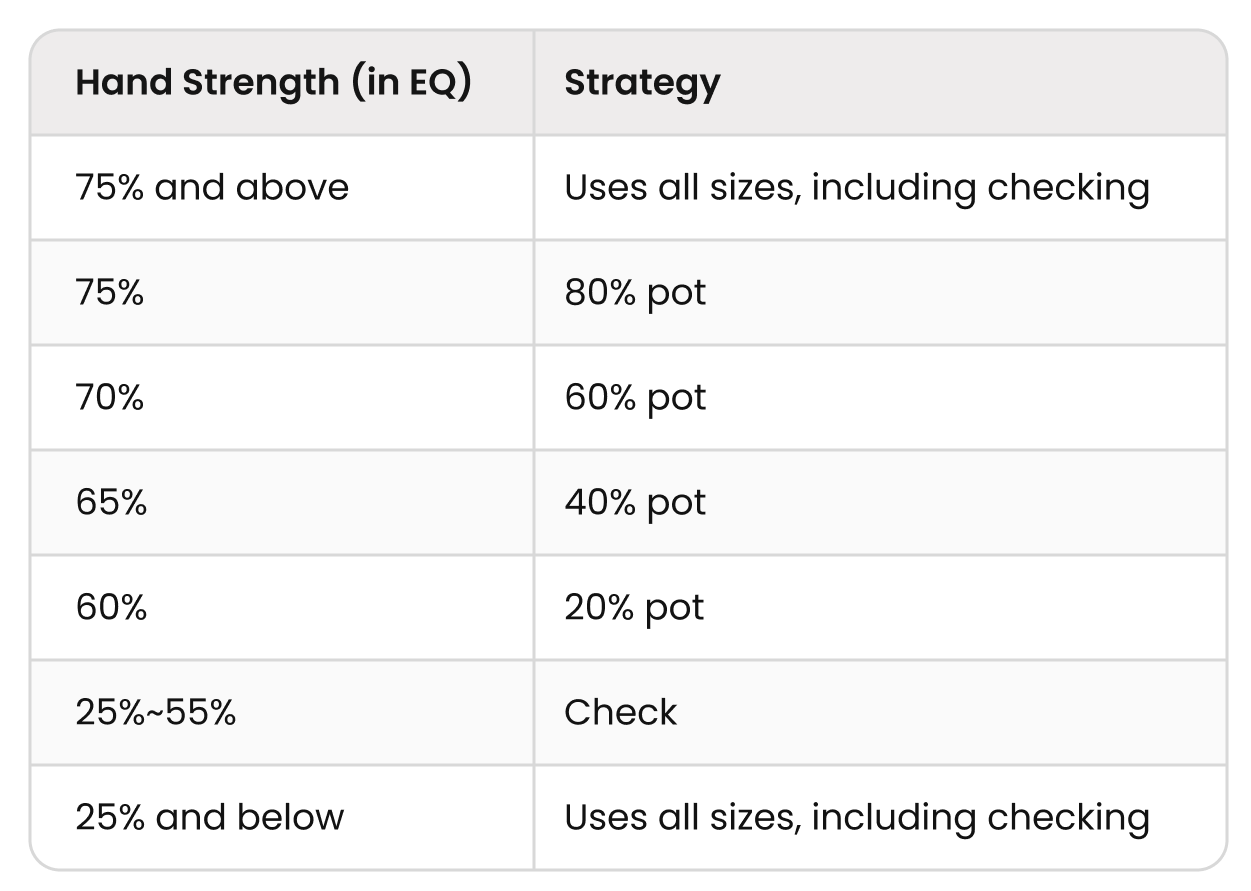
The table below summarizes the solution:
Both monster hands and trash hands use all sizesCheck can be viewed as a bet with size 0, while the hands in between only use a single size based on their equity. This strategy maximizes its EV by incorporating both monsters and bluffs in all the ranges.
Practical Application: BB vs BTN, SRP
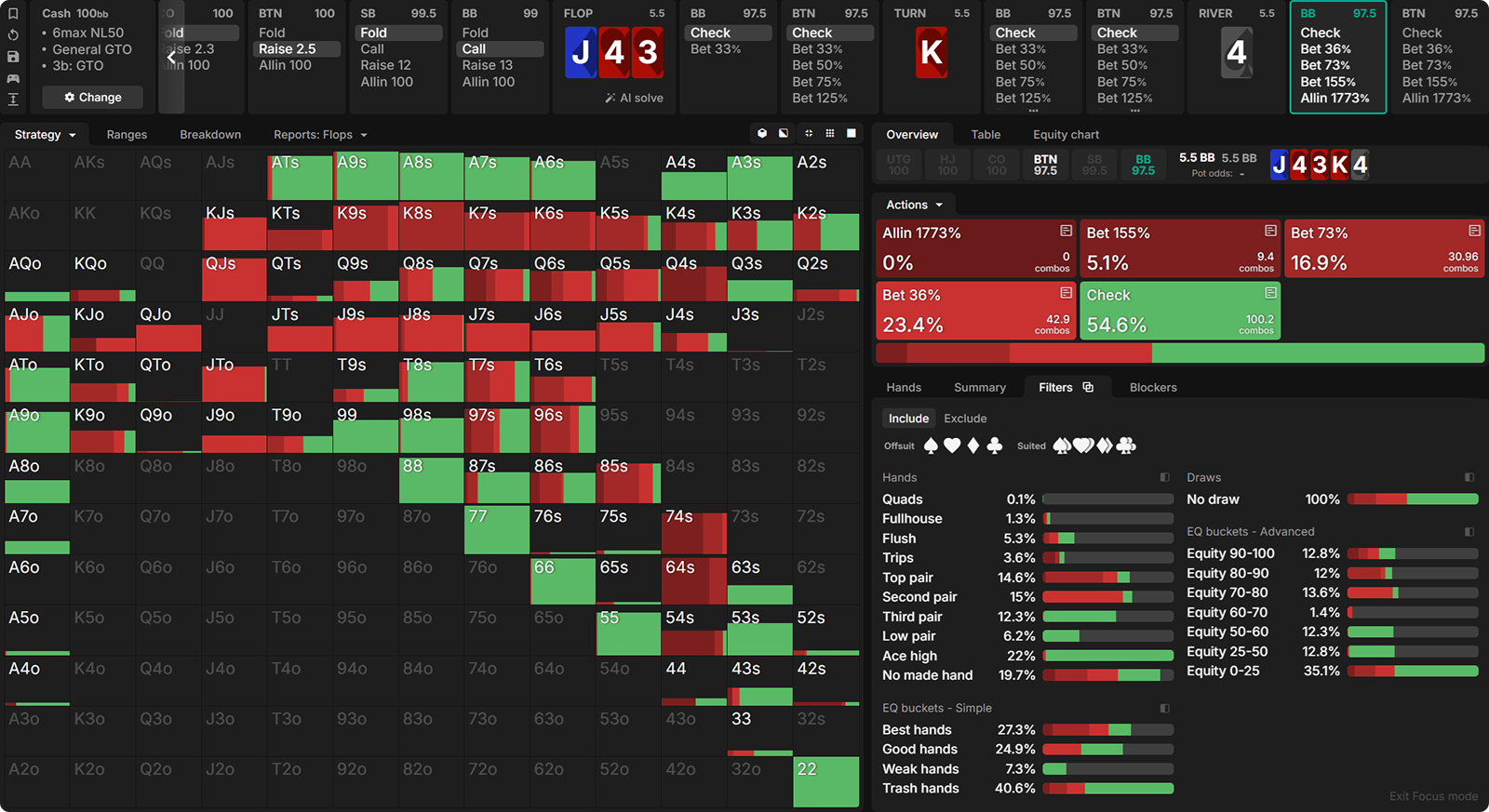
Let’s consider an SRP between the BB and the BTN on J♦4♥3♥ K♥ 4♠ where the action checks through to the river.
Both players have a wide range of hands with varying strength, just like the hand distribution in the [0,1] game. As you may have guessed, the BB will have a betting strategy similar to the one in the [0,1] game.
You might find it easier to notice the similarity with the [0,1] game via the following visualization.
In this Manhattan plot, low-equity hands are plotted on the left, and high-equity hands are plotted on the right. Do you see the striking similarity with the [0,1] game?
Now that you have an understanding of a betting strategy that resembles the [0,1] game, let us examine another case similar to Case #1, where OOP has the advantage in range EQ on the river.
Case Study #2
Here is an example of where you have a range EQ high enough on the river that a range-bet may sound plausible. It is a situation where it has been checked down to the river despite having equity advantages on the previous streets.
- Preflop action: SB vs BTN, 3-bet pot
- Board runout: Q♠8♥6♠ A♥ Q♦
- Action: Checked down to the river
Below, we have the SB strategy for the turn.
The SB has a relatively high bet frequency because the two highest cards, the Ace and the Queen, hit their range well. However, the SB also does a fair bit of checking since they do have some marginal hands in their range. When the SB does check on the turn, the BTN elects to bet 75% pot with a polar range but sometimes checks back. When the BTN decides to check back, the equity distributions on the river look as follows:
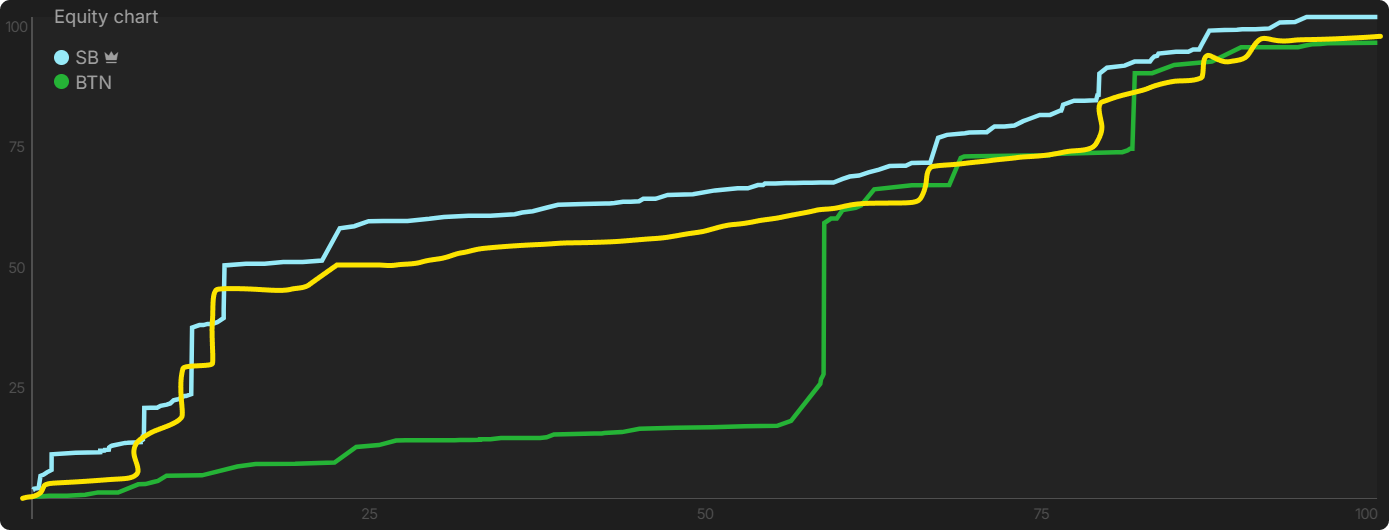
The SB has an equity advantage that is inherited from the turn. Similar to Case #1, a number of trash hands remain in the BTN’s range.
Are you starting to see through the matrix? Don’t get distracted by the woman in the red dress (i.e., the large river equity advantage). Notice that the SB does not range-bet. Let’s switch views to the Manhattan plot of the overall strategy.
Am I thinking what you’re thinking? Yes, they look very alike!
However, the equity graph looks completely different from the [0,1] game. Why does the SB employ the strategy of the [0,1] game despite having a range EQ advantage? To resolve this conflict and make sense of this, I will introduce the concepts of range-cropping and inflated EQ.
1) Cropping Villain’s Range
There are hands in the BTN’s range that have nearly 0% equity on the river. What does the BTN do with those hands? Although they bluff-raise them occasionally, folding is the most common action.
Here we have the summary of the BTN’s river strategy with their entire range when facing a 10% pot bet from the SB:
The BTN folds ~22% of their range, showing that they defend less than what MDF would suggest. There is no intention to take a stand with these zero-equity hands; they’re pretty much waiting to throw away the trash. The SB needs to design their strategy accordingly.
We do this by cropping ✂ the BTN’s range. The yellow portion of the range point to the hands that the BTN is ready to give upOne analogy could be that of a bike race. There’s a portion of the field that’s technically still in the race, but have mentally checked out. These riders are not competing anymore. They’re a few moments away from parking on the side of the street and stepping into the ‘broom wagon.’, so you disregard this part by cutting it off. What remains is the actual range that the BTN competes with. This is the relevant range that the SB must consider when constructing their strategy on the river.
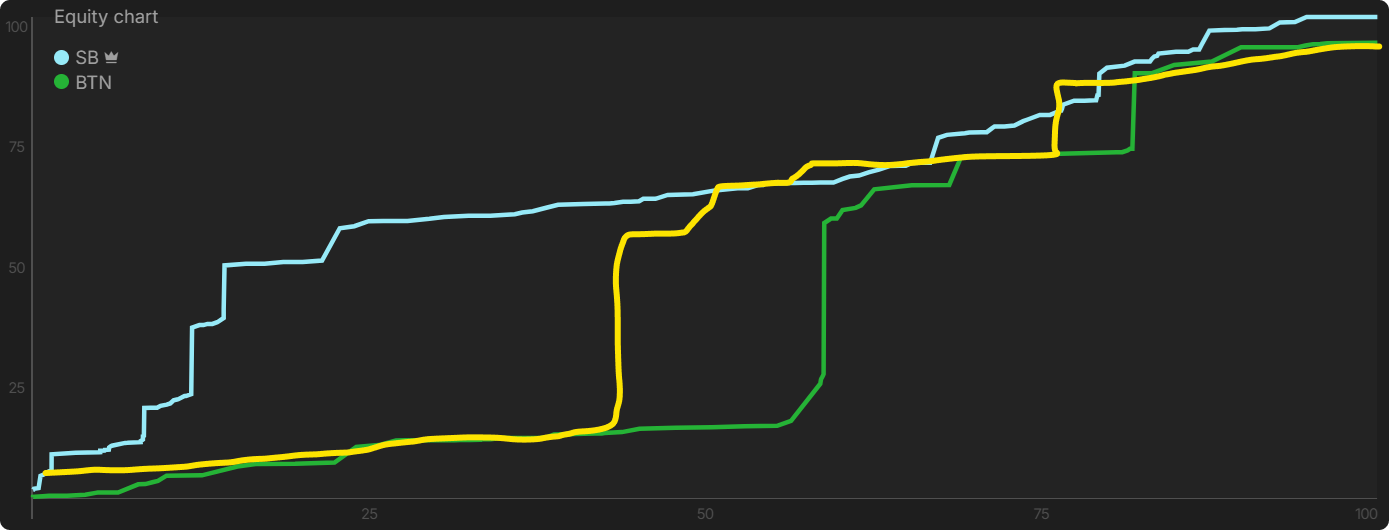
The BTN’s equity distribution has a new lower bound after the cropping. It would look something like this (see yellow line). In other words, it has been elevated a bit because it’s no longer weighed down by as much trash. So, it’s now floating a bit higher.
2) Deflating Hero’s Inflated Equity Balloon
There’s still one step left in updating the picture so that it presents the reality of the situation. We need to deflate the SB’s equity because it has been inflated. The SB’s equity distribution (see light blue line) is plotted relative to the BTN’s range. But that range has been adjusted for relevance in the previous step. The original range of the BTN includes hands that they have no interest in defending, thus inflating (i.e., superfluously elevating) the SB’s equity. But remember, the SB needs to construct their strategy against the cropped range of the BTN, which obviously is stronger than the original range. So, SB’s equity is inflated, hence the need for deflation.
The yellow line in the above graphic represents the deflated equity distribution of the SB. When you superimpose these two updated views, you will see that both ranges’ equities run much closer to each other now. Hands are distributed widely across the spectrum, like in the [0,1] game, hence the strategy is similar to that of the [0,1] game.
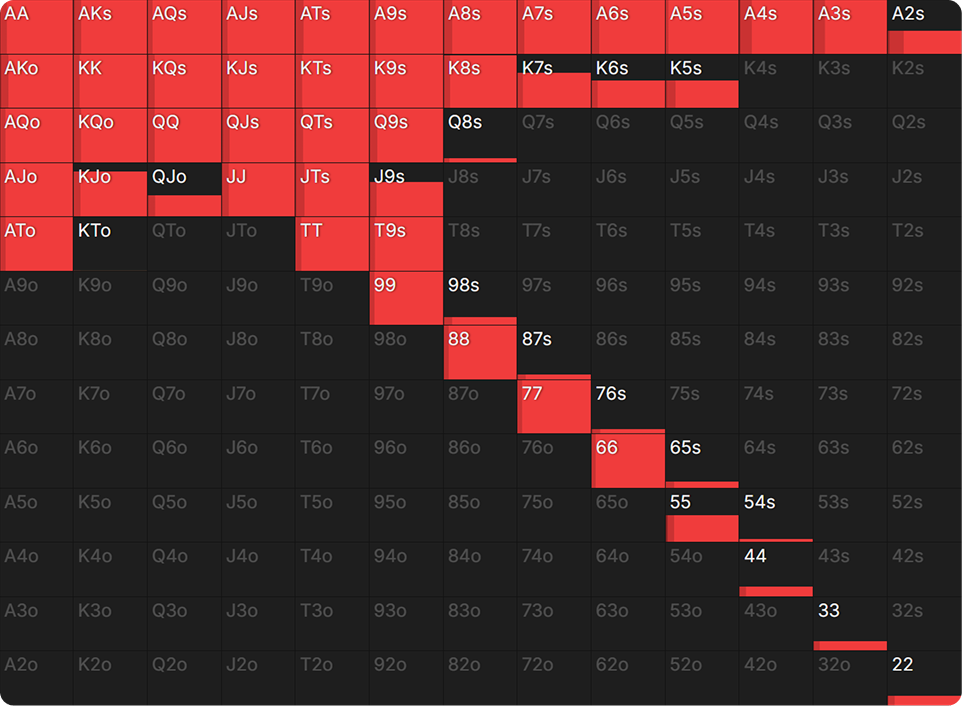
Seeing Through the (Hand) Matrix
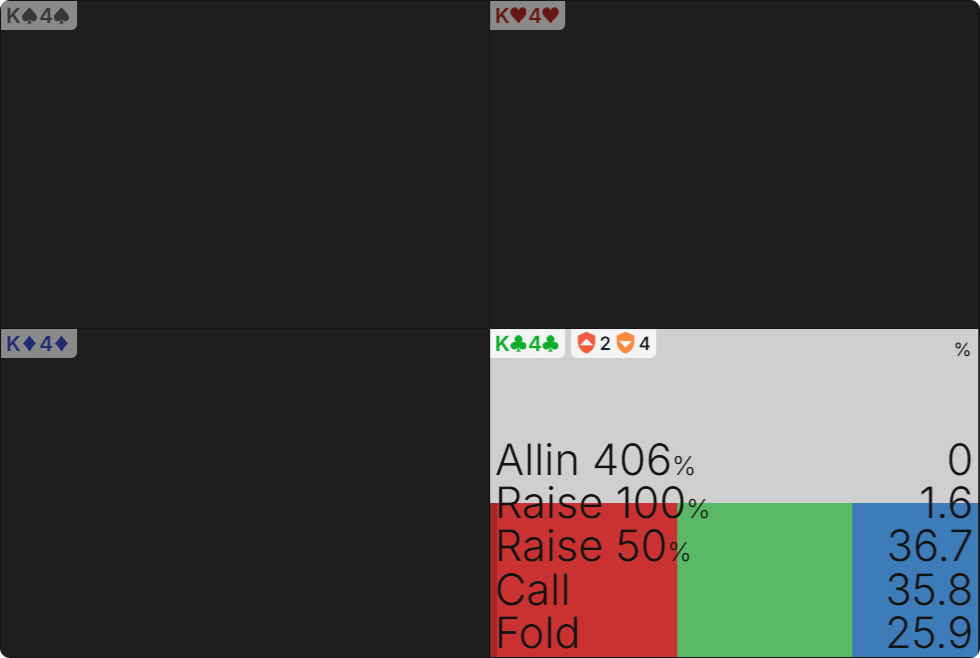
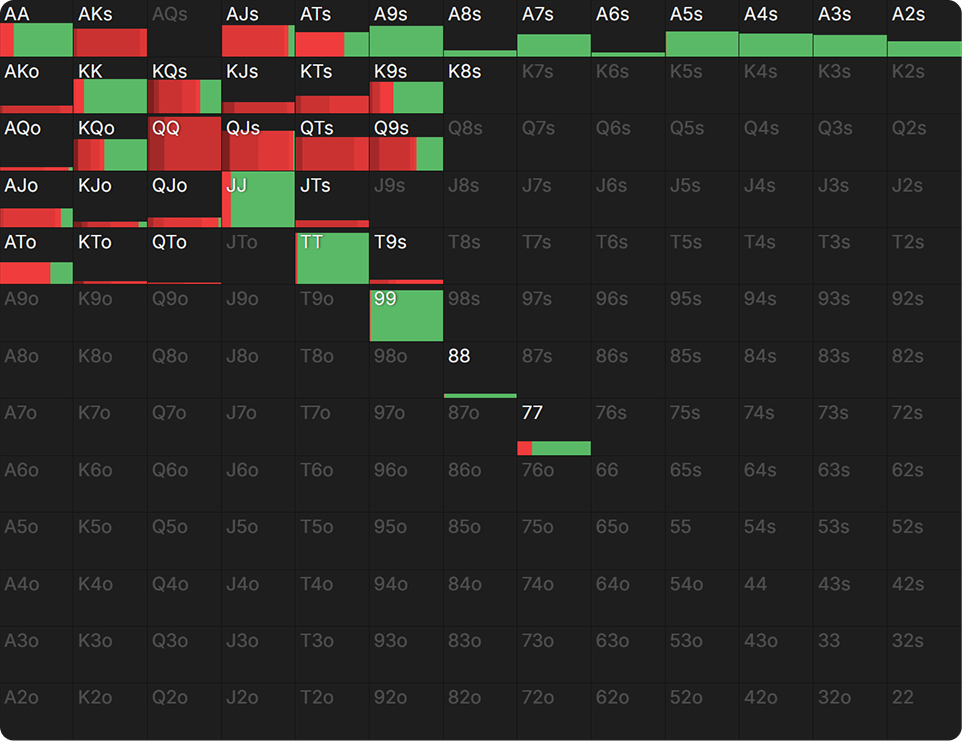
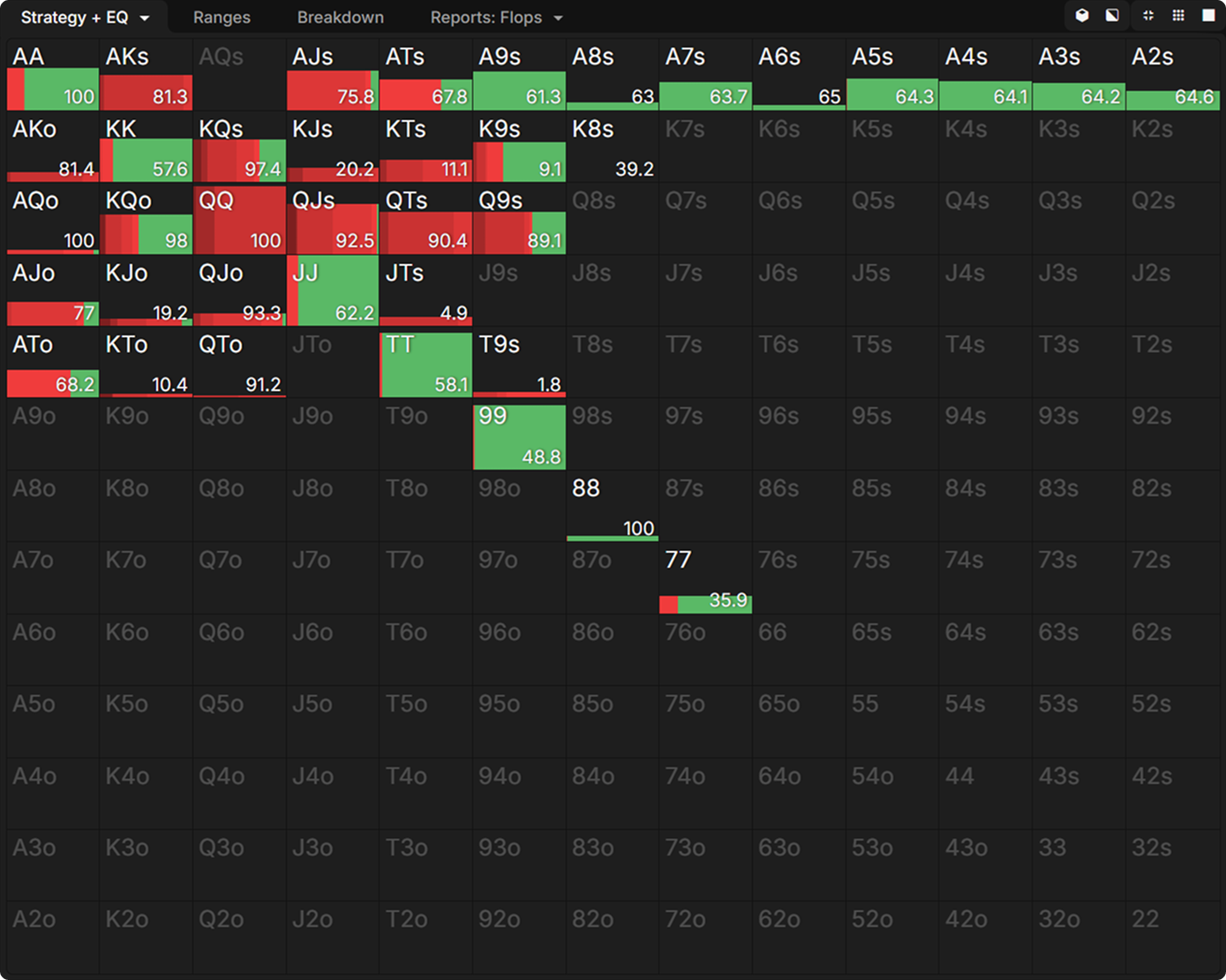
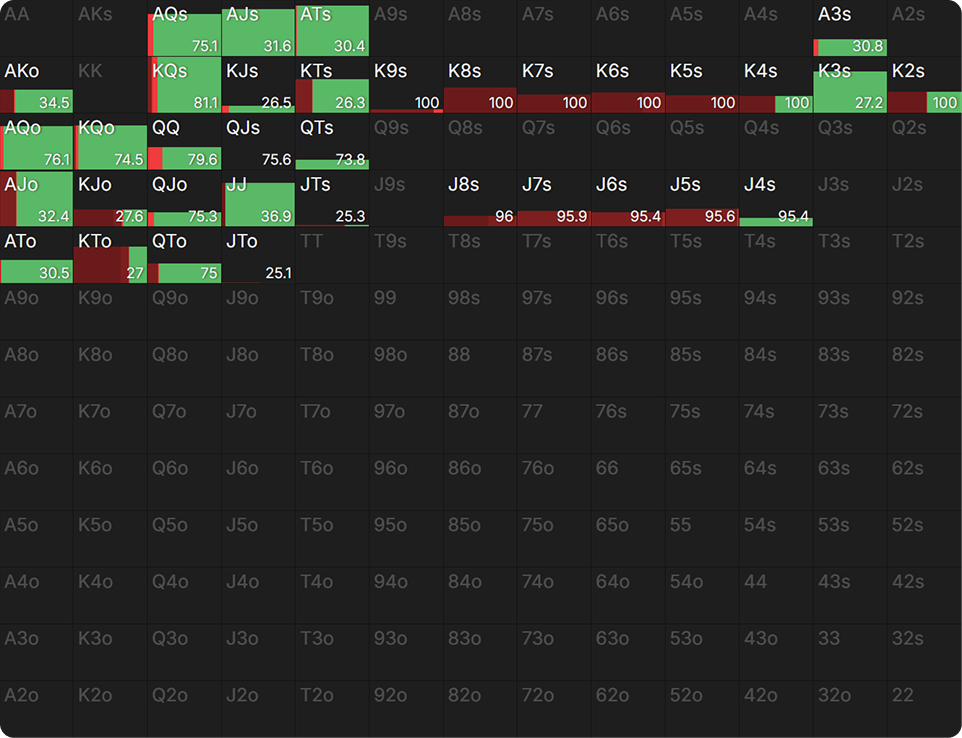
We can also observe how equity inflation affects individual hands. In the below hand matrix, the equity of each hand is displayed. Despite having over 60% equity, Ace-x with weak kickers are not betting. That is because they don’t actually have that much equity against BTN’s cropped range.
Reexamining Case #1
Alright! Our time in the lab has been fruitful. We are finally all clued in to reexamine the case study this article started with.
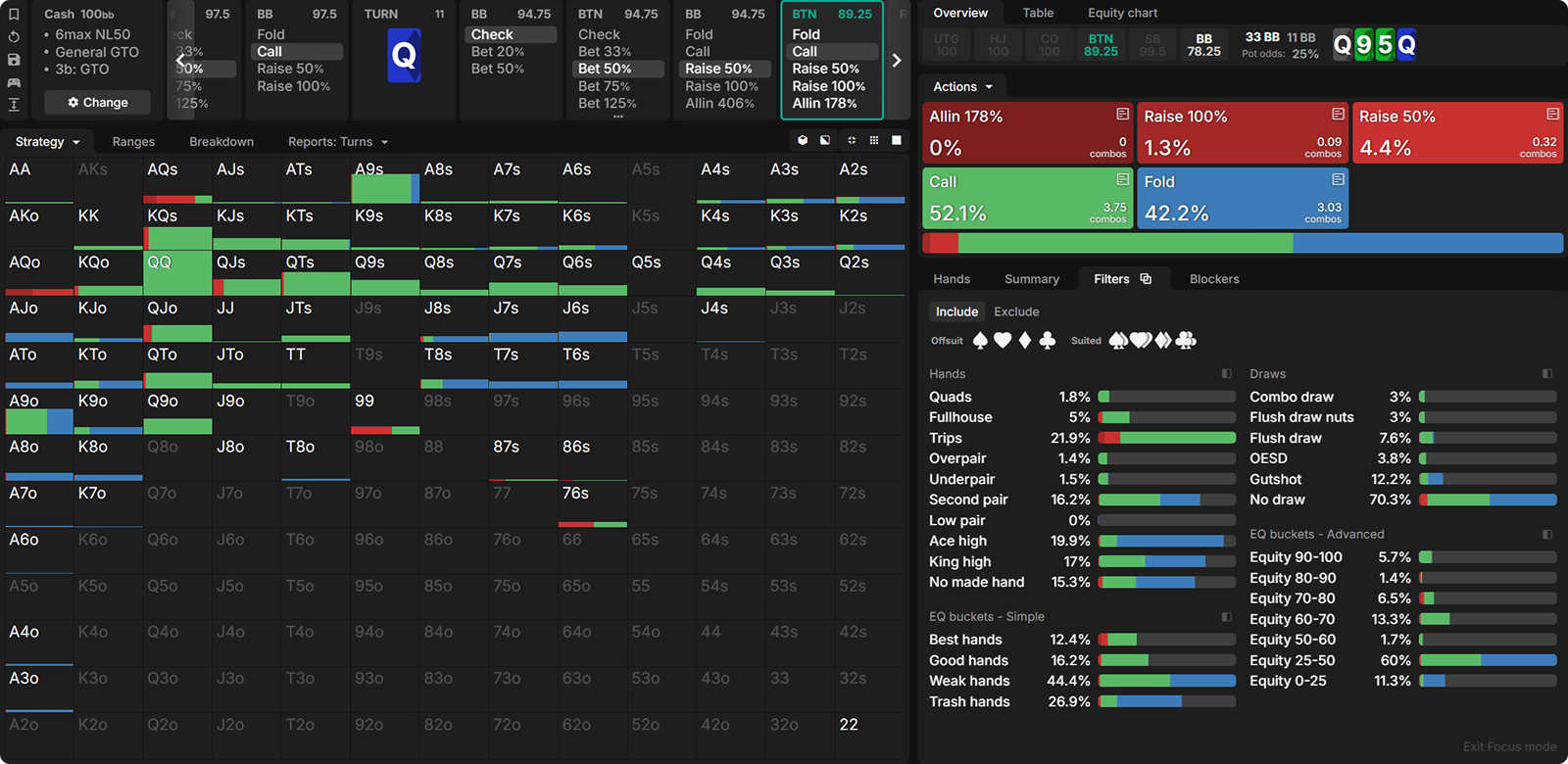
(1) Crop the BTN’s range by cutting off the near-zero equity hands, and (2) deflate the BB’s equity accordingly. The BB’s range now consists of a bunch of marginal hands, while the BTN’s range is polarized. Despite the BB having the equity advantage, the situation now looks more like the AKQ-game. If so, the BB should be inclined to check, while the BTN should make a big polarized bet.
Indeed, against the BB’s check, the BTN elects to jam with a highly polarized range. They turn many of their weak Queen-x into a bluff. (As a reminder, the board ran out Q♠9♣5♣ Q♦ 8♣ with the action going X-B50-C, X-B50-R50-C, X.)
Case Study #3: Donk-Jamming a Four-Straight River
Lastly, we will examine a spot that is slightly more complex to test the depth of our understanding.
BB check-calls twice against UTG’s (76% and 50% pot) bets. The river completes a four-straight along with the backdoor flush. Here, the BB will either check or donk-jam.
The BB has the equity advantage since the river completes many draws and they check-called twice. However, the BB’s range is revealed to be polarized after cropping the UTG’s range and deflating the BB’s equity distribution. This again resembles an AKQ-game. The difference with Case #1 is that it’s now OOP that has the polarized range. So, it’s the opposite case of Case #1, where IP was polarized. When the BB donk-jams their two pairs, they are turning them into bluffs (despite them having over 20% equity).
Conclusion
Let’s wrap things up with a brief summary of the three cases that were studied in this article.
Case #1 – The river card completed all draws. This results in the removal of all trash hands from the BB’s (turn check-raising) range. The river strategy resembled an AKQ-game where IP is polarized.
Case #2 – The equity advantage of the SB on the turn was carried over to the river. The river strategy resembled a [0,1] game.
Case #3 – The river card completed all draws, removing all trash from the BB’s range. The river strategy resembled an AKQ-game where OOP is polarized.
The main lesson to draw is that:
The equity advantage on the river by itself does not determine the river strategy.
Moreover, it could even be the total opposite, like how Cases #1 and #3 are. The concepts that I have illustrated in this article are keys to making sense of the (river) equilibrium. This theoretical understanding can then guide you through the practical task of range construction.
On a side note, carrying over the equity advantage from turn to river, such as in Case #2, seldom happens. When you have such an advantage on the turn, you would most likely range-bet the turn.
Author
Amu
Amu, armed with a master’s degree in mathematics, decided to dive into the maelstrom of cards.
With a growing stack of experiences from all his explorations and experiments, he became a trusted guide for many ambitious Japanese players. He also took on the more public-facing role of GTO Wizard Japan’s official coach and has a blog of his own: https://note.com/goole
Wizards, you don’t want to miss out on ‘Daily Dose of GTO,’ it’s the most valuable freeroll of the year!
We Are Hiring
We are looking for remarkable individuals to join us in our quest to build the next-generation poker training ecosystem. If you are passionate, dedicated, and driven to excel, we want to hear from you. Join us in redefining how poker is being studied.