Principles of GTO

The Exploitative and GTO Frameworks

Game theory, or GTO (for Game Theoretically Optimal), is best understood not as a rigid set of rules to be accepted or rejected but rather as a framework for thinking about poker, predicting your opponent’s actions, and improving your own decision making. Its objective is to avoid strong assumptions about the opponent’s mistakes, and instead build strategies that will be robust no matter how your opponents play. This makes it especially useful when playing against tough opponents but also against unfamiliar opponents whose mistakes you are not comfortable predicting.

Game theory, or GTO (for Game Theoretically Optimal), is best understood not as a rigid set of rules to be accepted or rejected but rather as a framework for thinking about poker.

Exploitative thinking is a different way of approaching these same problems. An exploitative approach tries to predict specific mistakes an opponent will make and craft a strategy that takes maximum advantage of those mistakes. This approach works best against weaker players whose tendencies are well-known to you.

In poker, these frameworks are not mutually exclusive. In fact, game theory can help you craft more profitable exploits. You may know, for example, that an opponent calls too many weak hands pre-flop but not have a clear idea how they will play all those bad hands after the flop. Game theory can help you profit from the mistake you’ve identified without opening yourself up to exploits no matter how your opponent plays their weak hands after the flop.

Why is Game Theory Useful?

Game theory is a tool for making decisions under conditions of uncertainty. In the absence of actionable information about your opponents’ intentions, it assumes they will play as well as possible, rationally pursuing their profit incentives to the best of their ability. While no human opponent will ever play perfectly, it is what most are striving for, so it’s a useful assumption when you don’t have other information to guide you.

The first step to understanding game theory is learning to think outside of an exploitative framework. This can be challenging for veteran players, because you may not realize how many assumptions are baked into the strategies you’ve learned or developed over time.

In many cases, these assumptions are warranted, and acting on them will yield better results than game theory alone. However, it’s important to recognize that they *are* assumptions so that you don’t rely on them in cases where they are not applicable.

Game Theory in Action

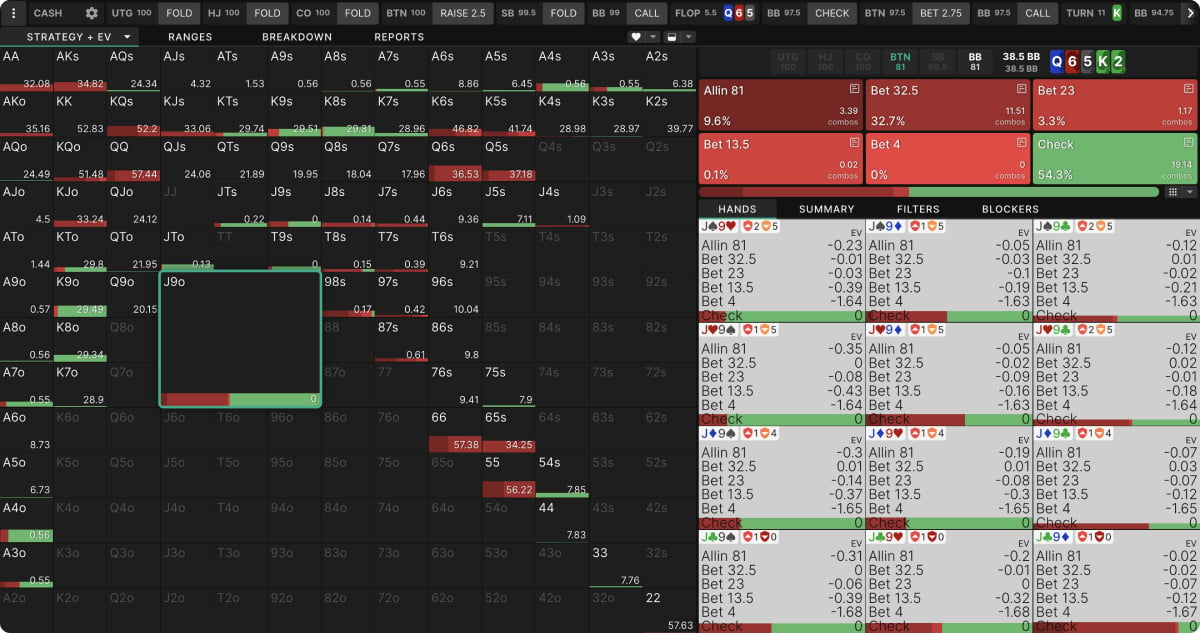
Suppose, in a cash game with 100BB effective stacks, you open J♥ 9♦ on the BTN and are called by BB. You continuation bet a Q♦ 6♥ 5♠ flop and follow it up with a big bet on a K♠ turn. Your opponent calls again, and the river is the 2♣.

Should you bluff or give up? 🤔💭

You might have an easy answer to this question if BB were one of your regular opponents. Karim never pays off big bets, so against him it’s an easy bluff. Linda hates the idea of being bluffed and loves seeing your cards, so you won’t try to bluff her.

If you didn’t know your opponent, you might rely on a simple heuristic such as, “If they were going to fold, they would have folded the turn” or “If they were strong enough to call, they would have raised the turn.”

These are all exploitative decision-making processes. They rely on guessing your opponent’s intentions and playing accordingly. If you guess correctly, you come out ahead. But if you guess wrong–if Karim is fed up with your bluffing or Linda is about to quit and doesn’t want to risk a big loss–then your opponents exploit you, even if they don’t realize it.

The unexploitable or game theoretic approach is to avoid giving your opponents easy opportunities to exploit you. Instead of trying to predict what they will do, it focuses on making your own play unpredictable so that there is no single best play for your opponent.

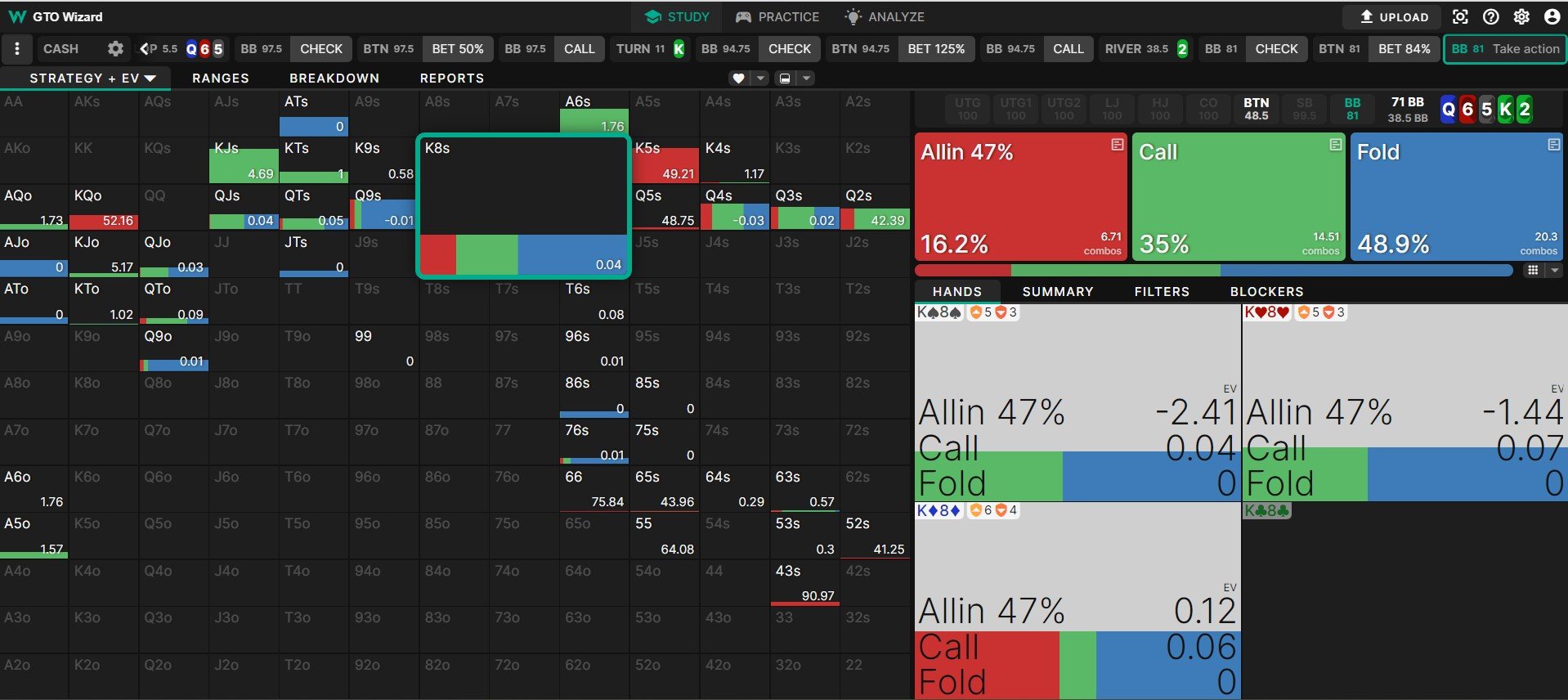
Unpredictable does not mean random. If you have 43 last to act on a Q♦ 6♥ 5♠ K♣ 2♣ board, you should bet. Checking the nuts would certainly be unpredictable, but it would not be profitable.

Unpredictable does not mean random.

Likewise, if you have K8, you should check. It’s too strong to bluff but not strong enough to bet for value. You don’t need to be unpredictable with this hand; just check and take your equity at showdown.

Your opponent may be able to predict that you will always bet your strong hands, always check your medium hands, and sometimes bet carefully chosen bluffs, but this information does not give them obvious best plays. When you bet, they do not know which type of hand you have this time. Thus, when they hold hands that will beat your bluffs but lose to your value bets, there is no way for them to outplay you. Your strategy offers them no obviously correct best play.

Here is the GTO Wizard solution for the BTN in this scenario:

Do you see how some hands clearly prefer betting or checking, but others, like your J♥9♦, sometimes bet and sometimes check? This is a result of making no assumptions about your opponent. Unlike with K8, there is no “right” play with J9. The best you can do is bluff at a frequency which, combined with all the other hands you would also bet in this situation, gives your opponent no good option with their mediocre bluff-catchers.

Here is the opponent’s response to an 84% pot bet, like the one GTO Wizard advises sometimes making with J9. Notice how even some of BB’s top pair, such as K8, has no good option when faced with this bet. Calling, folding, and raising are all equally undesirable.

In chess, there is a concept called “forking”. If you threaten just one of your opponent’s pieces, that does not give them a difficult decision, as they can simply move it to safety. When you set up a fork, you maneuver into a spot where you threaten multiple pieces at once, leaving your opponent no appealing option. They can move one piece to safety, but they will lose the other.

This river bet accomplishes the same sort of thing. If your opponent folds K8, they risk losing to your bluffs. If they call, they risk paying off your value bets. You cannot force your opponent to take any particular action, but the central goal of unexploitable poker is to play in a way that makes your opponents’ decisions difficult by denying them appealing options.

The central goal of unexploitable poker is to play in a way that makes your opponents’ decisions difficult by denying them appealing options.

Indifference

The mixed strategies in the GTO Wizard charts above represent difficult decisions. With the right strategy, you can deny your opponent especially profitable actions with these hands. When they have good hands, they will make money no matter what you do. But with smart play, you can limit how much they win.

Unexploitable play mixes between two or more options only when these options have the same EV. If no option is better or worse than another, a player is indifferent between them.

The goal of unexploitable strategies is to maximize EV. Indifference is the means by which you accomplish that goal. When you do not assume your opponent will make any specific mistake, the best you can do is deny them opportunities to make especially good plays. Learn more about indifference in this article.

The goal of unexploitable strategies is to maximize EV. Indifference is the means by which you accomplish that goal.

Mixed vs Fixed Strategies

You cannot make your opponents indifferent with every hand at every decision point. Sometimes there will be a best play, and when there is, game theory assumes your opponent will find it. These best plays appear on a strategy chart as a fixed strategy, an action a player should take every time. Remember: unpredictable does not mean random ☝ ‼

Mixed strategies “mix up” your play by sometimes taking one action with a hand and other times taking another. It costs you nothing to play these hands deceptively because you didn’t have a preference anyway. In the absence of any insight into your opponent’s strategy, you expect both (or all three, or all four, or all five) to have the same EV.

Frequency Mistakes

A mixed strategy does not imply the choice is arbitrary. Rather, the correct play depends heavily on your opponent’s strategy.

Only if your opponent plays a perfectly unexploitable strategy are the EVs of all choices in a mixed strategy the same. If you can predict even small deviations from your opponent, one option will have a higher EV and you should choose it consistently.

In our example above, the BB’s unexploitable strategy requires folding 48.9% of hands to this river bet. If they instead fold 49% of hands, bluffing with J9 will be strictly better than checking. It will not be much better, but nevertheless, you would increase your EV by bluffing every time.

By doing so, you would deviate from your own unexploitable, GTO strategy. You would be operating within the exploitative framework, making assumptions about your opponent’s mistakes. If those assumptions are correct, you would come out ahead. If they are wrong, you’d be worse off than if you stuck with the unexploitable bluffing frequency.

This mistake also loses money to players who simply call too often by habit. These players profit from your over-bluffing mistake without even knowing you are making a mistake. If you always threw rock in a game of Rock, Paper, Scissors, you would lose to any player who knew your strategy but also to any player who simply loved throwing paper as much as you loved throwing rock.

Pure Mistakes

A pure mistake would entail betting a hand that is not a good candidate for betting (or checking a hand that is not a good candidate for checking). In the Q♦ 6♥ 5♠ K♣ 2♣ example, K8 is too strong to bluff but not strong enough to bet for value. Betting it would not give your opponent difficult decisions. They would simply fold most worse hands and call all better hands.

Checking KK would also not give the opponent difficult decisions. It would give them a cheap showdown with many hands that would face a tough choice about whether to fold and risk a bluff or call and risk losing to strong hands like this one.

Unlike a frequency mistake, a pure mistake is not especially sensitive to your opponent’s strategy. These mistakes lose money even to opponents who do not do anything exploitable themselves. When you check KK, you miss out on bets your opponent would have called. When you bet K8, you lose money unnecessarily to better hands when you could have had a free showdown.

Even pure mistakes are mistakes only within a game theory framework. These “mistakes” could theoretically be profitable parts of an exploitative strategy if your opponent made the right kind of mistake themselves. Against a massive calling station who would call river bets with many bad hands, for instance, betting K8 would be profitable even though GTO Wizard shows it as a pure check.

Game theory does not require you to check this hand. Rather, it tells you that checking should be your default play unless you have a good exploitative reason to do otherwise.

A mixed strategy tells you you have a choice; there is no default play. Without any insight into your opponent’s strategy, all the mixed options are equally good. Even a hunch your opponent might deviate one way or the other gives you a preference for one option over another. Deviating from a pure strategy requires a bigger mistake on your opponent’s part to be correct.

A mixed strategy tells you you have a choice; there is no default play. Without any insight into your opponent’s strategy, all the mixed options are equally good.

Conclusion

Game theory is a tool. Like any tool, it provides value when used in the right way, in the right situations. In order to use the tool, you must understand how it works.

If you don’t understand the game theory underlying poker, you don’t really understand the game at all. At best, you’ve developed, through trial and error, strategies that work against certain types of opponents. You may be comfortable in situations you encounter commonly, but you will struggle in less familiar spots.

Using game theory does not require perfect implementation of the strategies you see on charts such as those in this article. Simply understanding the concept of indifference and learning to think in terms of giving your opponents tough decisions rather than trying to guess how they will decide will go a long way toward helping you better understand and perform in unfamiliar situations.