Quirks of Nash Equilibrium in Multiway

In the strategic world of poker, achieving a Nash Equilibrium, often referred to as Game Theory Optimal (GTO) strategy, is widely regarded as the pinnacle of unexploitable play. Its primary appeal lies in the defensive guarantee it provides in two-player settings. However, in a multiplayer scenario, the foundational promises of a Nash Equilibrium don’t hold. This article aims to explore the limitations of Nash Equilibrium in multi-player settings, using the concept of the Nash Gap as our guide.

Understanding Nash Distance and the Role of Nash Equilibrium in Two-Player and Multiplayer Games

The Nash distance for a player is defined as the maximum increase in EV the player could achieve by unilaterally deviating from their current strategy, assuming all other players keep their strategies fixed. In other words, it quantifies how much better a player could do by changing their own strategy while others do not. A Nash distance of zero indicates that the player is playing a best-response to the current strategies of their opponent(s), meaning they cannot unilaterally improve their outcome.

In a two-player zero-sum game, the concept of a Nash Equilibrium is particularly well-behaved and desirable. A Nash Equilibrium in such games ensures that each player’s strategy is optimal given the strategy of the other, and crucially, no player can be exploited. Because the game is zero-sum, one player’s gain is the other’s loss. If both players adopt equilibrium strategies, neither can improve their EV by deviating, and neither can be taken advantage of by the other. Thus, the equilibrium provides a defensive guarantee: it secures a player a minimum expected EV regardless of what the opponent does, assuming the strategy is followed. This makes Nash Equilibrium a robust and safe solution concept in two-player zero-sum settings.

However, the situation is fundamentally different in multiplayer games. When a player in such a game plays a strategy with a Nash distance of zero, they are playing a best-response to the current strategies of all other players. However, this does not imply the same kind of security or unexploitable guarantee found in the two-player zero-sum case.

The core issue is that, in multiplayer settings, multiple opponents may simultaneously change their strategies in a coordinated or adversarial way. A strategy that is optimal given the current strategies of others might become vulnerable if multiple players shift their strategies together. For instance, in a three-player game, two players could (intentionally or unintentionally) adjust their strategies in a way that exploits the third player, even if that third player is currently playing a best-response. This lack of strategic stability means that equilibrium strategies in multiplayer games do not guarantee protection against exploitation the way they do in the two-player zero-sum case.

So Why Do We Still Aim for Nash Equilibrium in Multiplayer Games?

Despite the absence of a defensive guarantee, converging to a Nash Equilibrium (or minimizing Nash distances) in multiplayer games still provides valuable insights and practical benefits. First, strategies with a low Nash distance ensure that players are playing approximately best-responses, which tends to lead to more stable and predictable gameplay in practice. In fact, under a common and often reasonable assumption in many strategic learning settings, that players are not colluding, are greedily optimizing their own outcomes, and are all aiming to minimize their own Nash distance, the system tends to converge toward a stable point, which is a Nash Equilibrium. In this sense, a Nash Equilibrium naturally happens given how individual players learn and act out of self-interest. You don’t need a central coordinator or for players to cooperate; the simple fact that each player is trying to improve their own situation is enough to collectively push the entire game to a stable point (the Nash Equilibrium), which makes Nash Equilibrium a valuable point in multiplayer dynamics. Second, equilibrium strategies can act as a baseline or starting point for more sophisticated approaches, such as opponent modelling or adaptive learning. And finally, Nash Equilibrium remains a central concept in game theory. It defines a state where no single player has an incentive to deviate, making it a natural target for learning algorithms and theoretical analysis, even if it lacks the defensive properties of the two-player zero-sum case.

Theoretical Example: Three-Player Kuhn Poker

In this section, we will take a look at three-player Kuhn poker (Solution Link). Kuhn poker is a very simplified version of poker, and perhaps you know it as the “AKQ game”. It is originally a two-player game, and its Nash equilibrium was analyzed by Harold W. Kuhn, hence the name. Fortunately, a family of Nash equilibria is also analytically known in the three-player version, though the analysis is much more complex than in the two-player version.

Now, let’s quickly review the definition of three-player Kuhn poker. The deck consists of only four cards: let’s say A, K, Q, and J. All three players receive one hole card each, and there are no community cards. There is only one betting round: all players must post an ante of 1, and they can choose whether to go all-in with their remaining stack of 1.

The known family of Nash equilibria for three-player Kuhn poker includes discretionary parameters for Player 2 and Player 3. This means that there are infinitely many equilibria, and although Player 1 has no options, Player 2 and Player 3 can change their strategy to some extent while maintaining the best EV for themselves. It is an open question whether there is another equilibrium outside this family, but our solver produced a solution within it.

An interesting phenomenon occurs here: Player 2 can choose a parameter β between 0 and 1/4 while maintaining his EV, where β roughly corresponds to Player 2’s bluffing frequency. The Nash equilibrium with β gives the following EVs to all three players:

This means that Player 2 can distribute a certain EV however he likes between Players 1 and 3, even if Player 2 doesn’t collude with any other players. In other words, Player 2 has to choose the parameter β in any case, and he will most likely select a proper value based on observations such as player skills, if he tries to maximize his EV.

It should be noted that we are discussing a simplified game designed for theoretical analysis, so the dynamics of a real-world poker game may differ. However, in theory, it would be useful to keep in mind that this kind of quirk can always occur in a game with three or more players.

Does This Happen in Real Hold’em?

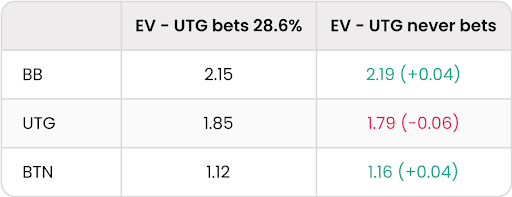
Although it’s an interesting example, this EV transfer problem doesn’t seem to be a large concern in Hold’em. In writing this article we tried to find a few realistic examples of EV transfer and came up short. It’s instructive to see how this fails to happen in real games. Here’s a common 3-way pot, where UTG raises preflop, the BTN and BB flat, and players check down to the river. At equilibrium, the UTG player bets the river 28.6% of the time when checked to. What happens if we force UTG to stop betting, while locking BTN and BB’s initial strategy in place? In 3-way Kuhn, this would transfer EV from the BB to the BTN, with no difference made to UTG’s EV. However, in this more realistic example, we see something very different:

All that happens is that UTG is giving EV away! Note that because this is a raked pot, the EV changes do not sum to 0. This is why we’re confident that aiming for a Nash Equilibrium is a robust strategy. In complex spots, playing well is the priority, and opportunities for EV transfers are impractically difficult to find.

Summary

In this article, we have explored why the unexploitable guarantee of a Nash Equilibrium in two-player settings doesn’t perfectly translate to multiway scenarios. In theory, as the 3-player Kuhn Poker example shows, it is sometimes possible for a player to transfer EV between their opponents without affecting their own EV. However, in the complex world of No-Limit Texas Hold’em, these clean opportunities for EV transfers are practically nonexistent and extremely difficult to execute. In fact, Nash Equilibriums provide a strong baseline that protects you from making costly errors and guides you towards long-term success in poker.