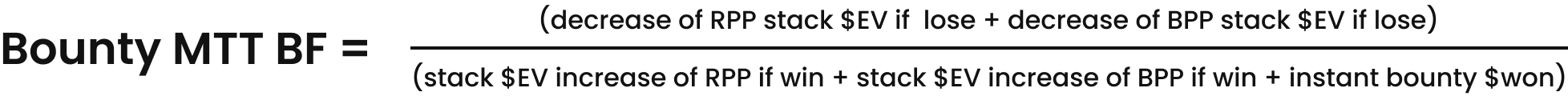The Theory of Bounty Tournaments – Part 2: ICM and Equity Drops

In part 1 of “Introduction to Bounty Theory,” we analyzed how the structures of bounty tournament prize pools form the basis for several potentially significant insights into the fundamental differences between bounty and non-bounty MTTs. In particular, we noted that the two prize pools—the bounty prize pool and the regular prize pool—have different natures:

The regular prize pool functions the same as in regular, non-bounty tournaments and can be modeled by ICM.
The bounty prize pool, however, is not distributed by placement in the tournament and so can not be modeled by ICM but largely follows the Chip EV model instead.

Building on the foundation of these observations, this article takes a deeper dive into the theoretical implications of understanding the two prize pools as operating distinctly but in concert together throughout a bounty MTT.

In particular, this article will explore how and why:

The impact of ICM on the regular prize pool competes with the $value (equity drop) of winning the bounty instantly and increasing our proportional (Chip EV) share of the bounty prize pool as a bounty MTT progresses.
The optimal strategies for winning the most from the total prize pool may differ significantly from classic tournaments because of the ways that winning a bounty impacts the potential total $value of our stack if we win an all-in pot as the covering player.

ICM and Bounty Equity Drops

At any point in a bounty MTT, players simultaneously experience a positive (ICM) risk premium in relation to the regular prize pool and a negative (bounty) equity drop—for covering players only—in relation to the bounty prize pool. Both covering and covered players also have their bubble factors impacted by their future Chip EV share of the bounty prize pool (see the bounty bubble factor formula below).

Equity drop refers to the negative risk premium pressure that the value of the bounty adds to our calculation of the bubble factor (BF)—or total risk premium—for a given spot.

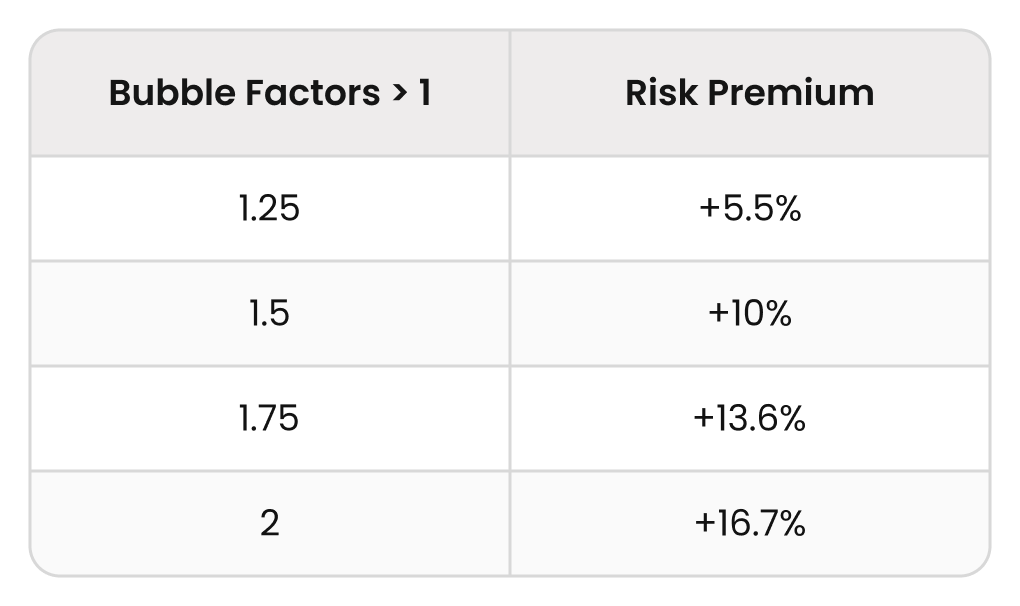
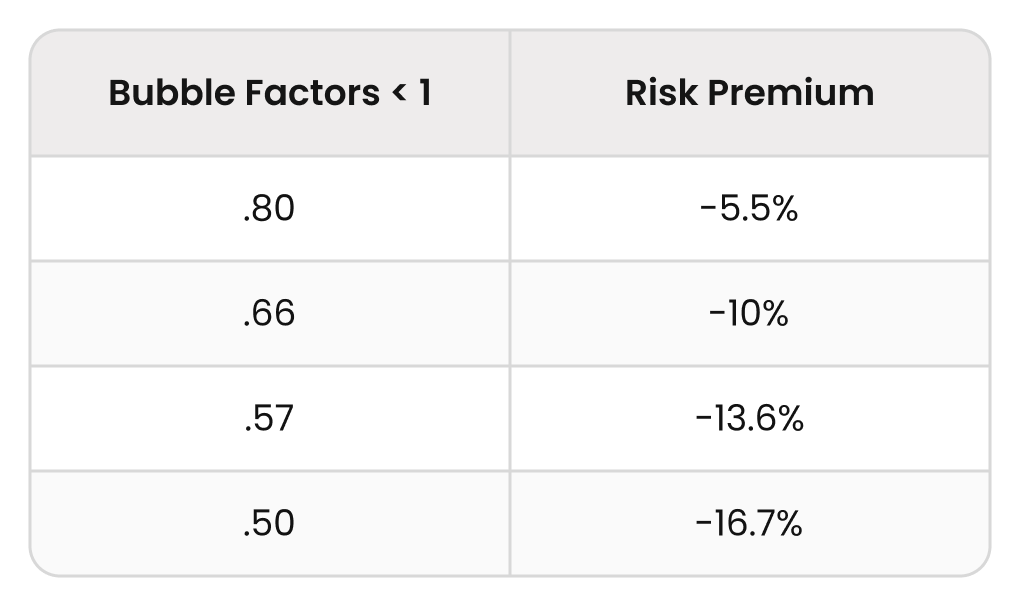
Let’s consider ICM bubble factors for each format:

In regular, non-bounty tournaments, bubble factors are always >1 and thus correlate to positive risk premiums (expressed in percentages). For example, a bubble factor of 1.5 converts to a +10% risk premium.
In bounty tournaments, however, bubble factors can be <1, which convert to negative risk premiums.

(A bubble factor of 1 = zero risk premium or Chip EV.)

This is because, when a bounty is in play, we add the $value of the instant bounty to be won to the value of our stack if we win the (all-in) pot, as well as the future EV of winning bounties later in the tournament. The below toy game example provides a demonstration of the fundamental variables that impact the calculation of bubble factors in all types of MTTs. In this theoretical example, we assume SB shoves all-in, and BB calls the first hand of a $100 regular tournament and a $50+$50 Standard Knockout (SKO) bounty tournament (no antes):

In a regular tournament, doubling up the first hand roughly doubles our stack $EV (this is rounded up; in reality, it will be slightly less than 2x because some of the tournament equity from busting a player will be distributed to all the other remaining players). Similarly, in an SKO tournament, our stack $EV for the regular prize pool also (slightly less than) doubles if we win an all-in pot in the first hand. In addition, in the SKO, our share of the bounty prize pool almost exactly doubles because the bounty prize pool is modeled by Chip EV—plus, we also immediately win $50.

The bubble factor in the regular tournament can never be <1 because the potential increase in our stack $EV when winning a pot can never be greater than the decrease in our stack $EV if we lose. The fundamental principle of ICM is that the chips we win are worth less than the chips we lose. In the early stages of the tournament, this difference is subtle and negligible, but it becomes clear in stages of the tournament that are highly pressured, such as money bubble and final table spots.

Final Table Example: ICM and Equity Drops

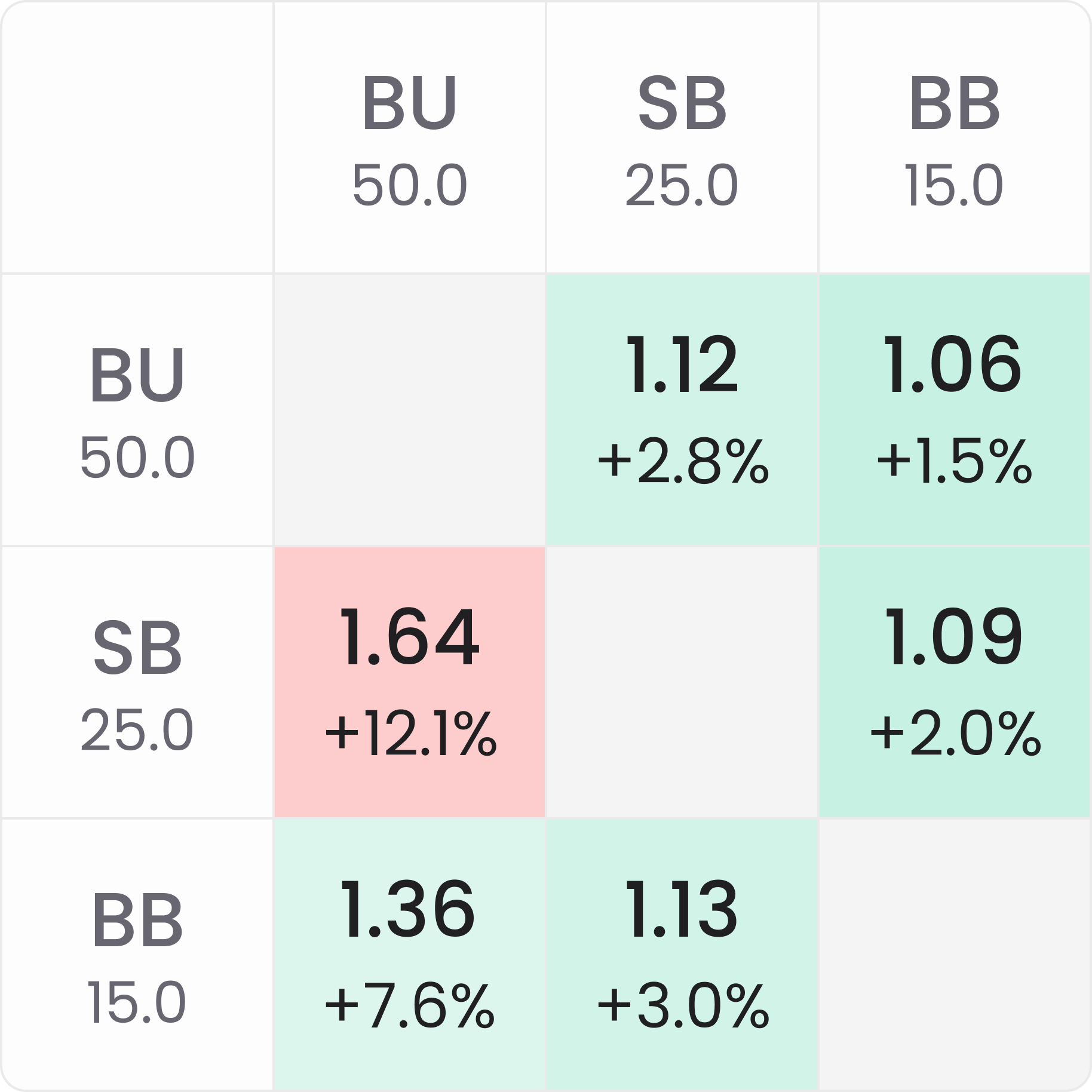
Below, we compare the bubble factors and how they are calculated in two different tournament formats with three players remaining.

The regular, non-bounty $100 tournament

The prize pool remaining = $700 with the following payouts:

$400
$200
$100

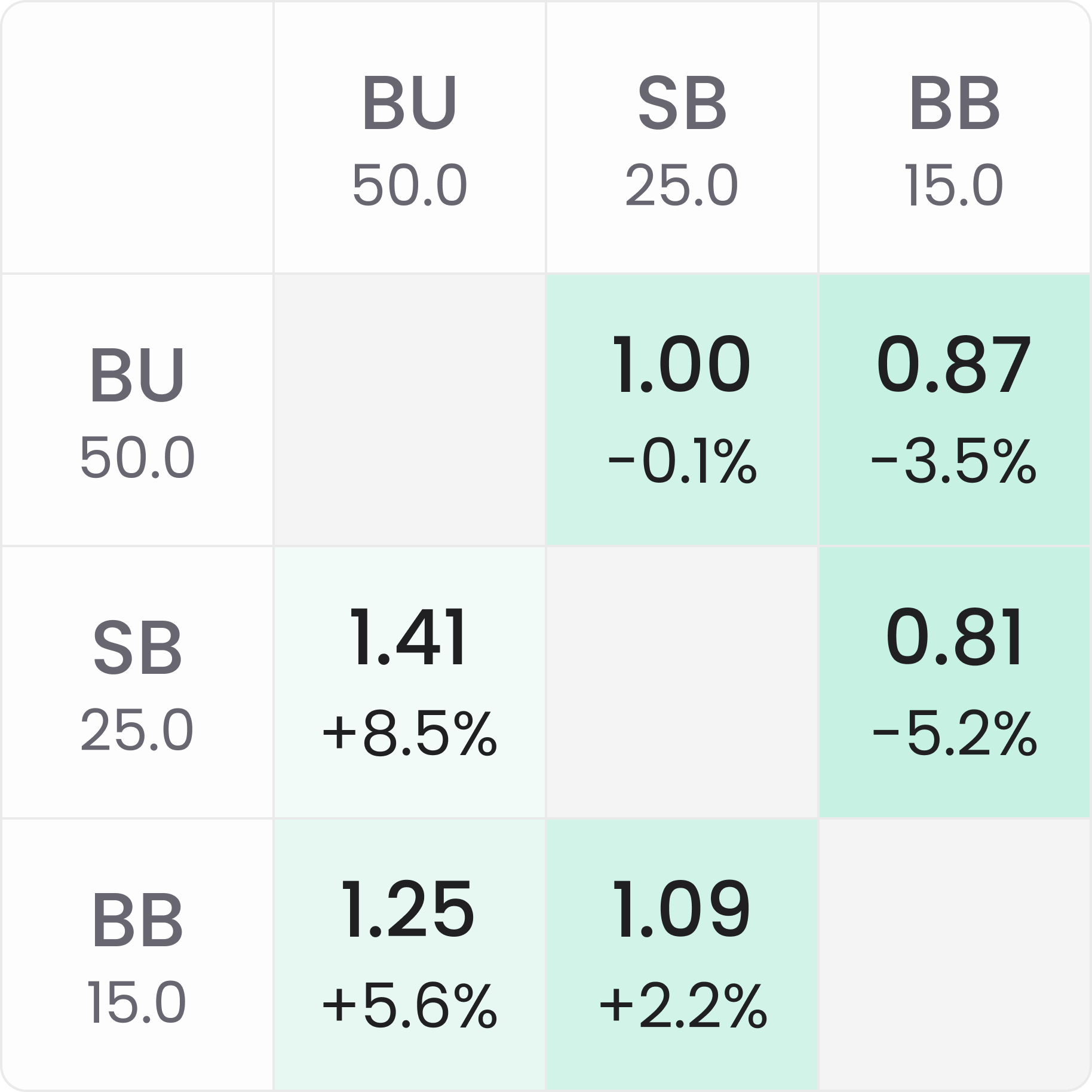
The SKO $50+$50 tournament

Same payouts for the regular prize pool
The bounty prize pool remaining = $150 ($50 bounty per elimination of each of the three remaining players)
The total prize pool remaining = $850.

Bubble factors regular, non-bounty MTT

Regular MTT 3-way ICM

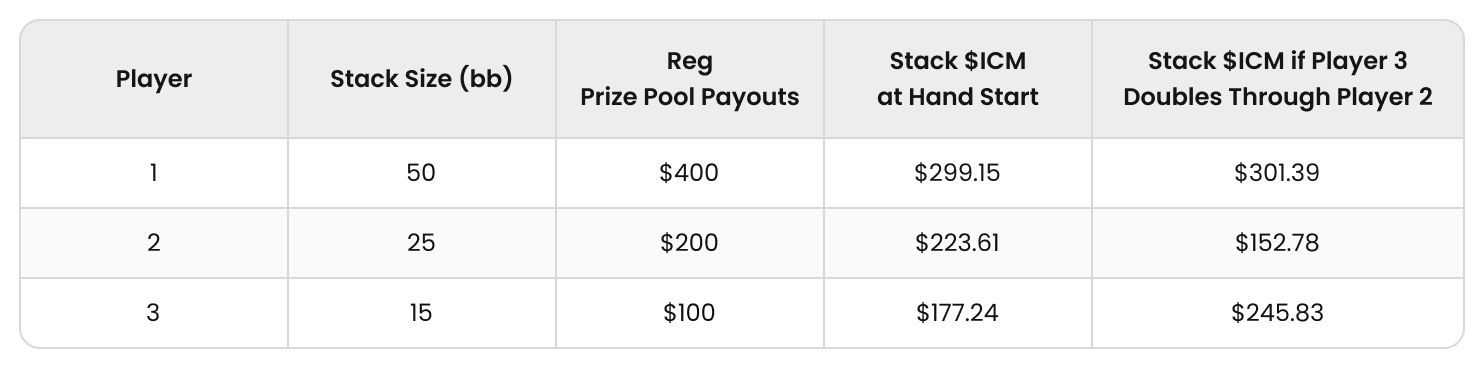
With three players remaining, the 15bb short stack has an $ICM value of ~$177 at the start of the hand ($ICM stack values here were solved by an ICM calculator). If the 15bb stack doubles through the 25bb stack, their 30bb stack will then be worth ~$246, but they will only win $100 if they lose an all-in confrontation. Thus, the 15bb short stack bubble factor vs. the 25bb middle stack is:

Regular MTT BF = decrease of stack $EV if lose / stack $EV increase if win

($177 – $100) / ($246 – $177) = $77 / $69 = 1.13 BF (approx. +3% RP)

And conversely, the 25bb middle stack bubble factor vs. the 15bb short stack is:

($223.61 – $152.78) / ($288.89 – $223.61) = $70.83 / $65.28 = 1.09 BF (+2% RP)

However, all of the bubble factors are lower if we change the above scenario to a $50-$50 SKO bounty tournament (with the same payouts for the regular prize pool), including for the covered players:

→

Bubble factors: regular, non-bounty MTT → bounty (SKO) MTT

SKO MTT 3-way ICM

In the SKO, the middle stack’s share of the Regular Prize Pool (RPP), whether they win or lose the all-in confrontation, is the same as in the non-bounty tournament. For the bounty prize pool, if the 25bb stack busts the 15bb stack, they will win an extra $50 bounty instantly, and their share of the remaining $100 Bounty Prize Pool (BPP) will increase from $41.67 to $44.44. Each player’s share of the remaining bounty prize pool is calculated by the proportion of their stack size to the total chips in play (the “proportional” or Chip EV method). So, we can calculate the bubble factor of the 25bb middle stack vs. the 15bb short stack as:

Bounty MTT BF = ($223.61 – $152.78) + ($41.67 – $16.67) / ($288.89 – $224) + ($44.44 – $41.67) + $50
= $95.83 / $118.05 = .812 (-5.2% RP)

Now that we’ve calculated the bubble factor for the mid stack vs. the short stack, we can see that the equity drop is going to be approximately -7%+2% RP ICM – (-5%) RP Bounty.

The equity drop is the difference between the total risk premium without the bounty in play and the risk premium with the bounty in play.

Bubble Factors, Total Risk Premiums, and Bounty MTTs

Bubble factors in knockout tournaments are calculated differently than in regular MTTs because of the extra value of winning a bounty when we bust a player (whether in the current or future hands). Due to the extra payout mechanism, the bubble factors of all players are also lower than in non-bounty tournaments. Though a covered player cannot access any portion of the remaining bounty prize pool in a hand where they are the shorter stack, there is still less ICM pressure on the covered stack due to the fact that a smaller % of the total prize pool is impacted by ICM vs. 100% of the prize pool in regular tournaments. In addition, there is always the potential for a covered stack to increase their stack to get (more) access (see future bounty EV).

This “future bounty EV” is expressed in bounty bubble factor calculations as the decrease and increase in stack $EV for the bounty prize pool if the player loses or wins the pot. Because all players with chips have a share in the bounty prize pool, which is modeled by Chip EV and not impacted by ICM, there are lower bubble factors in bounty tournaments overall. In fact, a covered player’s share of the bounty prize pool will exactly double if their stack size doubles.

ICM Risk Premiums and Equity Drops Are Additive

We observed in the previous article that the prize pool in a bounty MTT is split into two parts. We can also see in the bounty bubble factor formula that the decrease and increase of a player’s share of each prize pool are calculated separately and added together in the numerator and denominator of the formula.

Thus, we can extrapolate that the bubble factor in a bounty MTT can be generally expressed as:

Total Risk Premium (Bubble Factor) = Regular Prize Pool (Positive) Risk Premium + Bounty Prize Pool (Negative) Equity Drop.

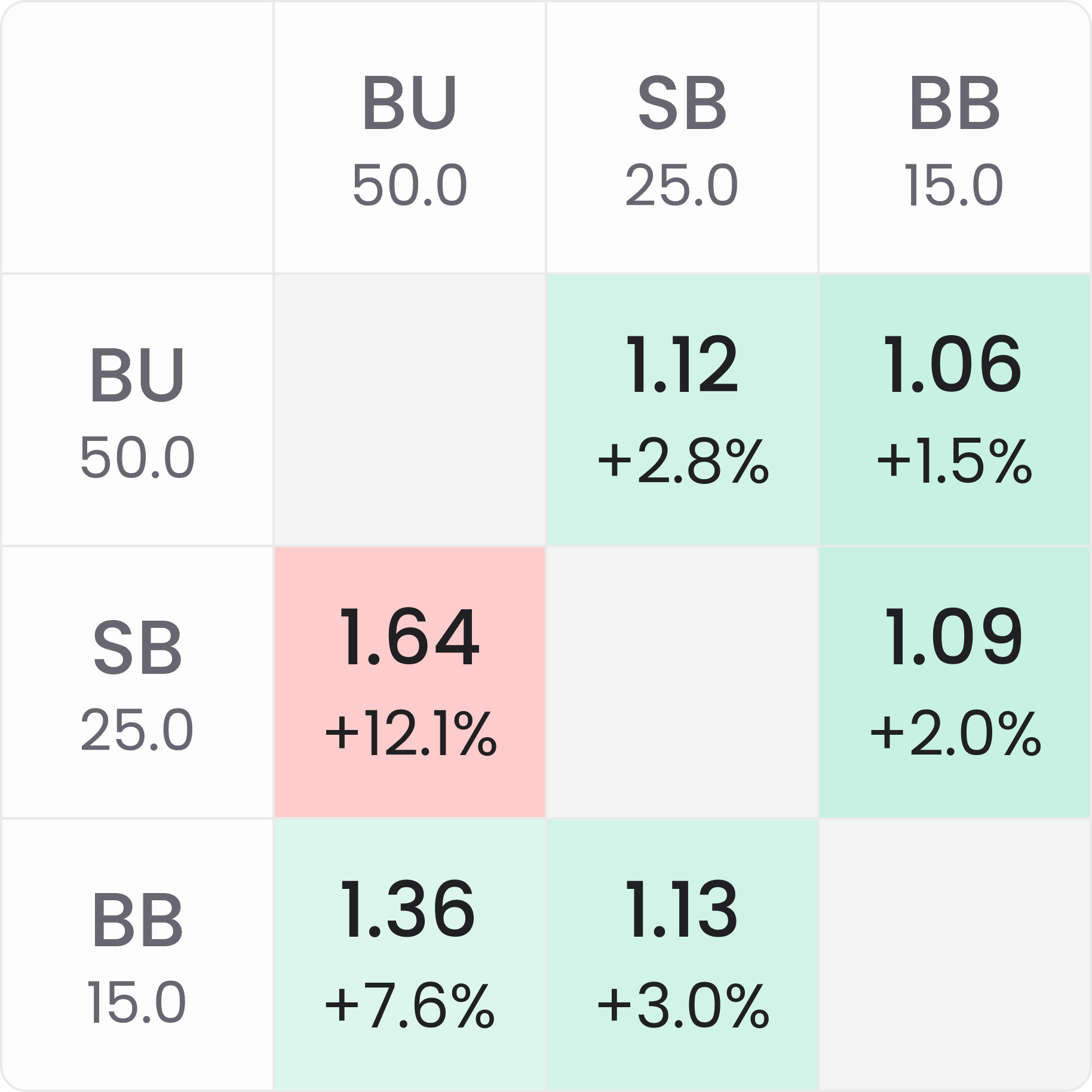
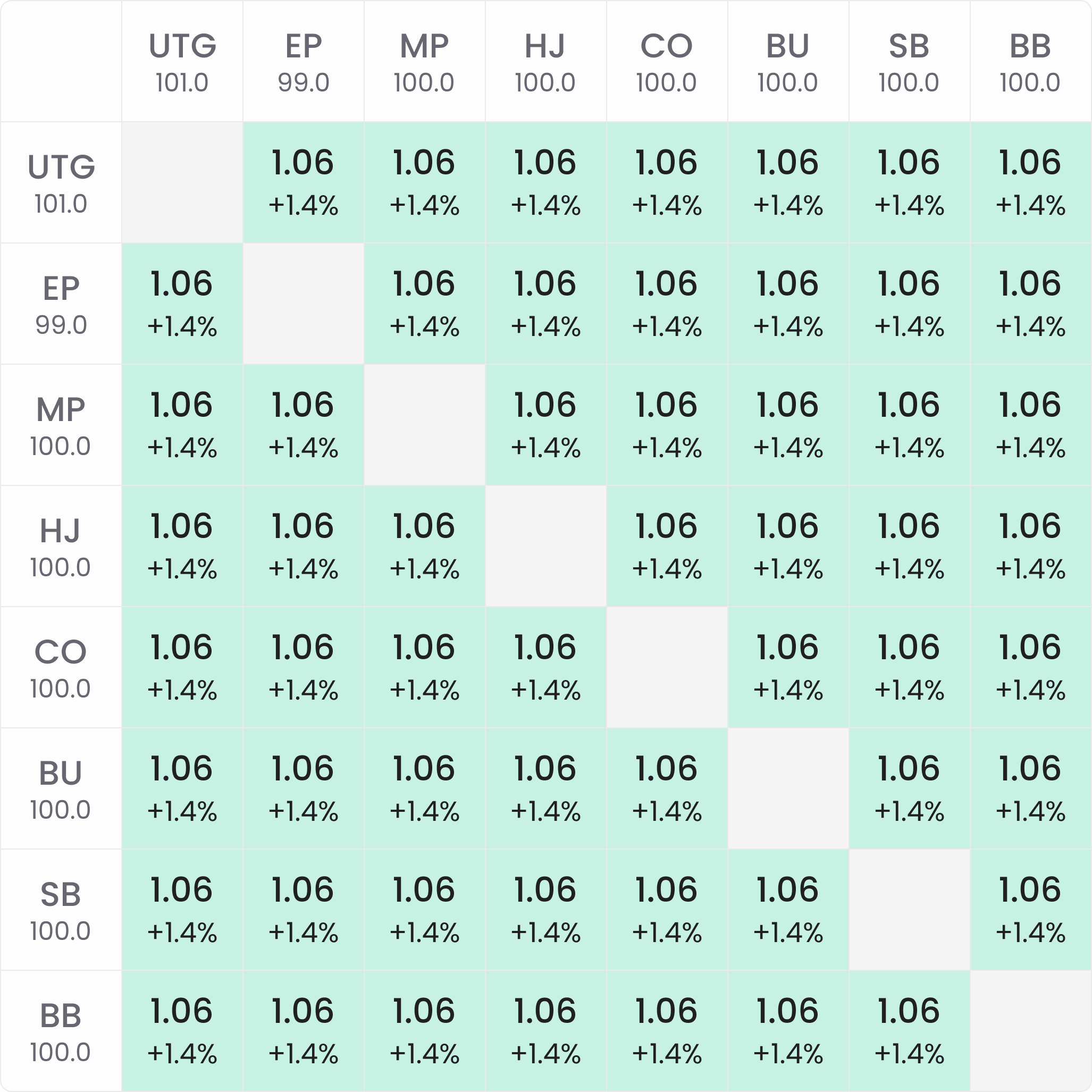
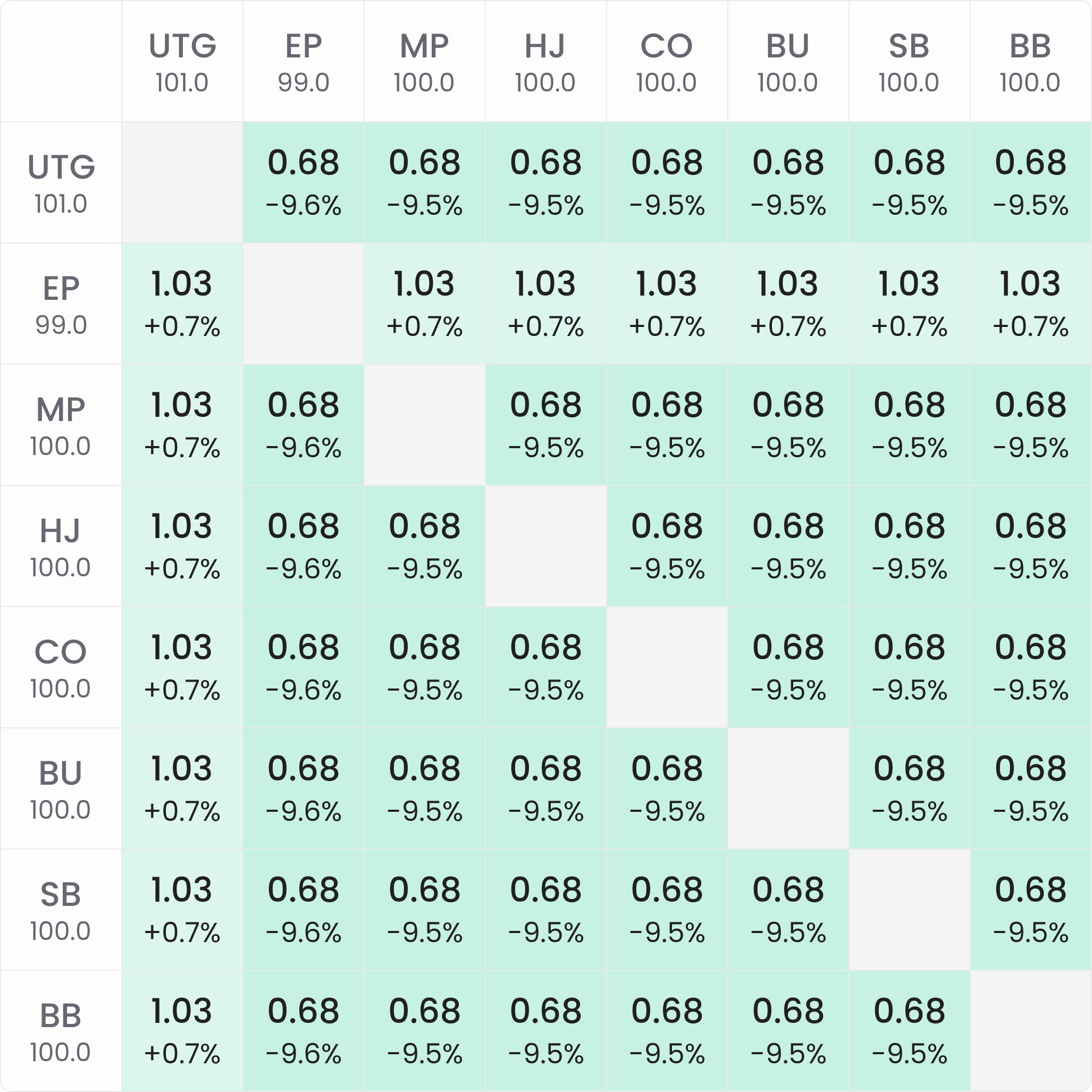
We can then use solvers to test this hypothesis. Below are the bubble factors at the start of two MTTs, both with a $100 buy-in and 1000 runners. On the left is a classic MTT, and on the right is an SKO ($50 bounty):

→

BFs & RPs (%): 1st hand Classic 1000-runner MTT → 2nd hand SKO, 1000/1000 runners remain

Looking at the above bubble factors, we can make the following observations:

In the classic MTT chart, the total risk premium for each player is +1.4% at the start of the tournament.
In the SKO chart, the total risk premium for the covered stacks is +0.7% at the start of the tournament.
In the SKO chart, the bubble factor or total risk premium for covering stacks is -9.5% to -9.6%.

In the toy game ICM model calculation earlier in this article, we determined that the equity drop for a bounty at the start of a 50% SKO ($50+$50 buy-in) was -10% (.66 bubble factor). We can also calculate this risk premium using the pot odds equation. Assuming a 10,000 chip starting stack, our share of the bounty prize pool will be worth ½ of the starting stack in a 50% SKO, or 5,000 chips (and our share of the regular prize pool is also worth 5,000 chips, for a total of 10,000). If we are in the Big Blind on the first hand of the tournament and the SB shoves all-in,

The required % equity to call = amount to call / (amount to call + opponent’s stack + bounty chip value)
= 10,000 / (10,000 + 10,000 + 5000) = .4 or 40%

With the bounty EV expressed metaphorically in chips—since we don’t actually win 5,000 more chips, we win $50 cash—we need 40% equity to call. Without the added EV of the bounty, we would need 50%, so the bounty causes an equity drop of -10%.

However, looking at the SKO bubble factor chart above, the players with a covering stack show a bubble factor of .68 (-9.5%) instead of .66 (-10%). Why?

The equity drop at the start of every 50% SKO will be -10%. However, in tournaments, there is already ICM pressure on the first hand. The covered stacks in the SKO bubble factor chart show a +.7% risk premium.

Added together, .7% + (-10%) = -9.3%; close to the -9.5% in the bubble factor chart but not exact. Why?

The .2% difference in this case is accounted for by the fact that the covering stack also wins the blinds and antes in addition to the opponent’s stack when they win the pot. It is also common to see minor deviations in the risk premium conversions due to the bubble factors being rounded to 2 decimal points.

Conclusion

In bounty tournaments, the value of the bounty of a covered player—expressed either in terms of chips added to the pot or as an equity drop percentage—is static.

There are multiple ways to establish this as an axiom. Here are two of them:

Via the pot odds calculation of the equity drop. At the start of the 50% SKO, the value of the bounty in chips is ½ of the starting stack, regardless of the covered player’s stack size.
Via the demonstration that the positive and negative risk premium pressures associated with the regular and bounty prize pools are additive, as their sum equals the total risk premium that correlates with the bubble factor.

However, the positive risk premiums associated with the regular prize pool are very sensitive to stack sizes. Thus, even though the value of each covered player’s bounty is the same for all covering players, the bubble factors or total risk premiums of all of the covering stacks will differ depending on the stack distribution of all the players at the table and in the entire tournament because of how stack distribution heavily impacts the ICM pressure from the regular prize pool.

In the next (and concluding) article in this “Introduction to Bounty Theory” series, we will explore how to implement these theories about the prize pools in bounty tournaments to determine the value of the bounty in chips and equity drops for the start of the bounty period in SKOs and PKOs.

Author

Dr. K

Dr. K (aka drkamikaze) is a passionate researcher, theorist, and teacher who has been playing MTT poker for over 20 years. They are a coach at the PokerMix, specializing in ICM and bounty tournaments.

Wizards, you don’t want to miss out on ‘Daily Dose of GTO,’ it’s the most valuable freeroll of the year!

Sharpen Your Game With Our Most Customizable GTO Trainer Ever

We Are Hiring

We are looking for remarkable individuals to join us in our quest to build the next-generation poker training ecosystem. If you are passionate, dedicated, and driven to excel, we want to hear from you. Join us in redefining how poker is being studied.

Check out the available positions here.

GTO Wizard the #1 App for Poker players

Study any spot imaginable

Practice by playing vs. GTO

Analyze your hands with 1-click

START CRUSHING NOW

JOIN DISCORD