Introducing Quantal Response Equilibrium:
The Next Evolution of GTO

The first commercial solvers appeared on the market in 2015. Since then, Nash Equilibrium has reigned supreme as the golden standard of optimal poker strategy. Today, we challenge that paradigm.

We’re excited to announce a groundbreaking new approach for solving optimal poker strategies: Quantal Response Equilibrium. QRE represents the natural evolution of optimal poker solving. Instead of assuming your opponents are perfect, we assume that mistakes can happen and produce optimal responses against them. On top of this, recent advancements to GTO Wizard AI have improved flop and turn accuracy by 25%, making our solver more precise and powerful than ever.

Here’s why QRE is the next big step in optimal poker strategy.

Jump to Section:

What Spots Does This Affect?
Why QRE is the Natural Evolution of Poker Strategy
Strategy Comparison: QRE vs Nash Equilibrium
QRE Benchmarks
Conclusion

What Spots Does This Affect?

This update applies exclusively to custom solutions solved with GTO Wizard AI. From now on, every custom spot you solve will utilize the QRE algorithm. To access custom solving, you’ll need an Elite subscription.

Want to see it in action first? All users can test QRE right now, for free, by solving this flop: Q♠T♠7♥.

All pre-solved solutions continue to use the traditional Nash Equilibrium algorithm.

Why QRE is the Natural Evolution of Poker Strategy

To explain the motivation behind QRE, we need to start by identifying one of the major shortcomings of traditional Nash Equilibrium strategies: Ghostlines.

Traditional solvers optimize strategies for spots they expect to happen, neglecting spots that “shouldn’t happen”. We call these 0% frequency spots “ghostlines”. Once a solver determines that a node/decision is irrelevant, it stops improving that spot, settling on a response just “good enough” to discourage opponents from entering that ghostline.

The problem is the lack of a defined range. If a player never takes a betting line, their range doesn’t exist—they’re representing nothing. What’s the optimal response against a non-existent range? How do you fight a ghost?

gto wizard monsters under the bed extra 1

How QRE Solves this Problem

Unlike Nash Equilibrium, which assumes perfect play, Quantal Response Equilibrium (QRE) introduces a realistic model where players occasionally make mistakes. Similar to Trembling Hand Equilibrium, QRE allows small mistakes, but with a crucial difference:

Trembling Hand Equilibrium: Random mistakes
Quantal Response Equilibrium: Mistakes occur probabilistically based on EV loss (the greater the regret, the less likely the mistake)

It should be noted that these mistakes are so infrequent that they have a negligible impact on the exploitability of the strategy. In fact, our latest engine update is 25% MORE accurate than before, as outlined in our benchmarks below. So rest assured you’re still getting the premium quality solutions you’ve come to expect from GTO Wizard AI.

In short, QRE wins more money against opponents’ mistakes without nodelocking. It gives optimal responses to ghostlines, and produces more robust strategies. This engine upgrade acts as a crucial precursor to many of the awesome updates we’re planning this year!

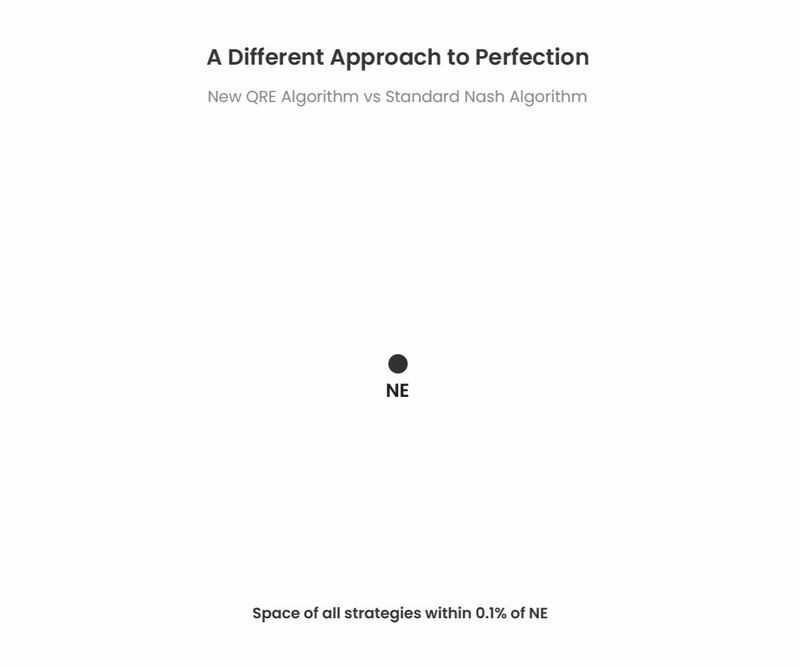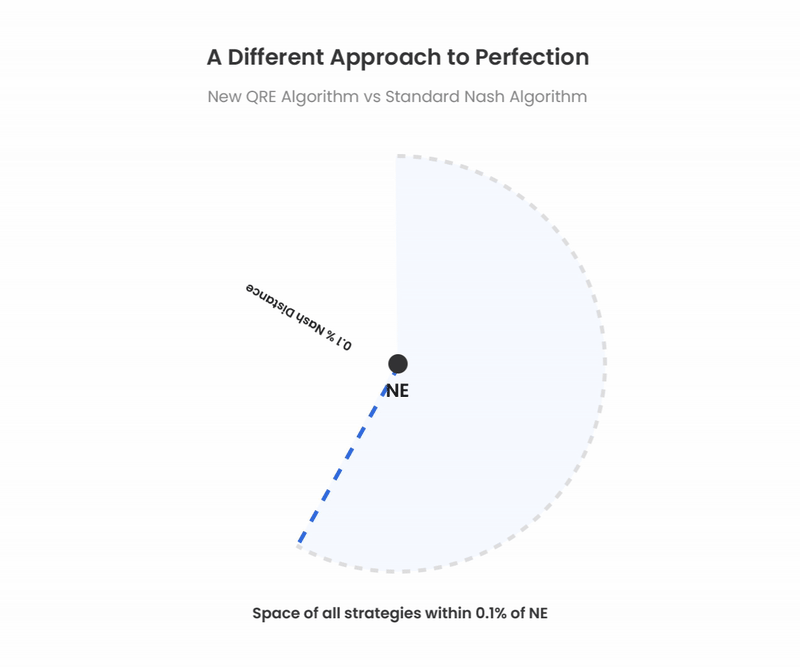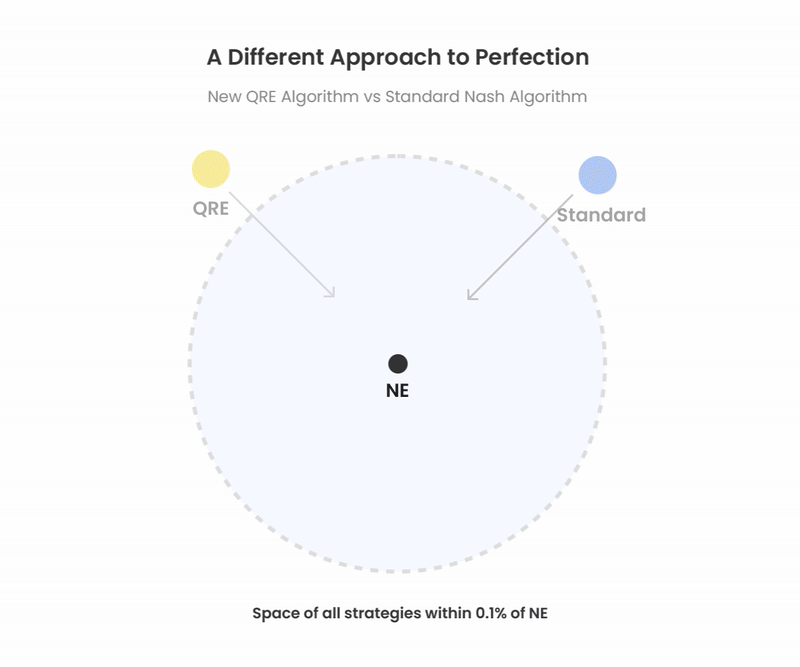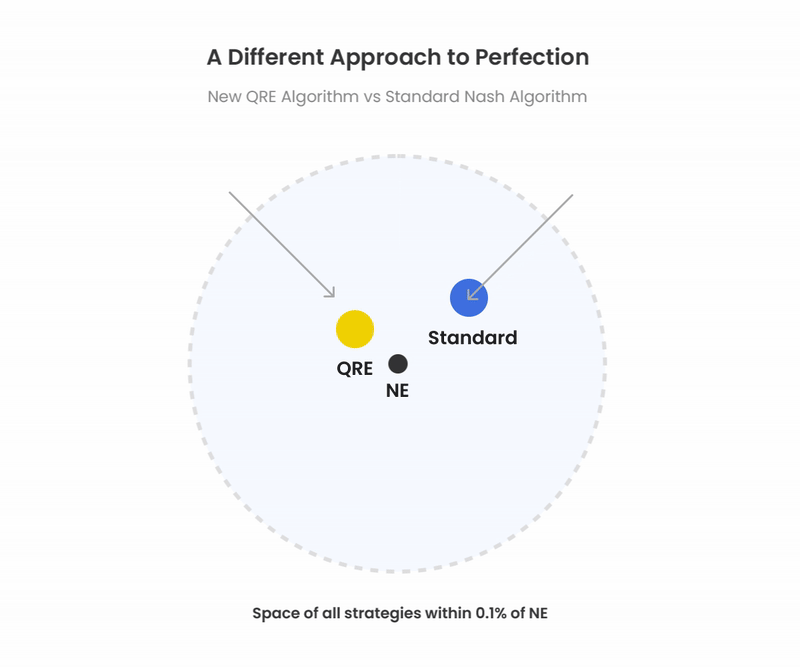
Multiple Paths to Perfection

We often speak of GTO as if it were this singular perfect strategy. In practice, GTO solutions are not solved to absolute perfection. There is always a small accuracy threshold called the “Nash Distance.” GTO Wizard AI, for example, solves to an exploitability of about 0.1% pot. This tolerance means there are many paths to optimality, and multiple strategies satisfy the Nash Distance requirements. Both QRE and standard algorithms can achieve these precise yet nearly unexploitable thresholds.

Real-World Applications of QRE

Quantal Response Equilibrium isn’t limited to poker; it has transformed understanding across fields like economics, political science, and behavioral analysis. Economists use QRE to explain phenomena like overbidding in auctions, where bidders consistently exceed their expected value. Political scientists apply it to voter behavior, explaining why people vote for underdogs despite minimal odds of affecting election outcomes. Even high-stakes game shows like The Price Is Right validate QRE, revealing systematic deviations from perfect rationality. By capturing realistic human behavior, QRE has become a critical tool for interpreting decision-making far beyond the poker table.

Strategy Comparison: QRE vs Nash Equilibrium

Example 1: Heads-Up Open Shove

Situation: HU, 50bb, no rake, no ante. The SB should typically limp or raise small. But how should the BB respond if the SB suddenly open-shoves all-in?

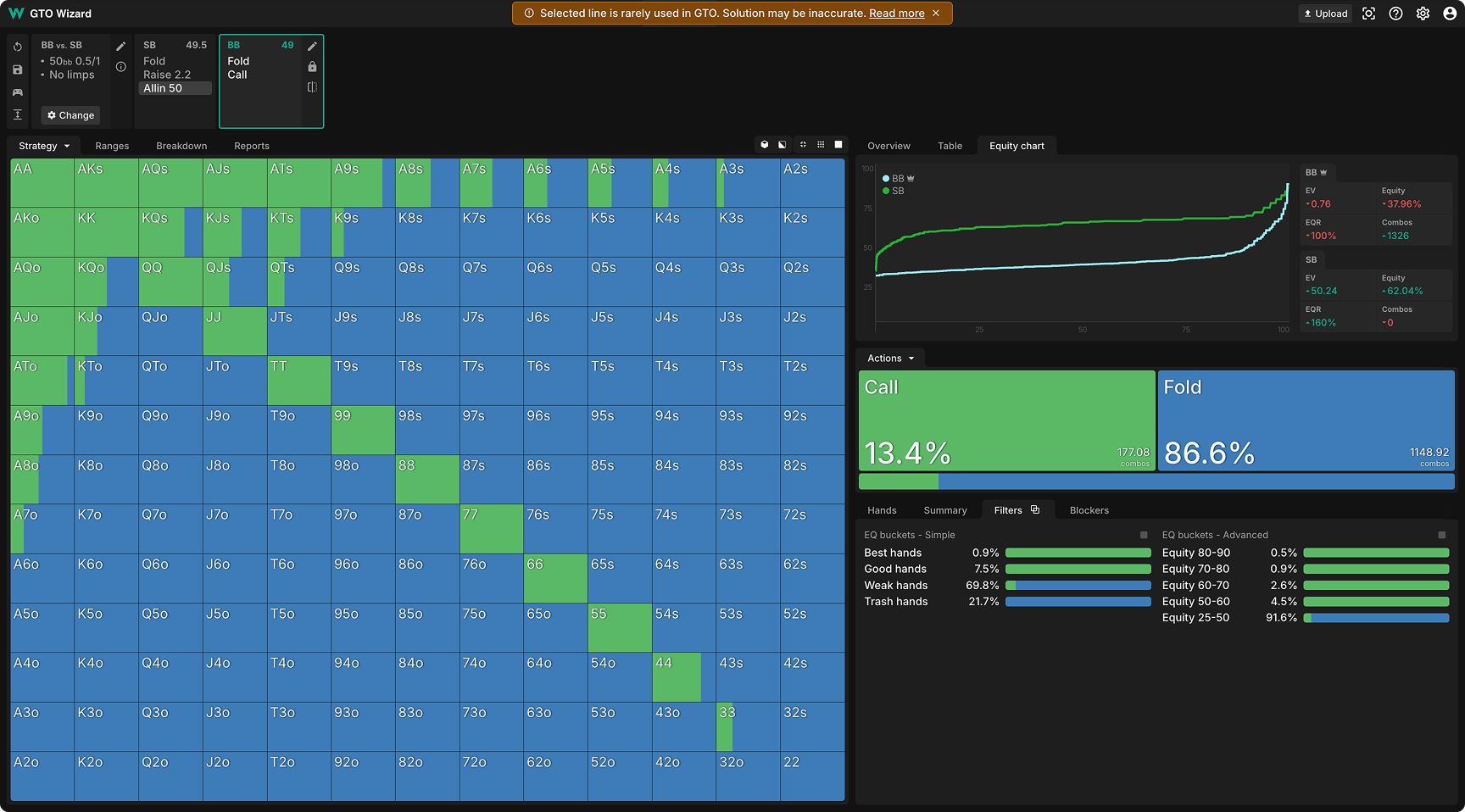
Nash Equilibrium: Look at this mish-mash of mixed strategies. Why are we folding some KQs and calling some QTs? There’s no point mixing like this when we’re going all-in. This is simply a result of the strategy not converging. The solver quickly recognized that open-shoving is a terrible strategy, and therefore, it didn’t need to think any further about the best response against it.

BB response vs SB’s open-shove (50bb): Standard Nash Equilibrium

Note the error at the top of the page, “Selected line is rarely used in GTO, solution may be inaccurate.” This was how we handled ghostlines in the past. A simple warning to tell users that this spot is questionable. Now, let’s see how QRE handles it.

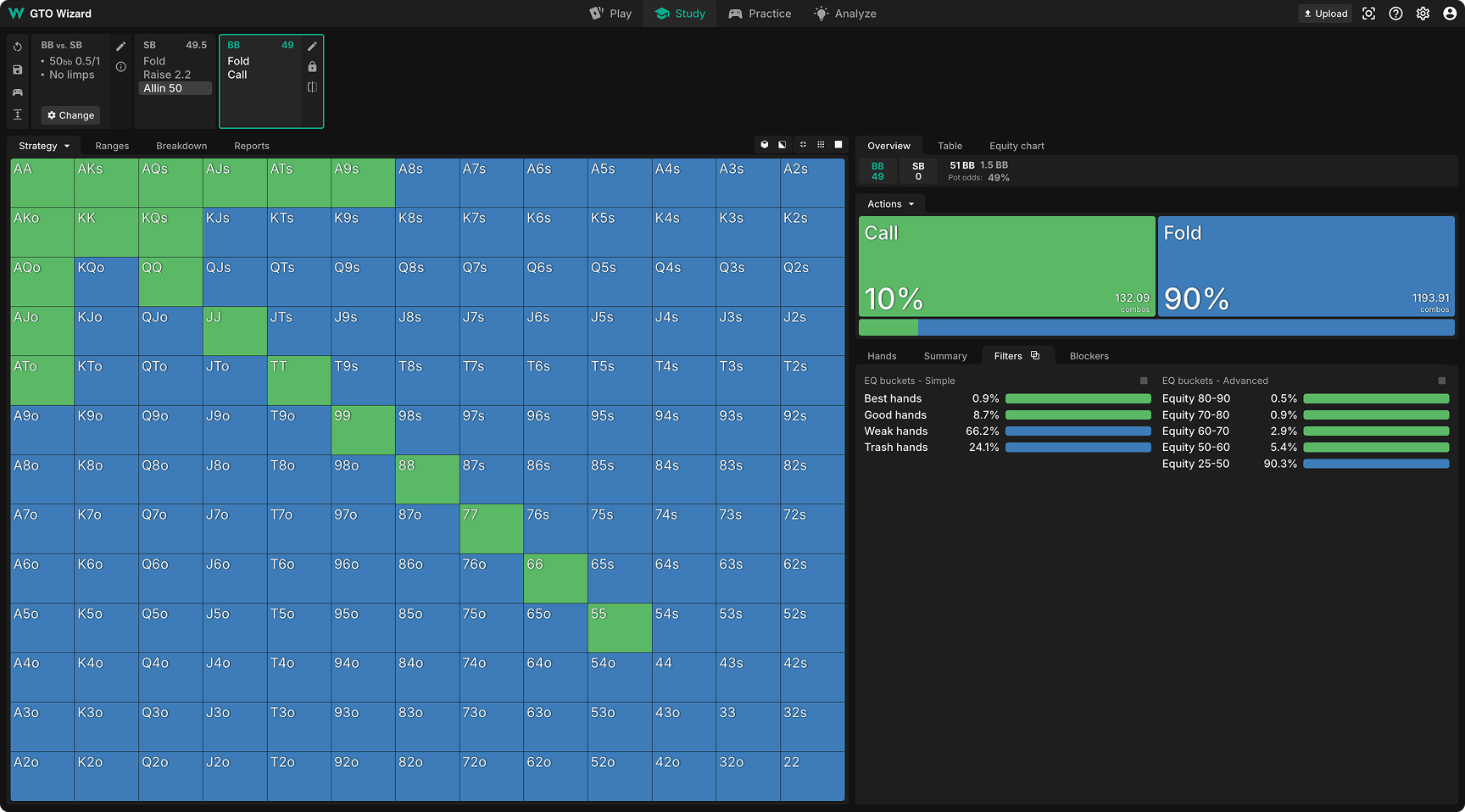
QRE: Look at these well-converged pure strategies. The solver simply calls the highest HU equity hands. Every hand that calls is +EV.

BB response vs SB’s open-shove (50bb): Quantal Response Equilibrium

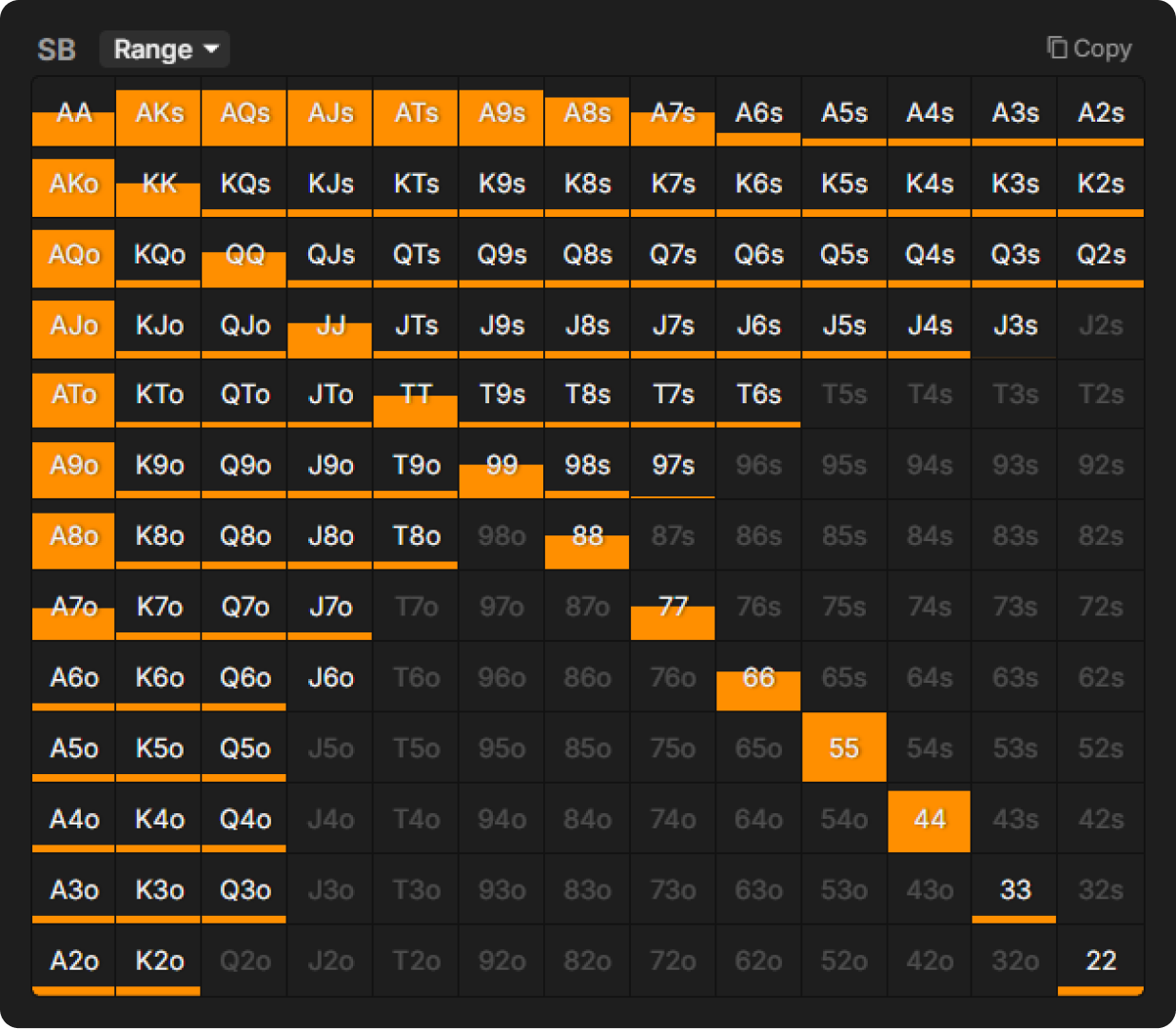
What does the shoving range look like? This range is normalized (i.e., visually rescaled max hand to 100%). The SB’s open-shoving range in QRE intuitively aligns with typical beginner mistakes: vulnerable pocket pairs, strong Ace-x hands, and some random weaker holdings mixed in:

SB open-shove (50bb) vs BB: Quantal Response Equilibrium

What about Nash? In Nash Equilibrium, the SB has no open-shove range. Thus, the BB faces no defined range, explaining why the Nash response is poorly optimized.

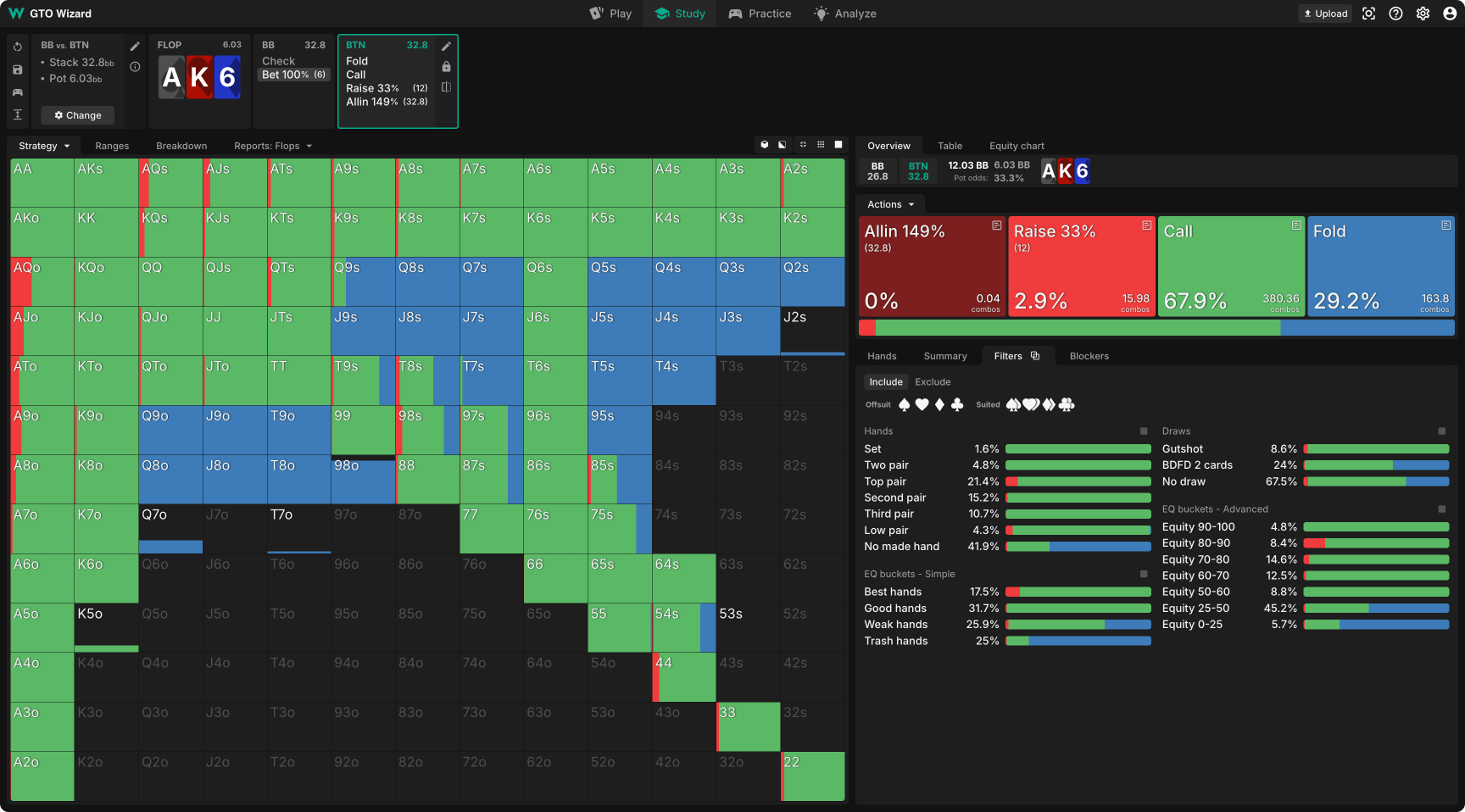
Example 2: Facing a Flop Donk – MTT

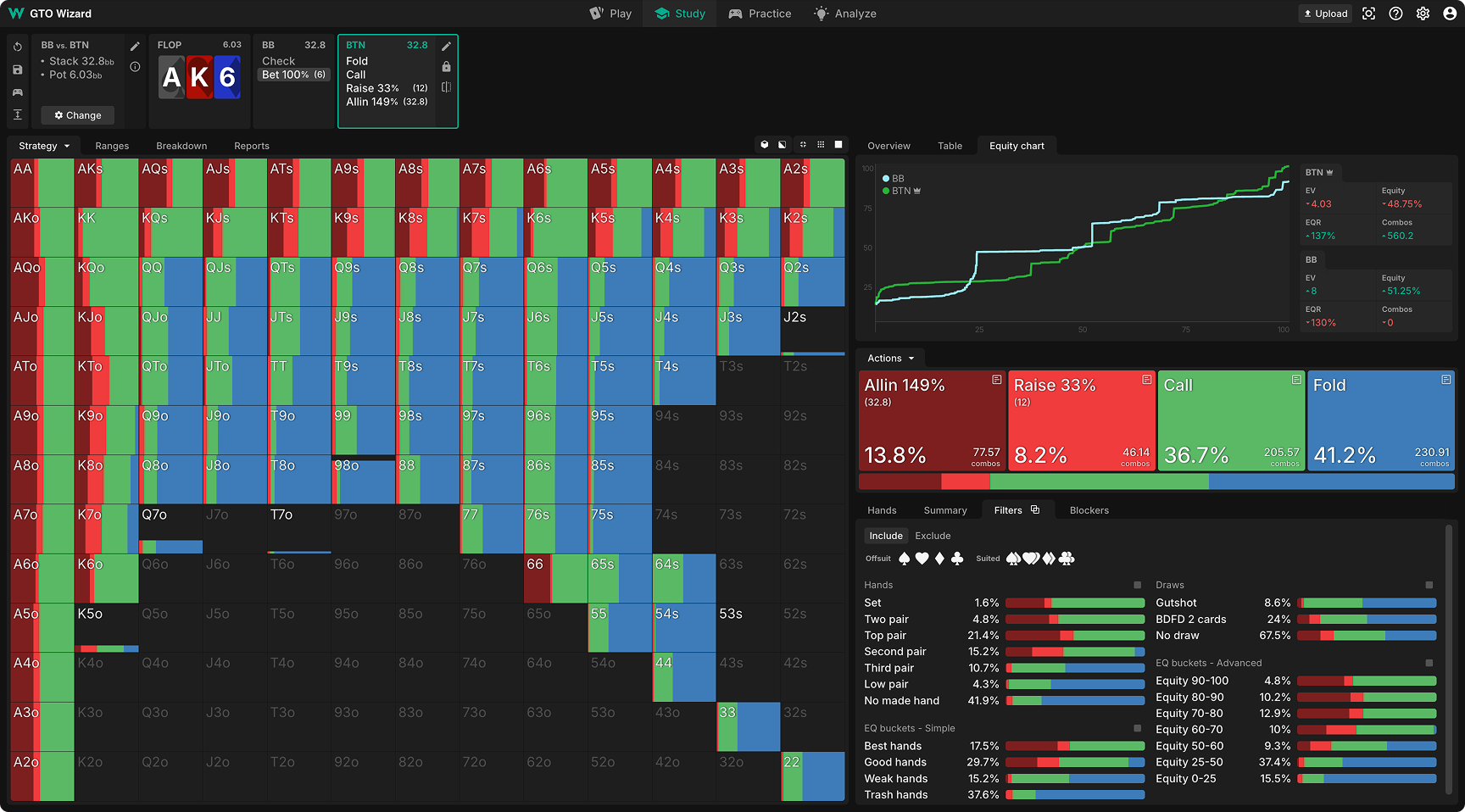
Situation:

BTN vs. BB single-raised pot, 35bb deep MTT. Flop comes AK6, which is fantastic for the preflop aggressor. The BB should check range here, but not everyone understands action flow. Instead, the BB leads out with a pot-sized bet. How would you respond in the BTN?

Nash Equilibrium: Apparently, we should respond by mixing folds with everything, folding 2nd pair sometimes and calling 8-high air sometimes. Furthermore, the raising strategy seems to be some wildly imbalanced mixture of value-heavy shoves and capped min-clicks. This is obviously nonsensical and, again, a result of non-convergence. The donk node was abandoned early in the solving process, thus the response is suboptimal.

BTN response vs BB’s 100% pot donk-bet on AK6r: Standard Nash

QRE: Provides a logical, clear, and converged solution. Call with hands that have strong outs against the top of BB’s range (e.g., King-x, 6-x, gutshots), fold your air, and leverage position effectively by using small raises. The hand selection and sizing are balanced, intuitive, and strategically sound.

BTN response vs BB’s 100% pot donk-bet on AK6r: QRE

QRE Benchmarks

Some players might be concerned when we say we are intentionally introducing mistakes into the strategy. However, to be clear, we fine-tune the “rationality” of the strategy so that it’s arbitrarily close to perfection.

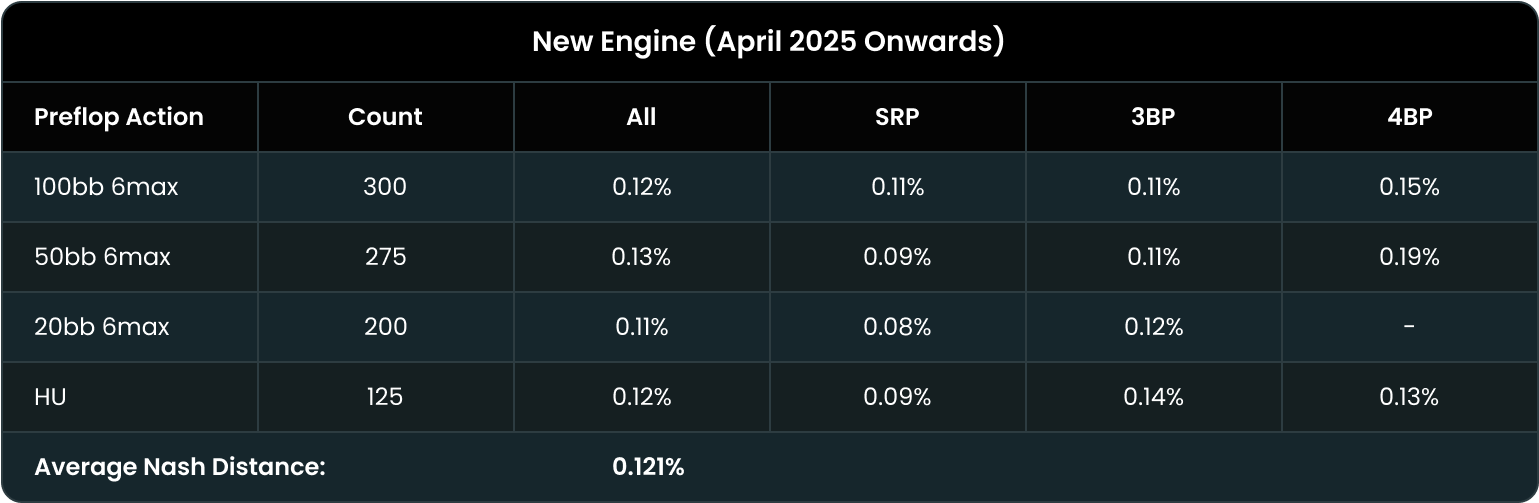
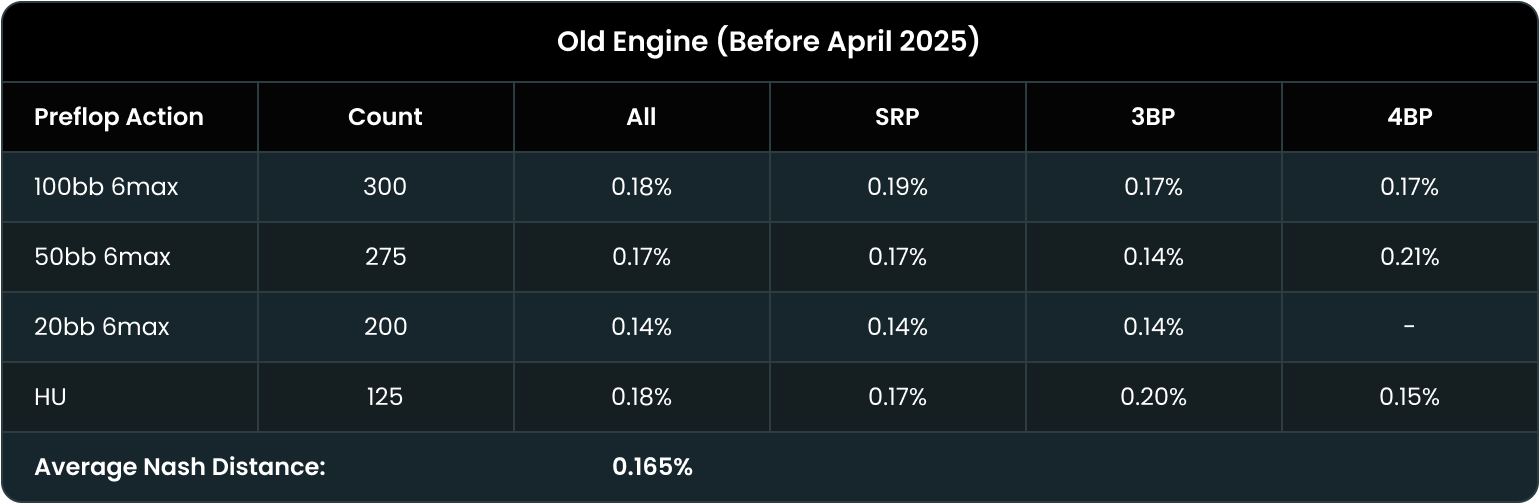
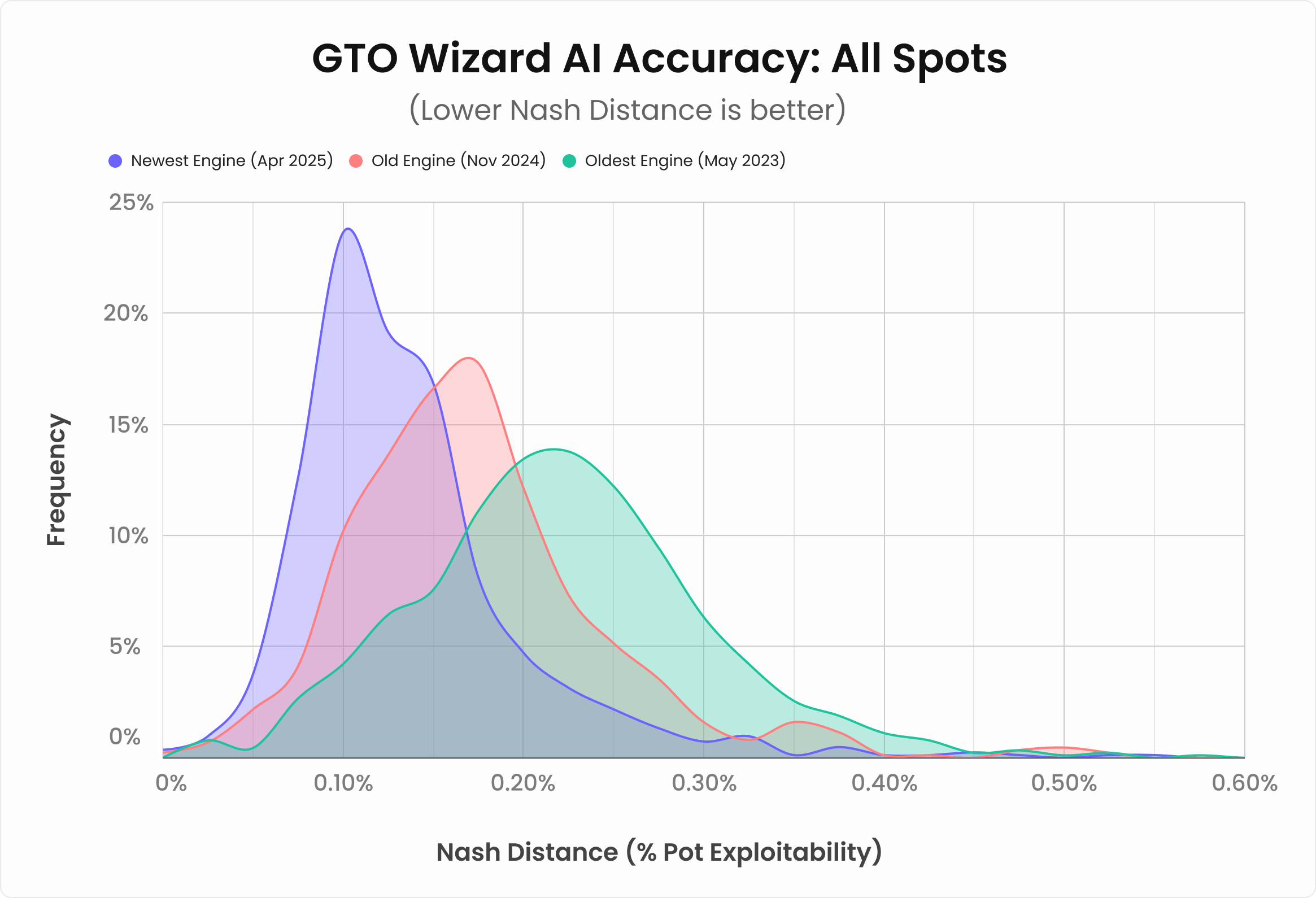
In fact, our newest engine isn’t just better against your opponent’s mistakes, it’s simply better all around. Over the last few months, we’ve upgraded our neural networks, showcasing significant reductions in the exploitability of our AI solutions. We show approximately a 25% reduction in the exploitability of our flop solutions, going from 0.165% to 0.12% exploitability as a percentage of the pot, on average!

What does that mean? Simply put, our latest engine produces solutions that are 25% more accurate than before, on average. Not only is QRE significantly better in ghostlines, but it’s better across the board:

Flop Exploitability:

Learn more about our exploitability benchmarks

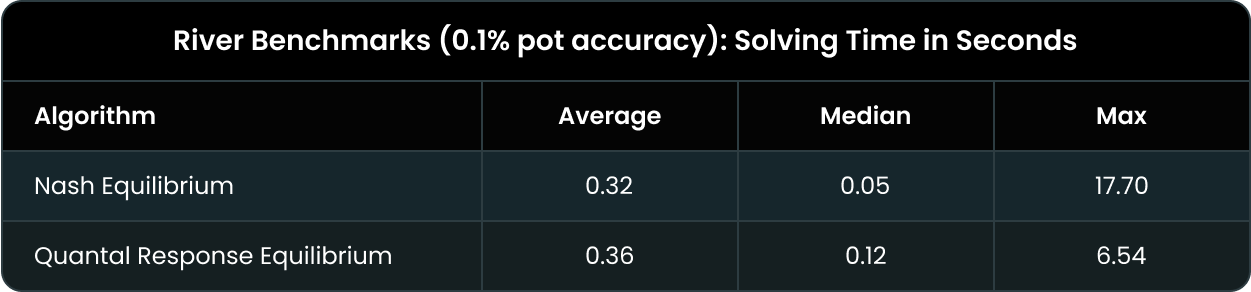
River Solving Time

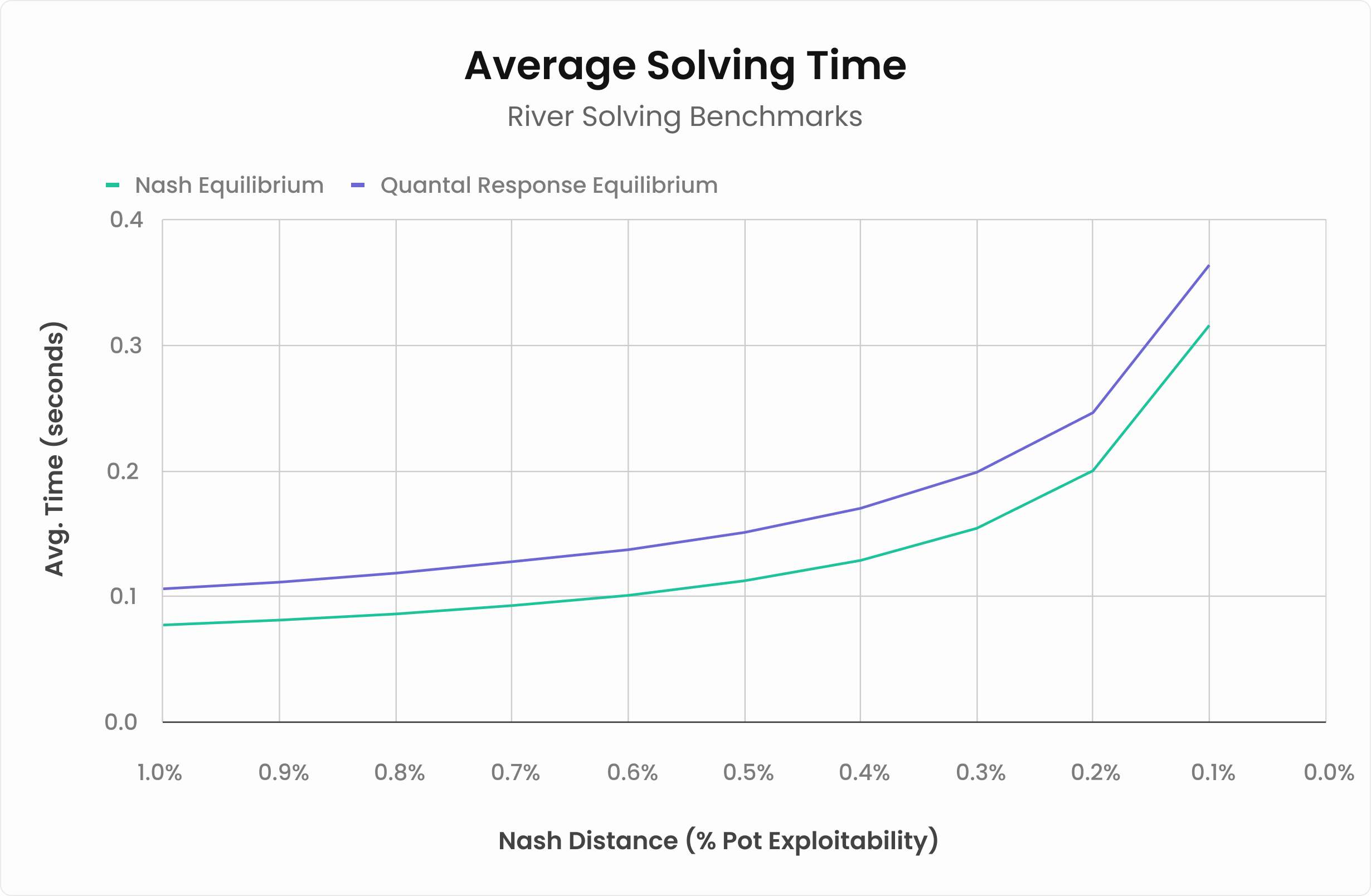
Another way to test the performance of these algorithms is to see how quickly it converges to a good strategy. On the river, we solve to an accuracy of 0.1% pot (meaning the river strategy is exploitable to at most 0.1% of the starting pot on the river).

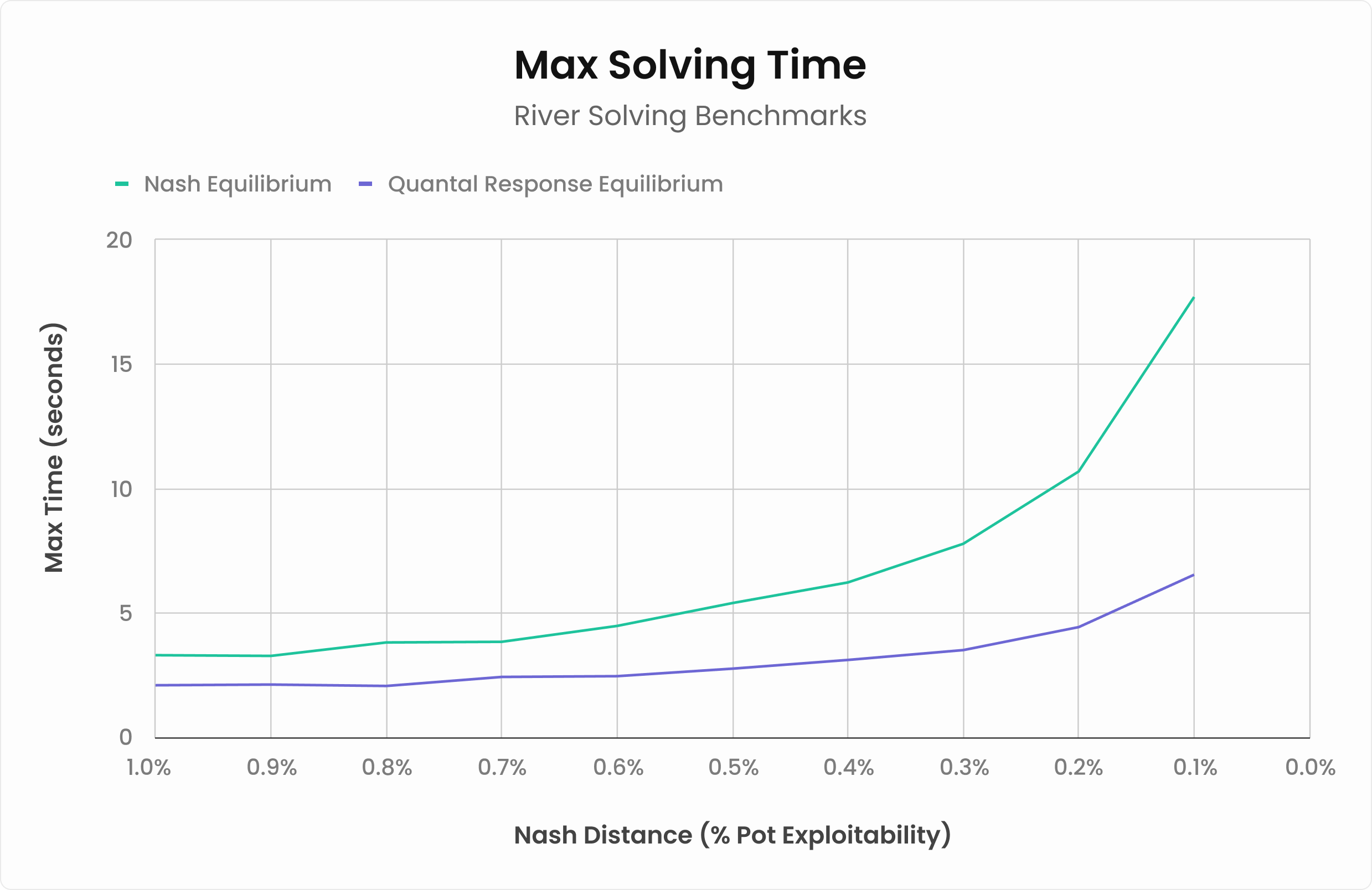
Our old Nash Equilibrium algorithm is very slightly faster, (0.32 vs 0.36 seconds), but you won’t notice a 40 ms difference. On the other hand, QRE tends to be significantly faster in very large spots (7 vs 18 seconds). Generally, QRE tends to be much faster in spots where you’ll actually notice.

Below, we graph how long it took each algorithm to achieve certain exploitability thresholds:

See Graphs

As you can see, QRE (blue) takes a fraction of a second longer to achieve the same exploitability as our standard Nash algorithm.

However, QRE (blue) performs considerably faster than the Nash algorithm in big complicated spots!

Measuring Performance In Ghostlines:
Tree Payoff Weighted Loss

Here’s the thing. The metric “exploitability,” AKA Nash Distance, doesn’t capture the key property of QRE: Better responses to ghostlines.

You see, if some spot is never supposed to happen in Nash, then it has no impact on the accuracy of a strategy. In theory, lines that aren’t supposed to happen have no impact on your EV and thus cannot be measured using traditional metrics like exploitability. But in practice, people are imperfect and make mistakes. In practice, ghostlines DO matter, and your response to these mistakes has a direct and measurable impact on your win rate. So, we need a way to measure performance that accounts for these low-frequency lines. To address this, we developed a new metric: Tree Payoff Weighted Loss (TPWL).

TPWL measures how well strategies perform across all nodes, treating each decision as equally important, regardless of the size of the pot, or how frequently that decision occurs. Please note that this is purely a method of evaluation rather than an assumption of actual gameplay frequencies.

Here’s how TPWL is calculated

In order to explain Tree Payoff Weighted Loss, we must first define the following terms first:

Best Decision

Payoff Weighted Loss (PWL)

Node Payoff Weighted Loss (NPWL)

The best decision a hand can make is the decision that maximizes EV for that hand, given that every other decision in the game tree is fixed. If two actions have equal EVs, then both actions (or any mix between them) are also the best decision for that hand.

Example: Suppose it checks to hero, HU IP on the river. Hero has the second nuts. If villain only ever calls the nuts after hero bets – then the best decision would be to check. This is regardless of what would occur at the Nash Equilibrium as the best decision is defined based on villain’s given strategy.

Payoff Weighted Loss (PWL) is the difference between the EV of the best decision of a hand and the EV of the chosen strategy of a player with that hand – divided by the value of winning the pot. Essentially, this is the regret of some action divided by the pot.

Example: Suppose hero is playing a rakeless cash game. The pot is 200. Against villain’s strategy, the EV of checking with Hero’s hand is 50, and the EV of betting pot is 100. Hero’s current strategy with this hand is to bet 90% of the time and check 10% of the time. So:

The EV of the best decision (betting pot) is 100
The EV of hero’s current strategy is 50 * 10% + 100 * 90% = 95
So hero’s payoff weighted loss with this hand is (100 – 95) / 200 = 0.025

Node Payoff Weighted Loss (NPWL) is the mean of the payoff weighted loss of every hand at a given node.

And, finally, Tree Payoff Weighted Loss (TPWL) is the mean of the node payoff weighted loss of every node in the game tree.

TPWL has three key benefits:

Equal Weighting: TWPL essentially treats every decision as equally likely. This reveals bad play in low-frequency spots.
Pot Normalization: TPWL adjusts for the size of the pot so that bad play in small pots cannot be hidden by good play in big pots.
Locality: NPWL at any node can be reduced to zero by adjusting only that node’s strategy, meaning poor performance in one node isn’t hidden by strong play elsewhere.

In essence, TPWL is a way to measure how well a strategy handles every possible scenario—especially those rare but potentially exploitable lines that traditional exploitability metrics overlook.

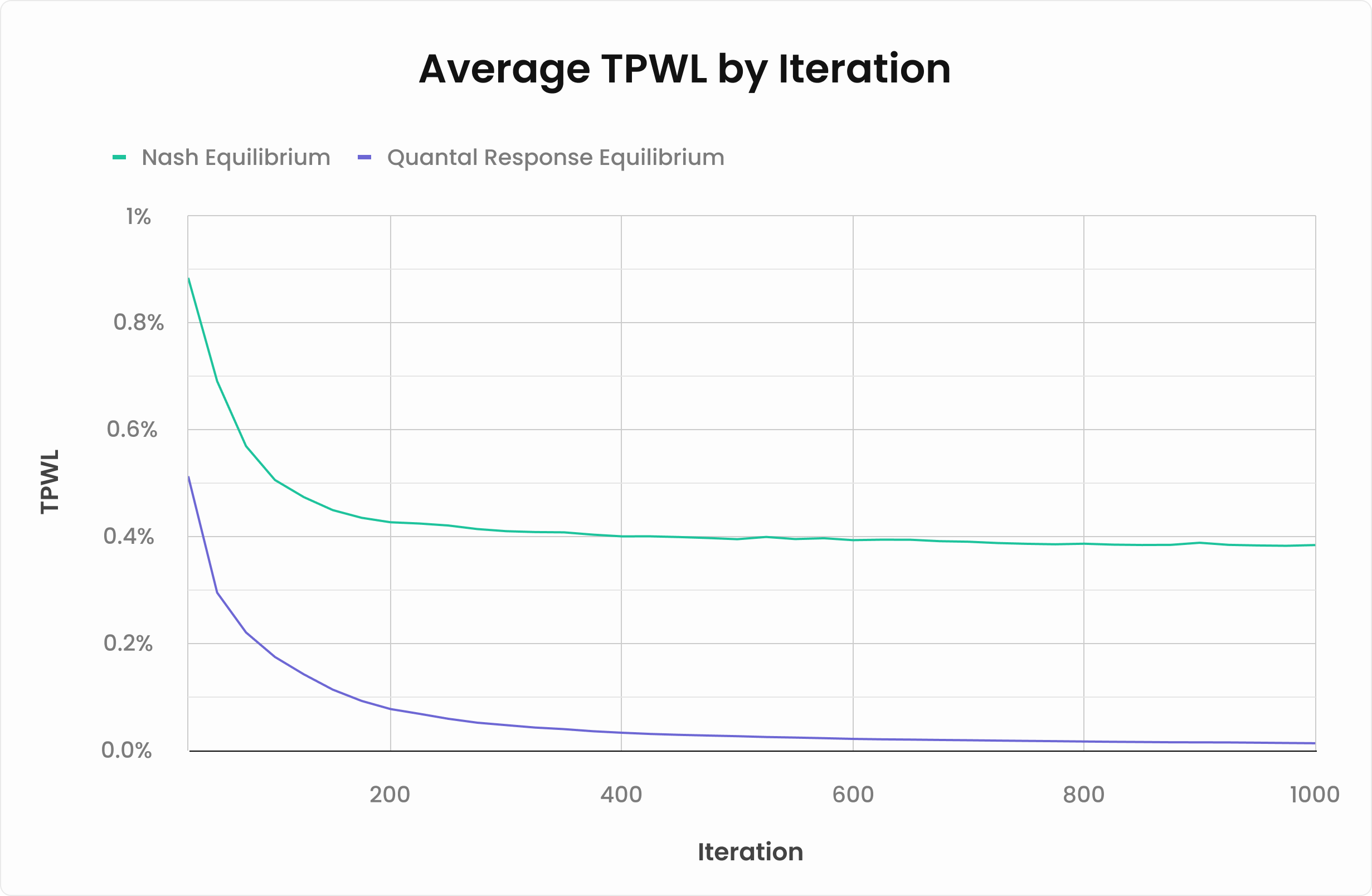
Quantal Response Equilibrium absolutely crushes Nash Equilibrium!

In short, measuring TPWL is a good way of answering the question, “How good is the quality of this strategy at each individual node in the tree?” Of course, exploitability is still the most important metric. However, having a low exploitability does not guarantee good performance in all nodes. If two strategies have comparable exploitabilities, the strategy that has a lower TPWL will perform better in a wider variety of situations. In practice, this means that a strategy with a lower TPWL will achieve a higher win rate against imperfect opponents.

To be clear, here we are calculating the TPWL on the river, comparing a traditional (tabular) NE solver with QRE. The NE solver caps out at about 0.38%, while the QRE solver quickly converges to 0.01%. This represents a 38x improvement.

Conclusion

Quantal Response Equilibrium is the natural evolution of Nash strategies. While Nash perfects normal lines, QRE optimizes every decision, including spots that aren’t “supposed to happen”. To put it simply, QRE outperforms Nash against opponents who make mistakes.

This solver upgrade isn’t just about better strategies today; it’s a crucial step toward solving more complex scenarios like multiway spots and non-zero-sum situations. Stay tuned; there’s so much more to come!

We’re Hiring

Curious how artificial intelligence is reshaping the future of poker? Check out this article: AI and the Future of Poker.

If you’re passionate about pushing the boundaries of technology, working on cutting-edge advancements, and unleashing the power of state-of-the-art machine learning algorithms, we want to hear from you. Join us in redefining how poker should be studied.