The Power of the Hypergeometric Bet

What size should we bet with our value and bluffs? When our range is perfectly polarized (with our value hands having 100% equity), many studied players know that our optimal wager is the geometric size: the fraction of the pot that gets us exactly all-in if we bet this same fraction on each remaining street. When used before the river, this geometric sizing enables our value hands to get all the money in while maximizing our opponent’s overall defense frequency. And while our bluffs do not benefit from the reduced fold equityFold equity
The amount of value a player will win by making another player fold., they recoup EV when our opponent calls on one street and folds on a future street, yielding us more than 100% of the initial pot.

Geometric bet size = the bet size in terms of the fraction of the pot that gets us exactly all-in if we bet this same fraction on each remaining street.

Less Than Geometric

In practice, our betting ranges will often be not perfectly polar. When we have a hand that is good but not great, betting the geometric size might be an “overplay,” tightening our opponent’s continuing range so that it contains too many better hands. As a result, we typically bet smaller than the geometric size with these thin value holdings, which sometimes comes with the side effect of folding out other hands in our opponent’s range that have equity.

More Than Geometric

In some unique situations, however, we should bet a hypergeometric size—a size larger than the geometric size. This is purely for the purpose of equity denialEquity denial
To fold out or “deny” your opponent’s equity. Any time you get your opponent to fold a hand that could have beaten you at showdown, you have denied them from realizing that equity. and accomplishes the following goals, many of which are interrelated:

We set ourselves up to go all-in before the river. When OOP, this mitigates our positional disadvantage by reducing the number of betting rounds.
By reducing the SPRStack-to-Pot Ratio (SPR)
The effective stack divided by the size of the pot. SPR is commonly used to gauge the value of implied odds and the relative value of made hands. more drastically than usual, we reduce the value of their implied odds with draws.
When the SPR is low, the geometric size may be too small so that it’s unable to make a substantial part of our opponent’s range indifferent. Most hands in their range will have some equity to outdraw even our strong value.
Betting a hypergeometric size with a mergedMerged
A merged range is often described as a range morphology between linear and polarized. Merged ranges often resemble polarized ranges with some medium-strength hands or polarized ranges with some bluffs. The purpose of “merging” is to make the range more robust. A perfectly polarized range is typically vulnerable to min-raises as you can’t call your pure bluffs, whereas a perfectly linear range may be vulnerable to overbets and continued aggression as your medium-strength hands can’t effectively realize their equity. A merged range attempts to reduce the exploitability of these extreme range constructions by including some medium-strength hands that improve flexibility. range manipulates the ranges of other actions, making them more polarized. This restricts our opponents from attacking these ranges with bets and raises, which they can do for a cheap price when stacks are short.

Hypergeometric bet size = a bet size that is larger than the geometric bet size.

In the rest of this article, we’ll apply the above concepts to a few example spots—in a 100bb cash game setting—where you should consider placing a hypergeometric bet.

Example 1: Preflop

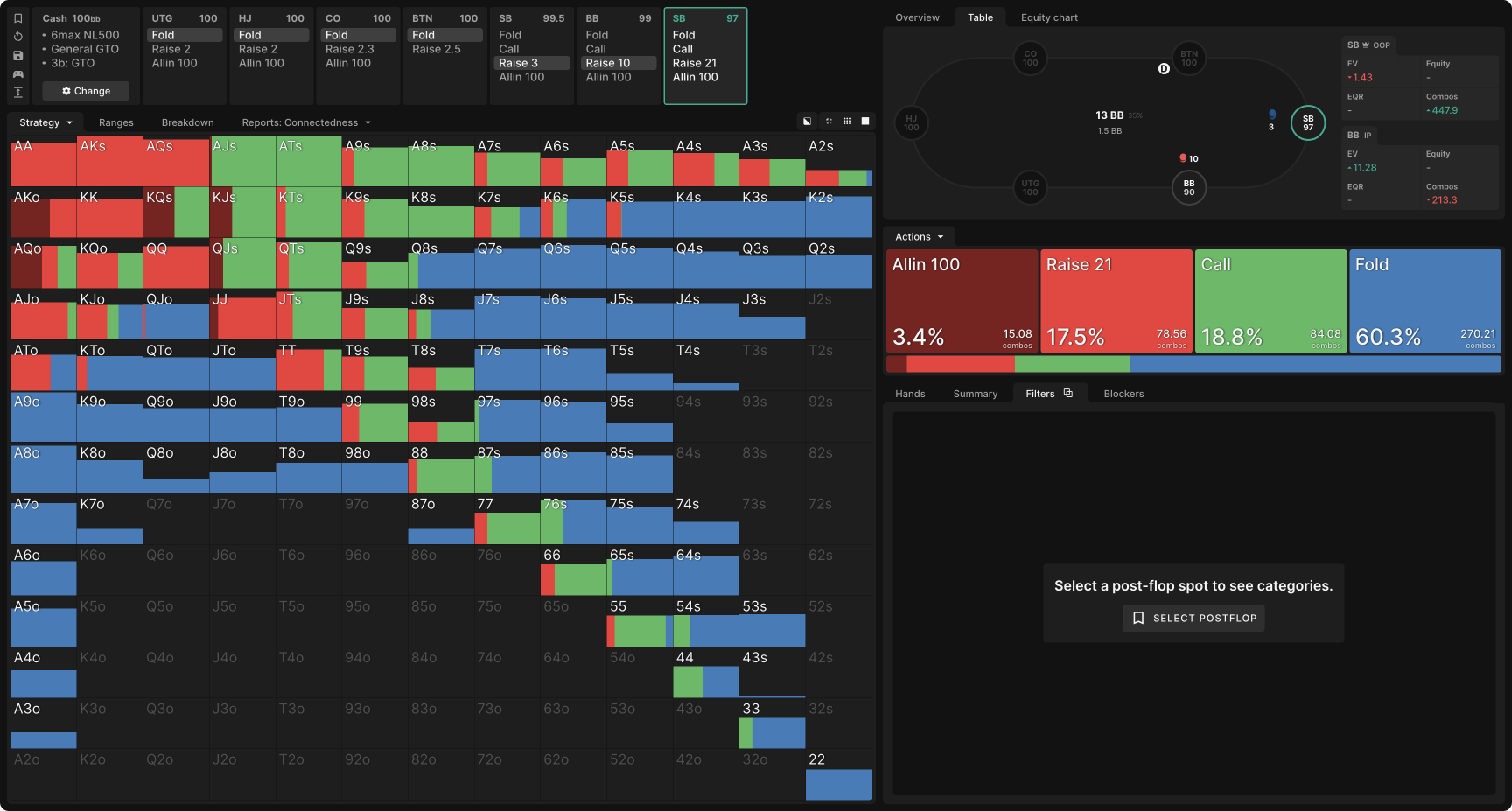
Suppose the SB open-raises (3bb) and gets 3-bet (10bb) by the BB. It might be surprising to you to learn that SB’s GTO strategy contains a significant frequency of 4-bet all-ins (100bb):

SB’s response vs BB 3-bet (100bb effective)

The hands that 4-bet jam make up a merged range:

JJ benefits from getting called by lower pocket pairs (TT–66) and folding out BB’s (unpaired) Ace-x, King-x, and Queen-x hands, constituting over 70% of BB’s unpaired 3-bets.
AKo benefits from getting called by AQ and folding out hands like 65s, which have over 40% in raw equity and plenty of implied odds.
AQo benefits from folding out similar low, suited hands while having close to 50% equity when most pocket pairs call.
KQs, KJs, and QJs benefit from folding out dominating hands (AQo, KJ, AJ) while, again, having close to 50% equity when called by most pocket pairs.

None of these hands are pure “value” or “bluffs”: each of them derives some EV from BB calling hands that it has decent equity against, and some EV from BB folding hands with decent equity against it.

Furthermore, SB’s choice to implement 4-bet all-ins accomplishes the goals mentioned in the introduction:

It allows SB to play postflop less often with a positional disadvantage.
SB prevents hands like AQo and 54s from realizing their implied odds when they hit top pair or better.
A small (~20bb) 4-bet size allows BB to continue every decent suited hand with which they 3-bet. Alternatively, a large (~30bb) 4-bet would give BB too cheap a price on a 5-bet shove, so employing an all-in 4-bet size makes sense.
By 4-bet jamming with a merged range, the range with which SB 4-bets smaller becomes more polarized. This increases their postflop EV in 4-bet pots. For example, on Queen-high boards, SB’s range will be more concentrated toward top pair+.

Example 2: Flop

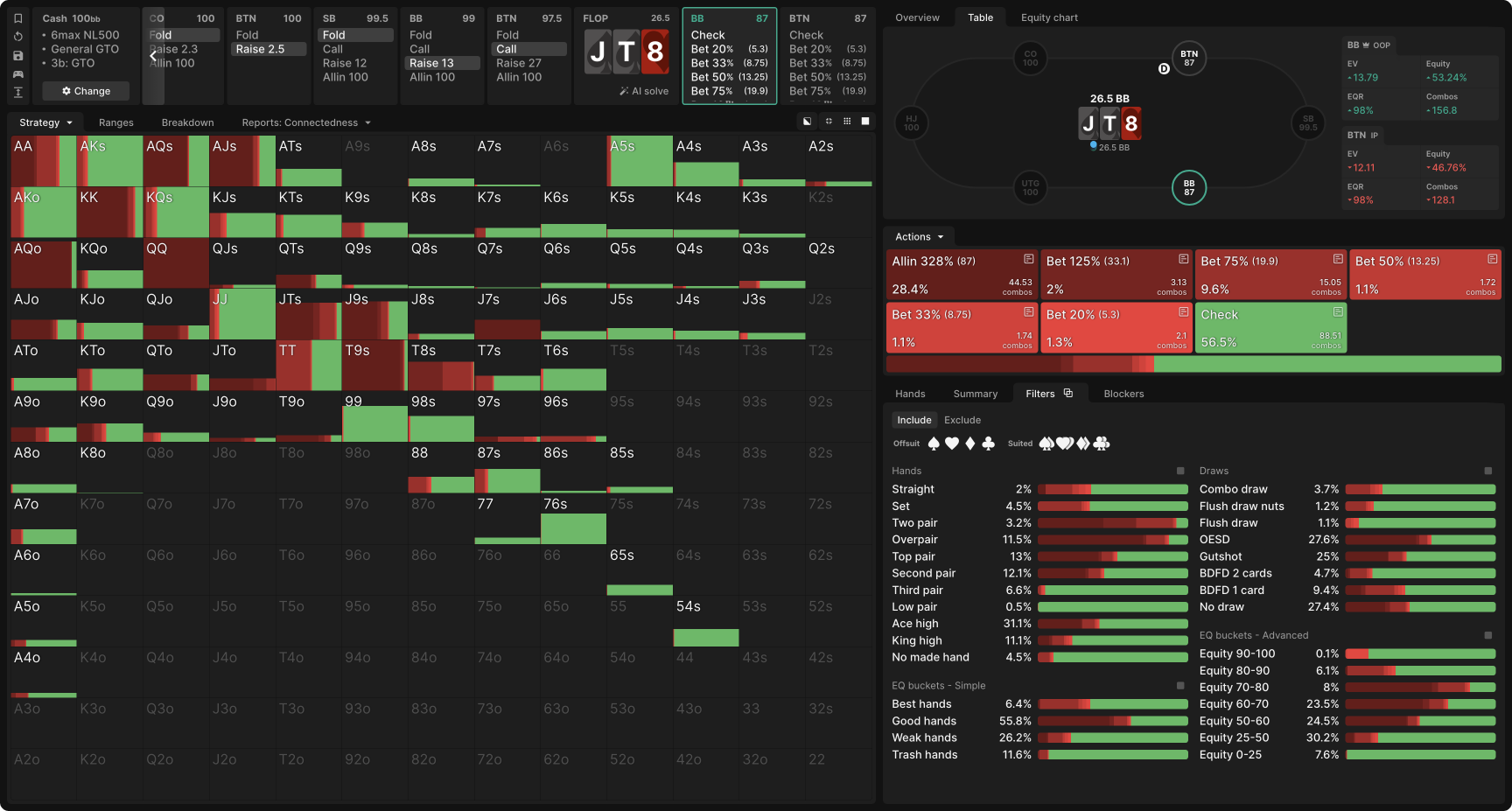
Suppose the BTN open-raises and gets 3-bet by the BB, the BTN calls, and the flop comes J♠T♠8♥. Astonishingly, BB should shove for over 3x pot around 28% of the time:

BB’s flop strategy on JT8tt vs BTN in a 3BP (100bb effective)

Again, the hands with which BB jams make up a merged range, which we can subdivide into three main regions:

Top pair top kicker and better: This can be considered BB’s “value region,” with AA, KK, QQ, and AJ being frequent jams. By going all-in, these hands get called by BTN’s weaker pairs. As a side benefit, they fold out strong draws such as 99 (no spade), AQ, A♠5♠, and KQ, hands which have at least 10 live outs. Note that sets are too strong to jam. Further, if the BB shoves with J♥J♦, we can see from the ‘Blockers’ tab that holding these two cards decreases BTN’s calling frequency by ~3.2%. Assuming for simplicity that J♥J♦ loses 50bb in expectation when BTN folds (compared to when BTN calls), the EV of shoving this combo is reduced by around 1.6bb due to its blockers—a significant decrease.
Weak top pair and second pair: Because this board is so dynamic, these hands serve as both value bets and bluffs: they can obtain folds from better made hands and calls from worse hands (characterized by having some form of draw). For example, by shoving T♦9♦, BB gets BTN to call with 9♠9♥ and 9♣8♣, yet gets BTN to fold K♥T♥ and K♦J♦—a huge win.
Draws: This region of hands revolves around AQ, which bluffs off many of BTN’s single pair hands and has 8–14 outs against BTN’s best calls. On the rare occasion that BTN has a nut flush draw, AQ can even get called by a dominated hand.

Example 3: Turn

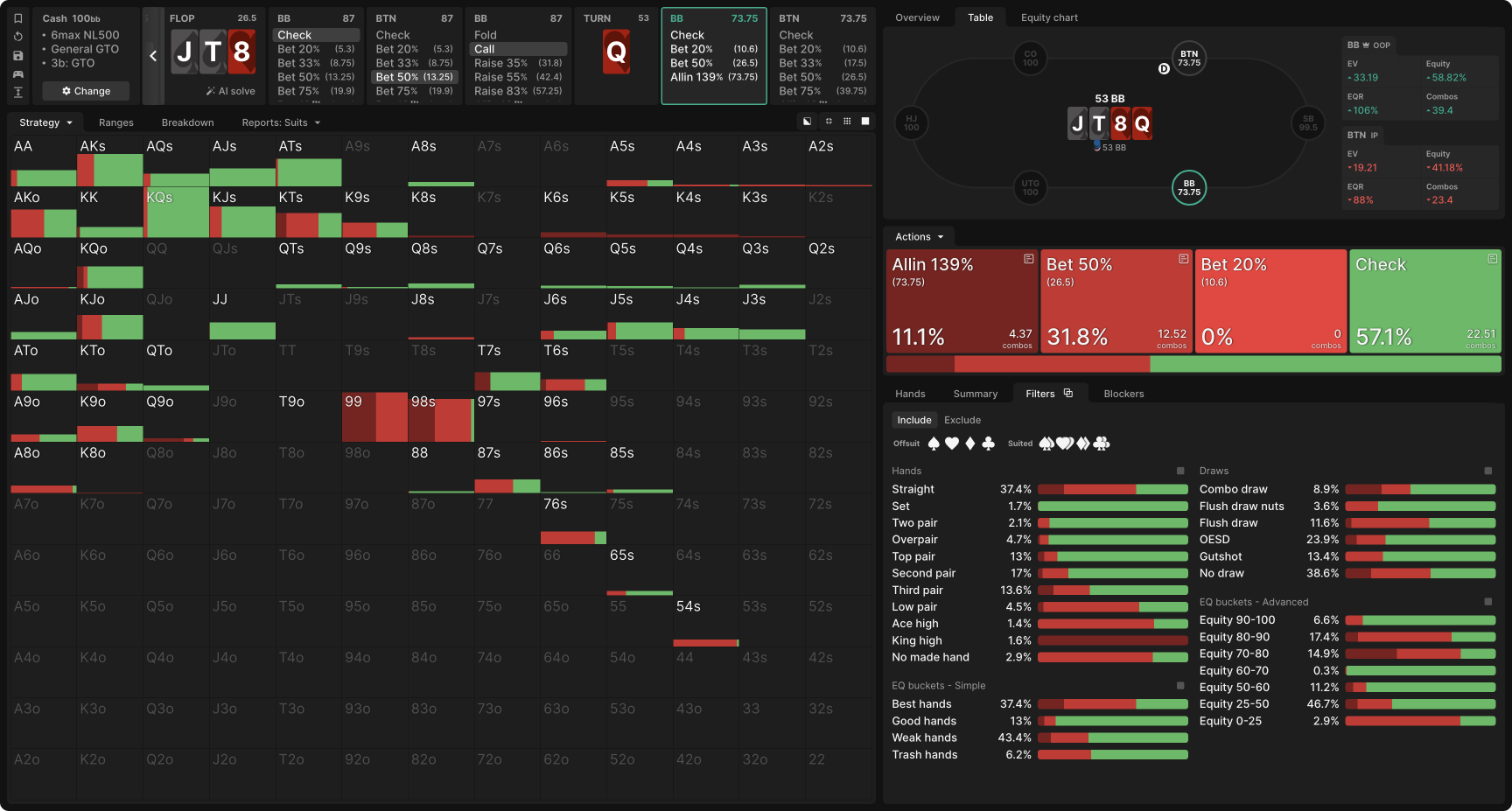
Consider the same setup as in example 2, but instead of c-bet jamming the flop, BB check-calls a half-pot bet, and the turn is the Q♥:

BB’s turn strategy (after check-call flop) on J♠T♠8♥ Q♥ vs BTN

The BB adopts a donk betting strategy, including both a geometric (50% pot) and a hypergeometric (all-in for 139% pot) size! A whopping 37% of BB’s range makes a straight (compared to 20% for the BTN).

Conclusion

The geometric bet size is designed to maximize the amount of money your opponent puts into the pot, so that you can get the most value with a perfectly polarized range. However, in practice, there is no such thing as a “perfectly polarized” range. Before the river, most hands have outs to outdraw each other.

The hypergeometric bet size exists to fold out draw equity. Rather than maximizing your opponent’s call-down range, it can sometimes be worth it to force them to fold more often, in order to deny equity.

Wizards, you don’t want to miss out on ‘Daily Dose of GTO,’ it’s the most valuable freeroll of the year!

Sharpen Your Game With Our Most Customizable GTO Trainer Ever

We Are Hiring

We are looking for remarkable individuals to join us in our quest to build the next-generation poker training ecosystem. If you are passionate, dedicated, and driven to excel, we want to hear from you. Join us in redefining how poker is being studied.

Check out the available positions here.

GTO Wizard the #1 App for Poker players

Study any spot imaginable

Practice by playing vs. GTO

Analyze your hands with 1-click

START CRUSHING NOW

JOIN DISCORD