Variance and Bankroll Management

Vital Soft Skills for Every Poker Player

Despite our best efforts to maximize our edge at the tables, at its core poker is a gambling game. It is beatable, but it is still built around the same foundational pillar as every other casino game: crazy, gut-wrenching, mind-numbing variance!

Watch the video

Is Poker Luck 🍀 or Skill?

Both! How much luck or skill depends on how many hands you play. Tiny edges get magnified in the long run. In the short run your results are mostly dictated by luck. But even a small edge over a long enough timeline becomes inevitable. Your results are mostly dominated by luck in the short run, and by skill in the long run!

What Exactly is Variance?

The term variance refers to a statistical measurement of the spread between numbers in a data set. In poker, variance refers to how “swingy” your results are!

In higher variance games, a player’s results can deviate further away from their expectation over a given sample.

Variance is measured with the “Standard Deviation” metric. You can find this metric in most poker HUDs, but it can also be calculated directly from your results. For cash games, this is measured in BB/100.

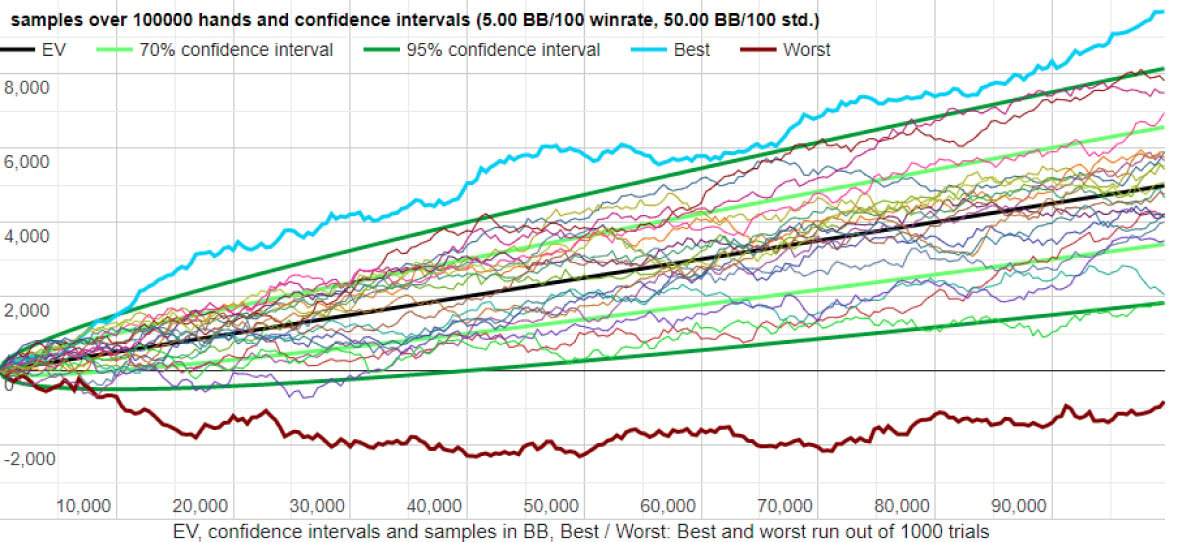
Let’s look at some examples. The following charts are examples of 20 random runs given a set of inputs (credit: Primedope)

Low Variance results

Note that the best and worst runs are between -1,000 BB and +10,000 BB.

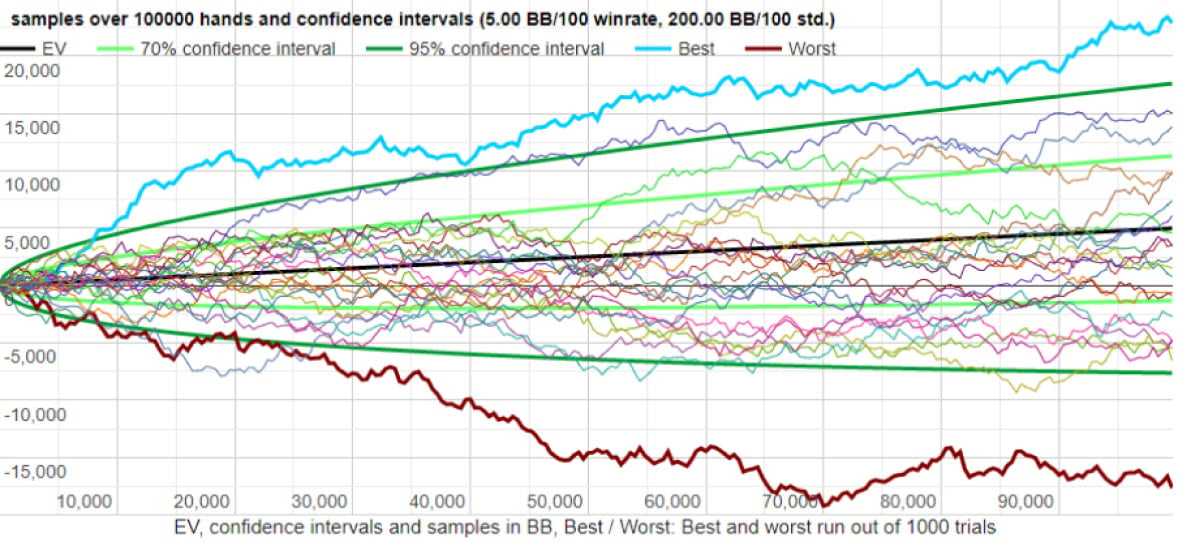
High variance results

Note that the best and worst runs are between -17,000 and +22,000!

Both players have an identical win rate, but the higher variance player has a much larger spread between their best and worst runs!

The law of large numbers

The gambler’s fallacy is very common among poker players. Let’s say we flip a fair coin, and it lands on heads 6 times in a row. What is the probability that it lands on heads the next flip?

If you’re superstitious, you might think you are “owed” tails. But that’s simply not how reality works. The next flip is 50%/50%. You’re just as likely to flip a 7th heads as you were to flip heads the first time.

After thousands of flips, we would expect heads and tails to even out. But that’s not because of some universal Karma; it’s simply the law of large numbers. Imagine we flip 1000 times and heads retains the 6-flip lead. At this point, we’ve flipped 503 heads and 497 tails – this is actually the expected value when starting with a 6-point lead. At this point, it’s 50.3% heads, 49.7% tails.

Now imagine we flip 100,000 times and retain the same 6 point lead. Now it’s 50.0003% heads and 49.9997% tails. The “luck” appears to even out despite tails never catching up. This is the law of large numbers.

Similarly, just because you’ve had bad luck doesn’t mean you are “owed” any rungood. The deck owes you nothing. Each hand is an independent event without memory of how you got your aces cracked.

The opposite is also true. Just because you’ve run well doesn’t mean you’re owed any bad luck. The truth is that variance in poker is far beyond what humans are capable of truly conceptualizing. If you’ve ever played around with a poker variance calculator, you’d find that it takes tens of thousands of hands before you can see a statistically significant edge materialize.

Confidence intervals

One of the most common questions we see is “how many hands do I need before I can be sure of my win rate?”. The problem with this question is that it doesn’t have a real answer. In math, we use confidence intervals to address these unknowns!

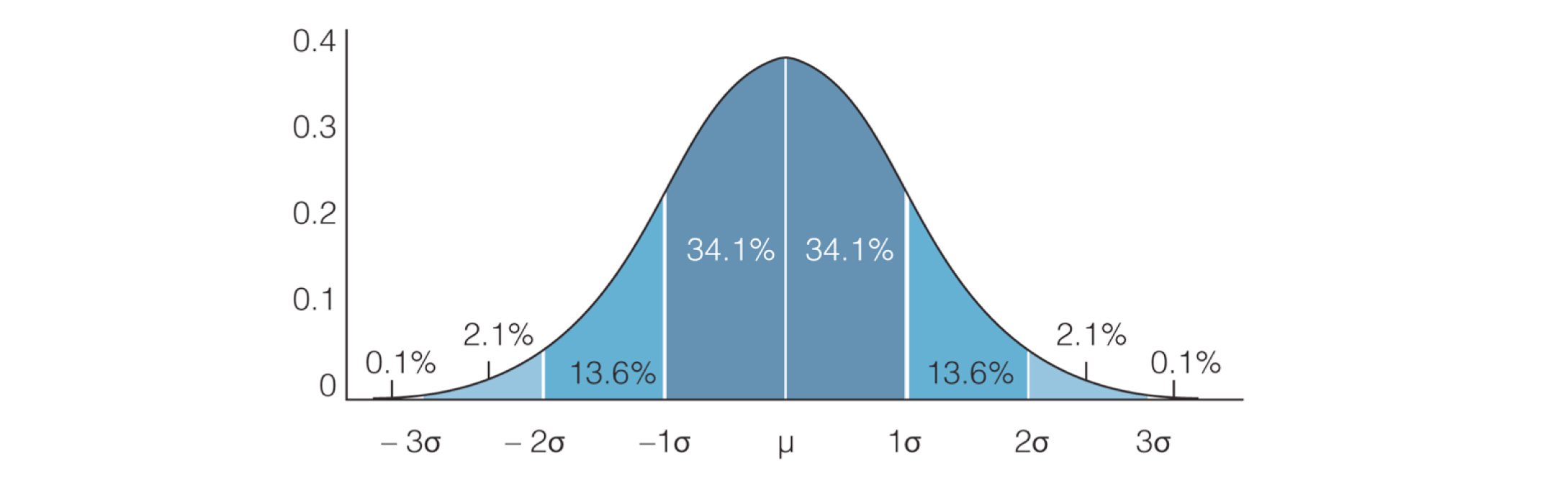
Confidence intervals follow the 68-95-99 rule:

68% of the time your results will fall within 1 standard deviation σ of the mean
95% of the population is within 2 standard deviations (2σ) of the mean
99.7% of the population is within 3 standard deviations (3σ) of the mean

Distribution of Variance

μ = Expected Value

-1σ to 1σ = 1 Standard Deviation (ie: ~2/3 of the time, your results will fall within this range)
-2σ to 2σ = 2 Standard Deviation (ie: 95% of the time, your results will fall within this range)
-3σ to 3σ = 3 Standard Deviation (ie: 99.7% of the time, your results will fall within this range)

Let’s look at an example:

Let’s assume your “true” (mean) win rate is 2.5 BB/100. This is your expected value.
Your standard deviation (σ) after 100k hands is 3.16 BB/100.
A better way to write your win rate would be:

2.5 ± 3.16 BB/100. (Winrate ± σ)

In other words:

70% of the time (~1σ) your results will fall between -0.66 BB/100 and 5.66 BB/100
95% of the time (2σ) your results will fall between -3.82 and 8.82 BB/100

In science, unknown variables are assigned margins of error and confidence intervals rather than exact numbers. Your win rate is an unknown variable. Therefore, it’s impossible to assign an exact number. The best you can do is assign some margin of error.

The formula for your margin of error is a function of your standard deviation and volume. Putting in more volume, or lowering your variance, will lower the margin of error and increase the confidence of your results. The formula is as follows:

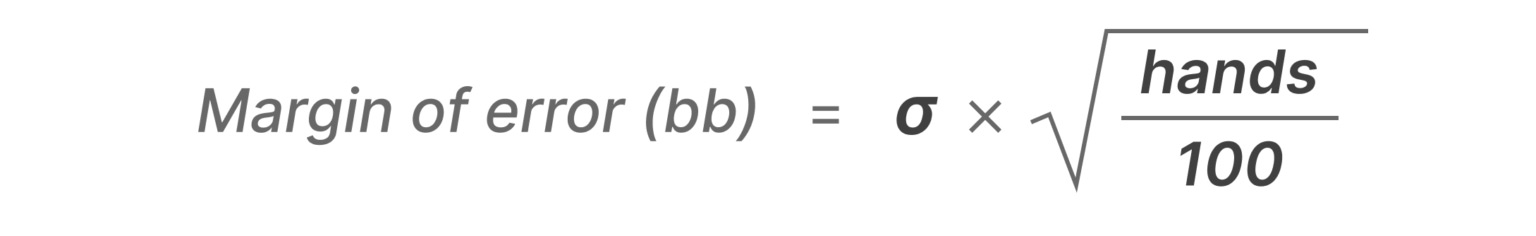
Where σ is your standard deviation in BB/100, and hands is simply the number of hands you’ve played. For example, above we see a standard deviation of 100 BB/100, and 100k hands played. 100 * (100,000/100)^0.5 = 3162. In other words, the results are plus or minus 3162 BB, or 3.16 BB/100. This is shown as “standard deviation after 100000 hands” in the above picture, but it’s easier to think of this as a margin of error.

Managing Risk

Variance can be calculated by free computer programs based on the aforementioned inputs.

Some recommended websites for this purpose are Primedope and ReviewPokerRooms. Understanding the bounds of variance is a great way to put your results and expectations in context. Spending some time playing around with different inputs yourself and seeing the resulting outputs is invaluable.

The above tools are for cash games 💸. MTT players tend to experience even greater variance. Try this MTT Variance calculator!

Bankroll management guidelines

The purpose of this article is to give you the tools to build your own bankroll management strategies, rather than prescribing some answer. Your BRM is a function of your risk profile. However, we’ve outlined some very basic BRM guidelines below based on common wisdom:

For cash players: 35 to 65 buy-ins

Never risk more than 5% of your roll

For tournament players: 75 to 125 buy-ins

Never risk more than 2% of your roll

Kelly Criterion

The Kelly Criterion tells you what portion of your bankroll you should risk. It considers your edge and odds on a bet and outputs how much of your bankroll you should risk.

“The core of bankroll management strategy is to maximize your edge without overplaying your roll. This is what Kelly does.”

The formula for the Kelly Criterion is outlined as follows:

f = the fraction of bankroll to bet
b = the decimal odds – 1
p = the probability of winning
q = the probability of losing, which is 1 – p

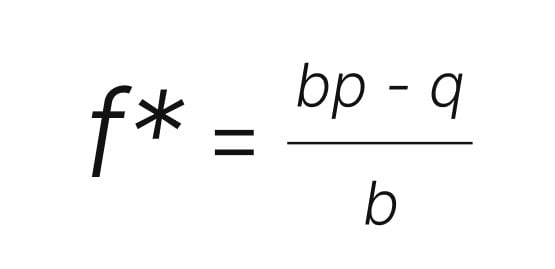
Let’s try an example

You play HU SnG and average a 5% return on investment (ROI).
Your bankroll is $1000.
What stakes should you play to grow your bankroll as fast as possible?

A) $100 buy-in
B) $50 buy-in
C) $25 buy-in
D) $10 buy-in

🎲 Answer

B) $50 buy-in

The basic premise of the Kelly Criterion is that you should risk your edge! For a simple 1:1 wager, if you have a 5% edge, you should risk 5% of your bankroll, which comes to $50 in this example.

Here’s how to solve this with math:

b = 1
p = 52.5%
q = 47.5%
f* = p – q = ROI
f* = 5%
5% of $1000 = $50

This is based on a “Full Kelly” strategy. A full-kelly strategy is like redlining your engine! In practice, it’s often better to implement half-kelly or even quarter-kelly strategies. A half-kelly strategy captures 75% of the growth while only taking on 25% of the variance. So C) $25 BI might be a better answer in practice.

Optimal Bankroll Management Strategies

The Kelly Criterion tells you what portion of your bankroll you should risk. How much you should risk depends on your win rate and variance. Just remember that Kelly is the boundary, not the goal! You should invest less than Kelly in practice.

We can use math to translate a poker win rate in Cash Games or other formats to optimal BRM strategies. We’ve built a handy BRM Optimization tool to help you move up faster! 💪

This calculator finds the minimum bankroll required to justify moving up stakes and taking on more variance in exchange for a higher hourly win rate.

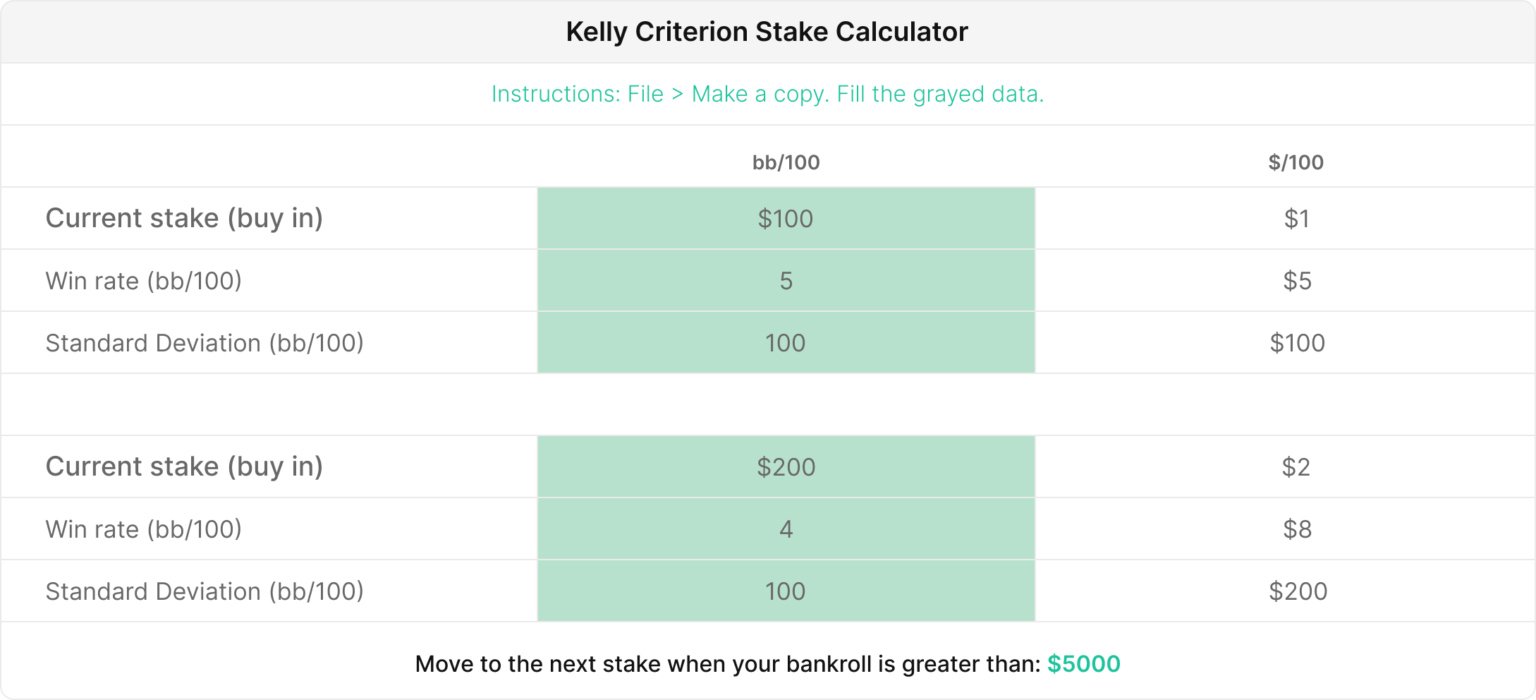
We’ve also included a (beta) calculator for MTT players! Kelly becomes more complicated for bets with multiple outcomes (tournament placements). Some outcomes result in huge changes to your bankroll, while others are quite small.

Maximize this equation to find the optimal BRM strategy in MTTs:

f(x) = probability₁log(outcome₁) + probability₂log(outcome₂) + probability₃log(outcome₃) + …

Where:

Probability represents the probability of each placement in the tournament.
Outcome represents the fractional change of your bankroll for some placement in the tournament. For example, if placing first would increase your bankroll by 20%, then that outcome is assigned a value of 1.2. If busting decreases your roll by 1%, that outcome is assigned a value of 0.99.
Add a term for every possible outcome in the event.

In practice it’s quite difficult to assign values to this equation, but we can estimate the probabilities given some edge (ROI). Note that the 100BI rule is far too aggressive for most large field MTT’s!

Tilt

Tilt is defined as taking a suboptimal action due to emotional distress rather than a rational justification. Many poker players succumb to tilt when on a downswing due to fear of losing more money or a desire to win back previous losses.

Tilt can be very dangerous since, as demonstrated above, decreasing your win rate will result in greater variance. This becomes a self-fulfilling prophecy and further extends the duration of downswings.

We’ll discuss more about tilt management in later articles.

Conclusion

If there is one thing to take away from studying poker variance, it is that the old adage “don’t gamble with money you can’t afford to lose” holds true.

We hope that as you learn more about variance, it will help you gain a better understanding of the temporariness of upswings and downswings and improve your mental state as you advance in your poker journey.

GTO Wizard the #1 App for Poker players

Study any spot imaginable

Practice by playing vs. GTO

Analyze your hands with 1-click

START CRUSHING NOW

JOIN DISCORD