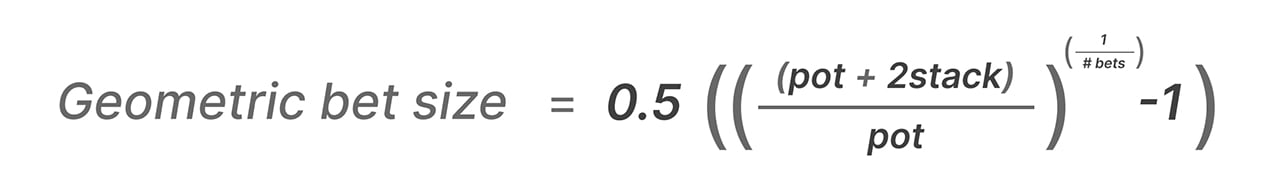Pot Geometry

What is Pot Geometry?

“Pot Geometry” refers to betting an equal fraction of the pot on each street, such that you’re all in by the river. This betting strategy is also called the “geometric bet size” or “geometric growth of the pot” (GGOP).

Betting geometrically has one major effect: This strategy maximizes how much money your opponent puts into the pot. If you want to get all the money in by the river, then betting geometrically will force the widest theoretical defence from your opponent.

In this article we’ll explore the theory of pot geometry, why it causes the opponent to defend wider, go through examples, and discuss the limitations of this betting strategy.

Maximize how wide villain defends

Why does betting geometrically maximize how wide villain calls?

There are an infinite number of betting strategies that can accomplish this. You can bet huge then small then medium. Or overbet twice. Or check->check->shove. But what betting strategy is most effective at making villain call widest? The Geometric bet size, of course!

Betting the same fraction of the pot on each street will theoretically maximize how wide villain calls overall and how much money gets contributed to the pot on average.

But why? 🤔

We can estimate how wide villain defends using Minimum Defence Frequency (MDF). Multiply the MDF on each street to find the final calling range.

Strategy B has villain donating almost twice as much money to the pot, which doesn’t even include the money they call on earlier streets and that fold before showdown. If you account for that, then villain’s total contribution is closer to $237.

How many streets?

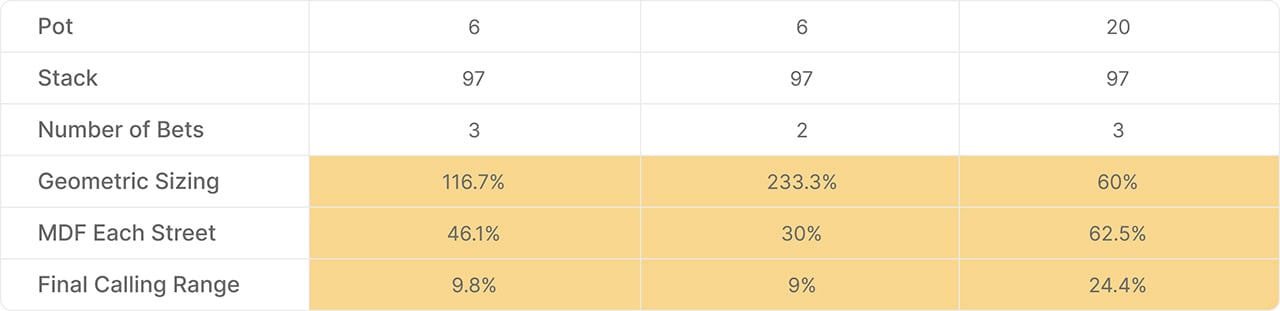
Pot is $6
Stack is $97

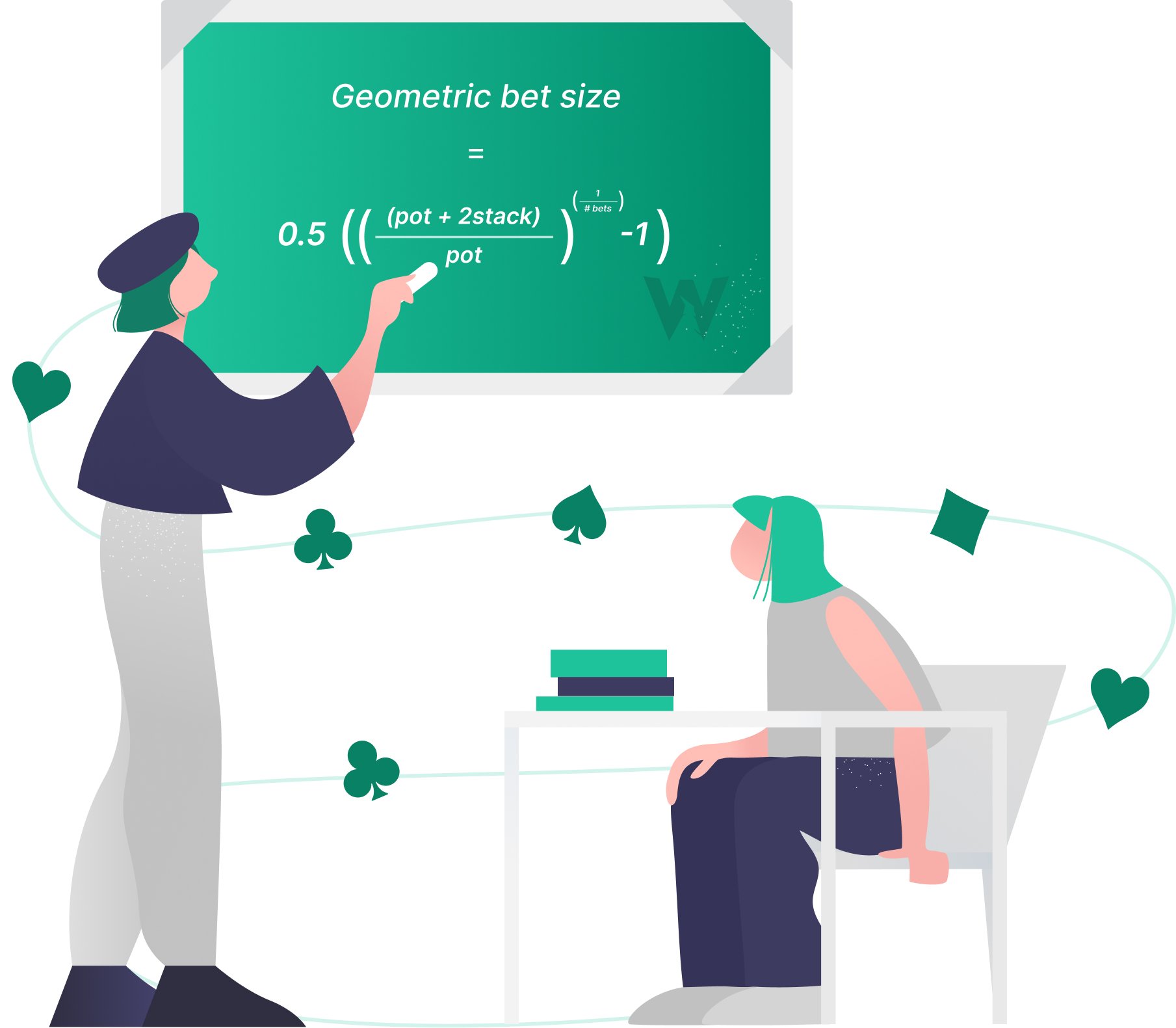
The geometric bet size is a function of how many streets (bets) remain. Fewer streets require larger sizes to get money in by the river:

The general formula for finding the geometric bet size is as follows:

Calculating this in-game is overkill, though. It’s best to simply estimate the geometric size by thinking about the size of the stack and pot by the river.

Betting smoothness

Let’s define the “smoothness” of your betting strategy as the standard deviation of all your bet sizes (in pot%) on every street.

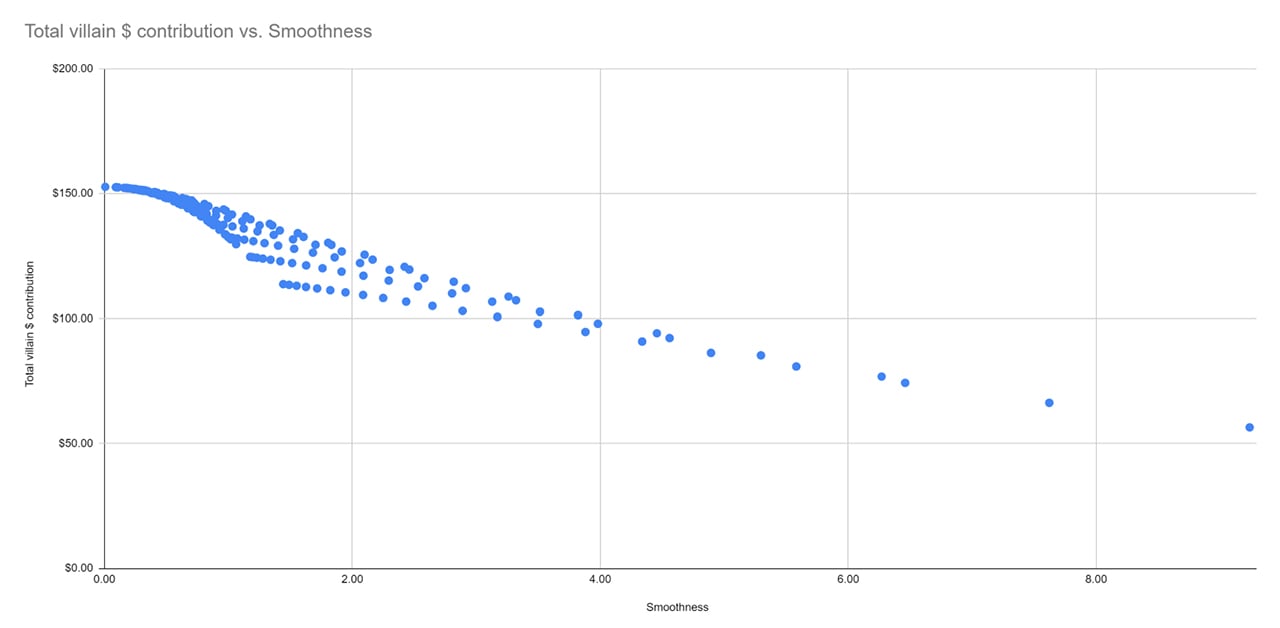
Here we’ve created a spreadsheet with 400 different betting patterns, all of which get money in by the river. Next, we’ll graph the smoothness of a bet against the total amount contributed. We can see from the graph below that the smoother the betting strategy, the more money goes into the pot.

The verticle axis represents how much money villain puts into the pot. The horizontal axis represents the standard deviation (spread) between our flop/turn/river bet sizes.

Villain’s calling range widens proportionally with the smoothness of our bets. The further our betting pattern deviates from geometric the less they are required to call us down to deny us a profitable bluff.

This is why you stack off tighter when playing deeper. Nut advantages are more valuable as stack-off ranges tighten.

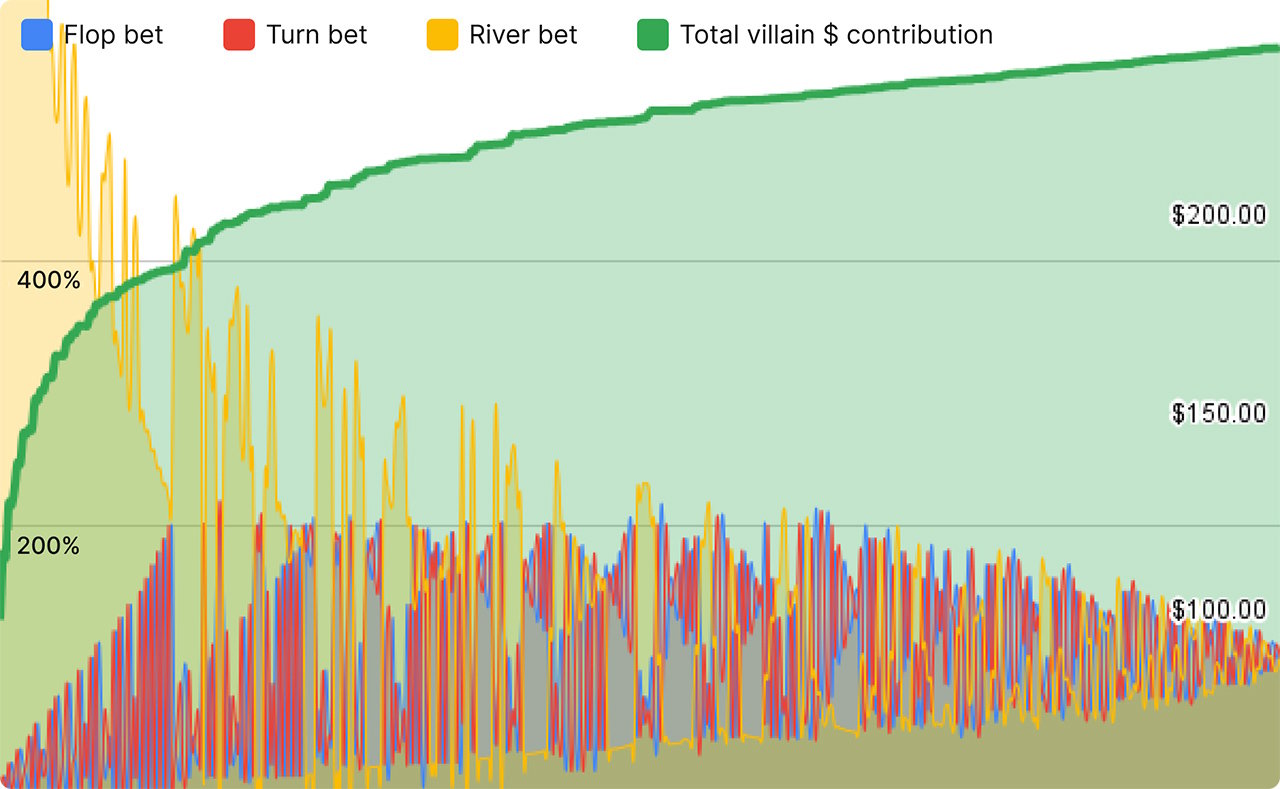
Next, we’ve graphed different betting strategies against how much money villain puts into the pot. Note that villain contributes the most money to the pot when our flop/turn/river bet sizes are the same (as a percentage of the pot).

Explore this data

We’ve linked the spreadsheet here so you can play around with the data. You can try different stack and pot sizes.

When to bet geometrically

Game theory optimal strategies typically use geometric bet sizes when they want to maximize value with a big nut advantage. This works best when your range is polarized and your opponent’s range is capped.

The geometric betting strategy is derived from MDF, which only really holds true in a polarized vs bluff-catcher toy game. However, you should still bet geometrically when you have a big nut advantage.

One of the most common examples are turn probe bets.

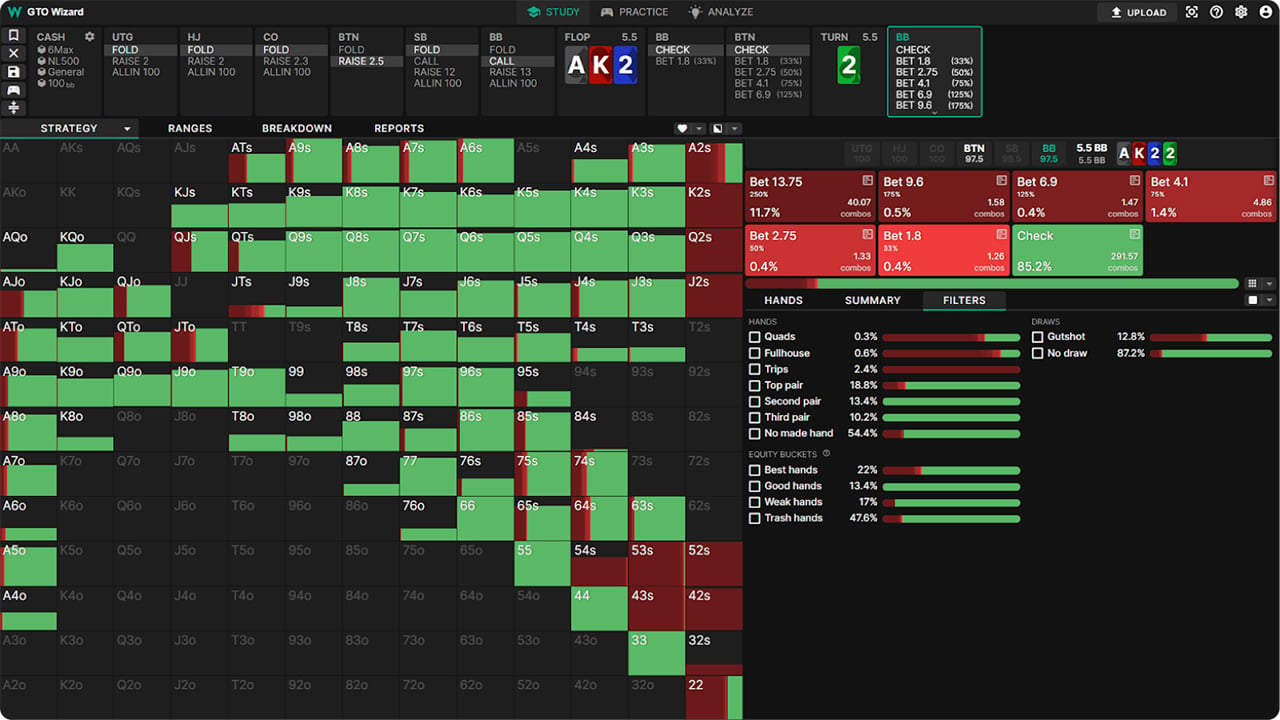
Example 1: BB Probe vs IP SRP

Here we see a BB vs BTN probe strategy on AK22r after the flop checks through. The pot is 5.5BB, the stack is 97.5BB, and there are two streets left. The geometric size here is 252% pot. As you can see, the GTO strategy here is to bet geometrically or not at all.

BB has a nut advantage in trips, so they press that advantage as hard as possible to get stacks in by the river.

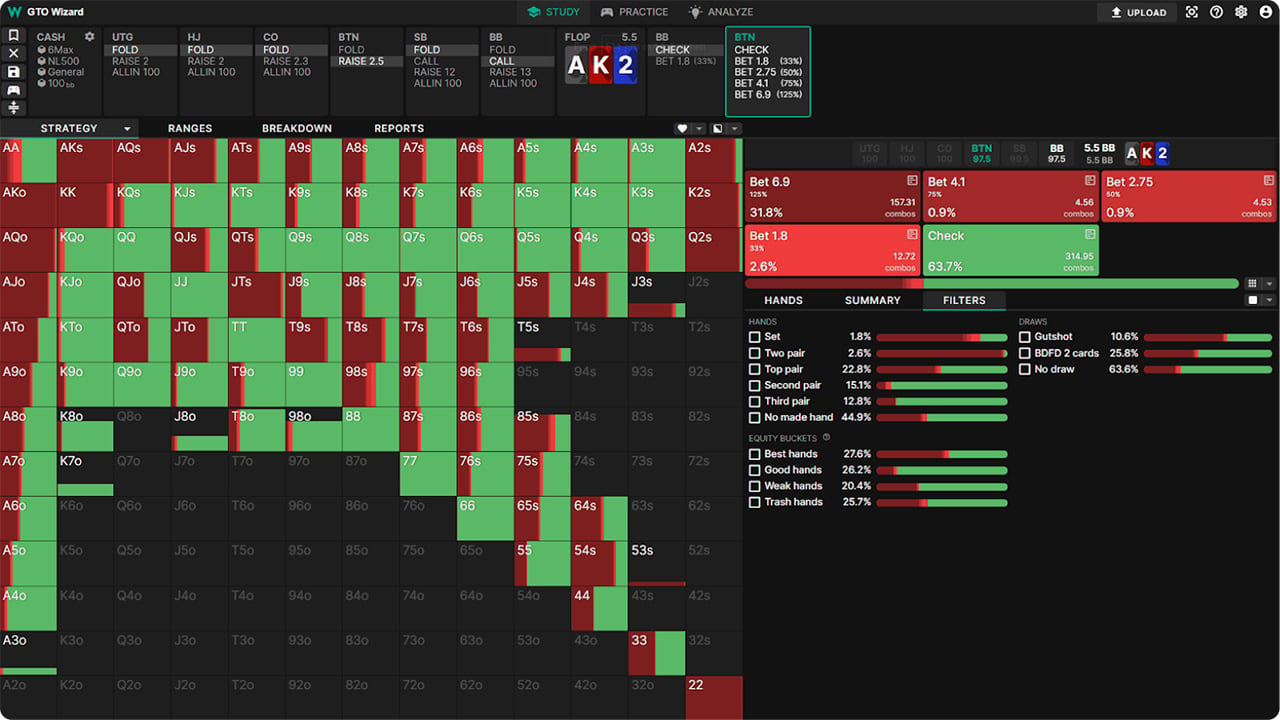
Example 2: IP C-Bet vs BB

We see a similar strategy on the flop in position. Here BTN has a major top pair advantage and presses it using the geometric bet size over three streets:

Non-Geometric Strategies

Let’s examine our goals and assumptions.

These goals and assumptions are not necessarily true. The geometric betting strategy is designed for perfectly polarized situations, but that’s rarely the case in practice.

A perfectly polarized range only consists of the invulnerable nuts and pure bluffs (relative to villain’s range). Equity is static (nothing can improve or get worse). But actual poker is full of draws and equity is not static. Most hands can improve or get worse by the river.

More importantly, you rarely have enough nutted hands to implement this strategy. Most medium hands cannot play for stacks without overplaying their value.

GTO strategies are non-geometric in the majority of spots. GTO rarely uses a geometric strategy before the turn, as ranges are too close and equity too dynamic. Equities crystalize on later streets and ranges become more polar, incentivizing geometric bet sizes. When equities run much closer and can shift more easily on early streets, this is not the case.

Conclusion