How To Adjust When Villain Has No Bluffs

“They always have it!” is a common, semi-joking expression in poker to describe the tendency of a certain type of player to never bluff. It is used whenever a seemingly passive player makes an out of character, aggressive play.

Thanks to the new Nodelocking feature, we can see what a solver would do when a player indeed “always has it” when they are aggressive. I’ve actually studied this in depth because a book project I have just completed is all about nodelocking. The writing process would’ve been much easier if GTO Wizard’s nodelocking feature had been available at the time. Nevertheless, it’s exciting to dive into the mind of the AI.

GTO vs. the Never Bluffer

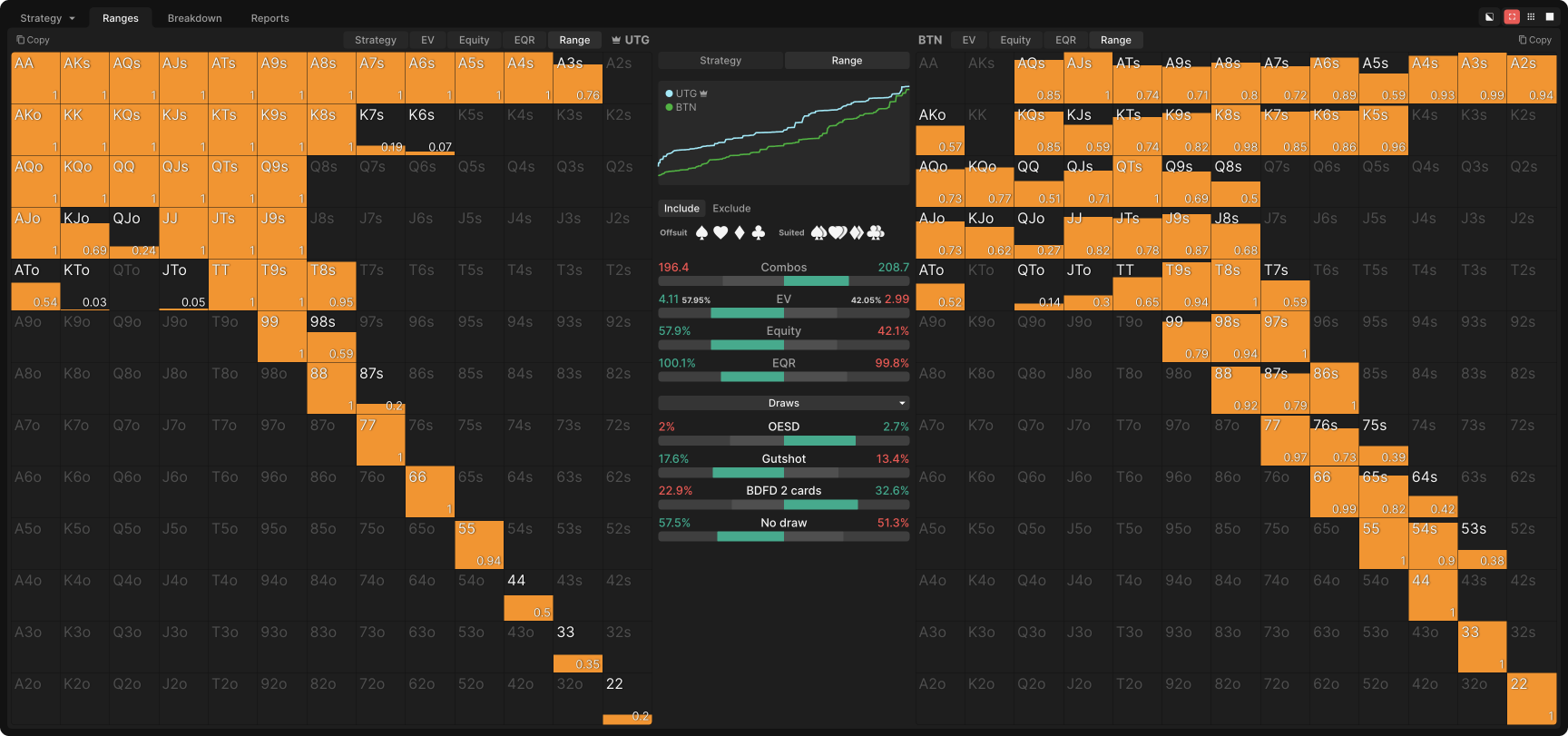
In this example, we have used the preflop ranges for 60bb effective, UTG vs BTN, single-raised pot from the solutions library. We then fed that into the AI configured to use the Automatic bet sizing option (the best option if you are new to this specific feature or nodelocking in general).

The flop is K♥J♦2♣.

These are the preflop ranges:

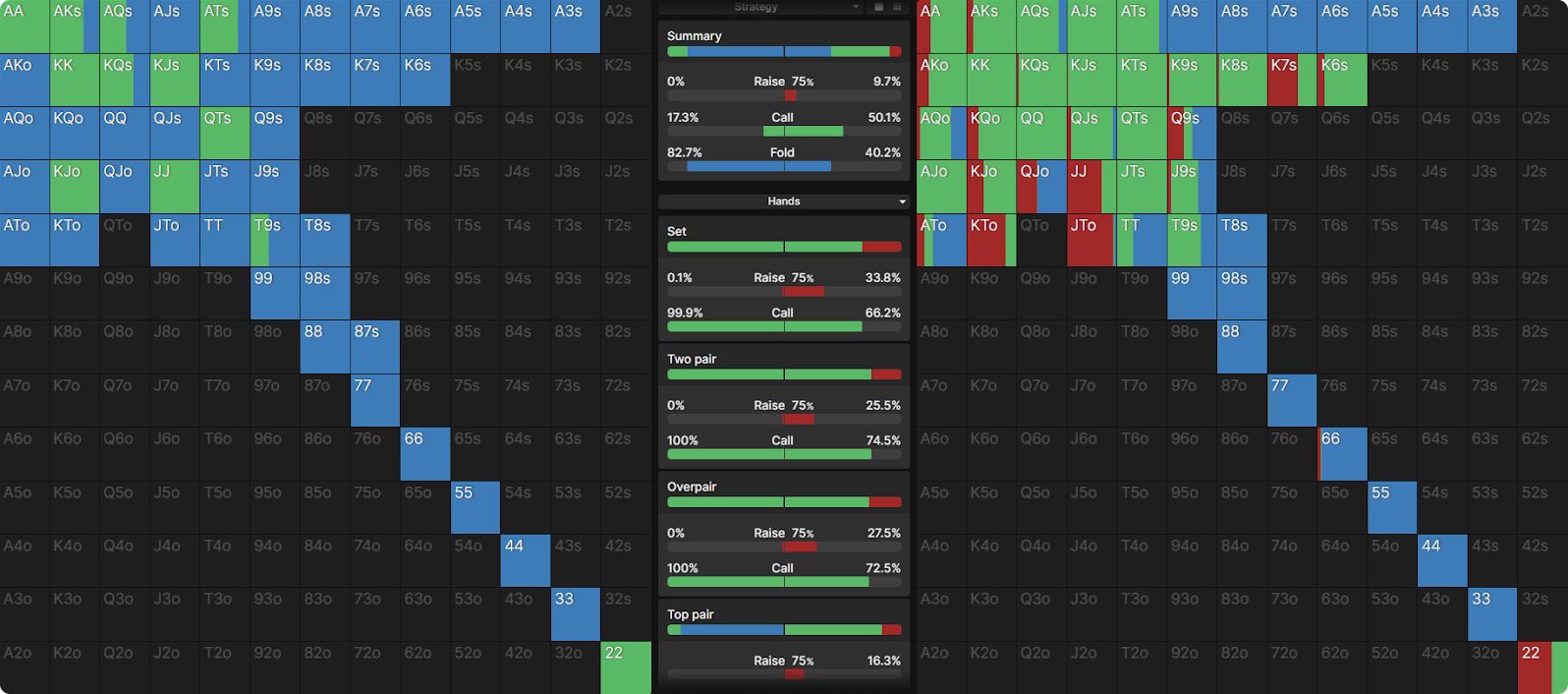
In this example, UTG bets 67% of the time for 39% pot (we will look at their betting range in a moment). When they do bet, BTN responds as shown below:

There is a raising range of 10% of hands, using a 56% pot size. The value hands are mostly top pair or better. The bluffs are mostly semi-bluff hands like QTs for an open-ended straight draw or hands like T♦9♦ for a gutshot with a backdoor flush draw. There are also hands like A♦5♦, which have both a backdoor flush and backdoor wheel straight draw to go along with their overcard. I would also include the times that hands like 44 and 33 bet as bluffs because although they are made hands that can get called by worse (in the form of draws), they are never happy about being called.

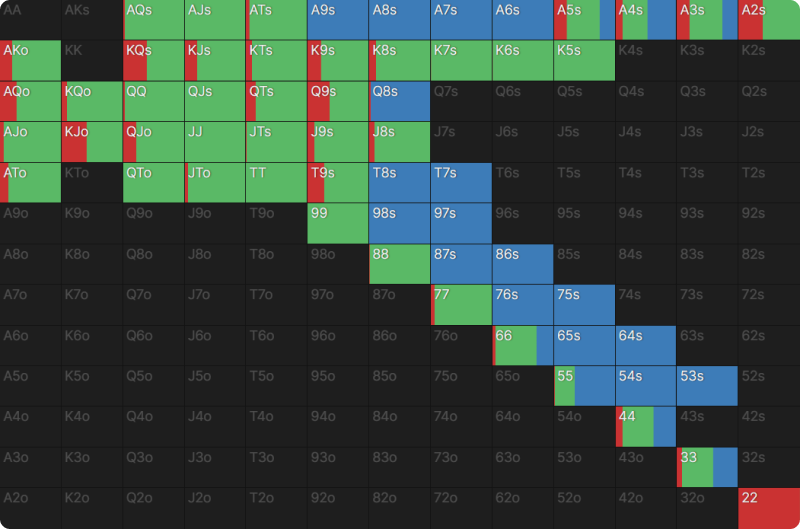
But what if we felt our opponent never bluff raises in spots like this? They might bluff when UTG checks to them but would never raise a continuation bet from UTG.

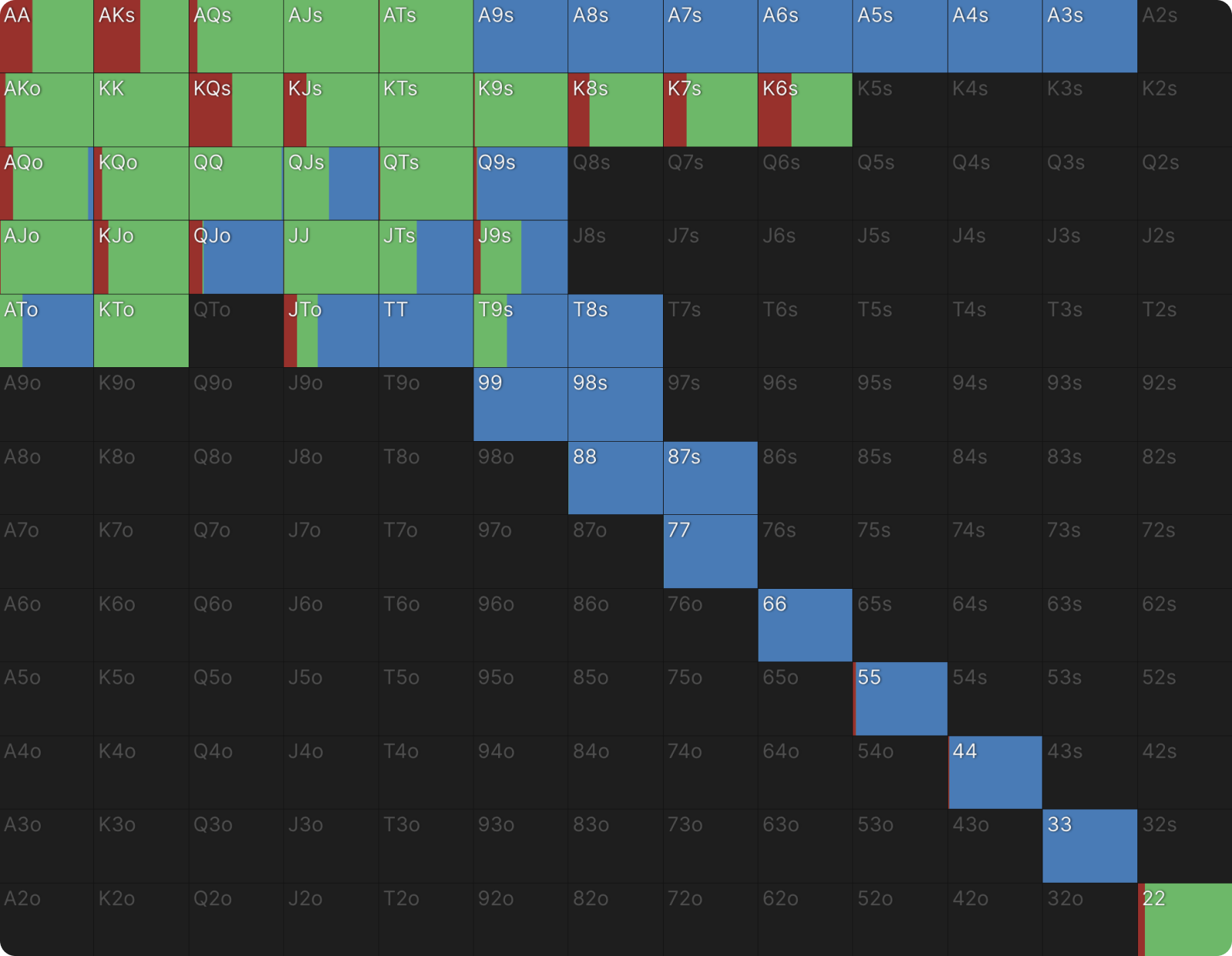
Using the nodelocking feature, we change the BTN’s response to this:

We have an almost identical percentage of continues. However, all the hands we categorized as bluffs have become calls instead. In practice, if we don’t think our opponent bluffs, we might also reasonably assume they don’t bluff catch with small pocket pairs or Ace-high, nor may they raise a hand like J9s which is just second pair, weak kicker, weak (backdoor straight) draw. You can experiment with such a player type yourself in GTO Wizard, but to make as close a comparison as possible, let’s go with the same value range but no bluffs.

The adjustments the solver makes highlight several reliable heuristics I have discovered that apply over and over again against players who do not bluff.

Be More Aggressive

One of the most curious things about nodelocking is that sometimes the adjustment to a player’s leak happens on an earlier branch of the game tree, not the one where the leak occurs. This is common when a player does not have any bluffs.

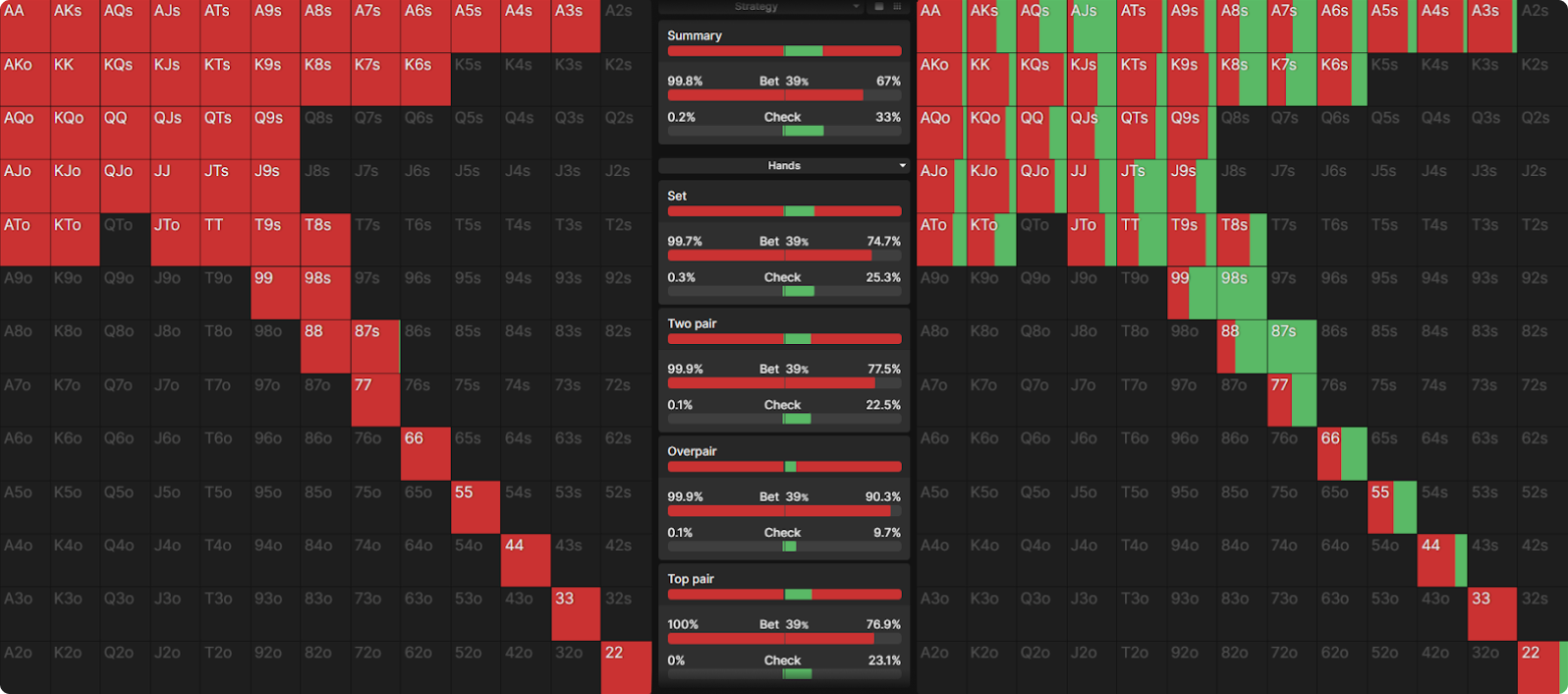
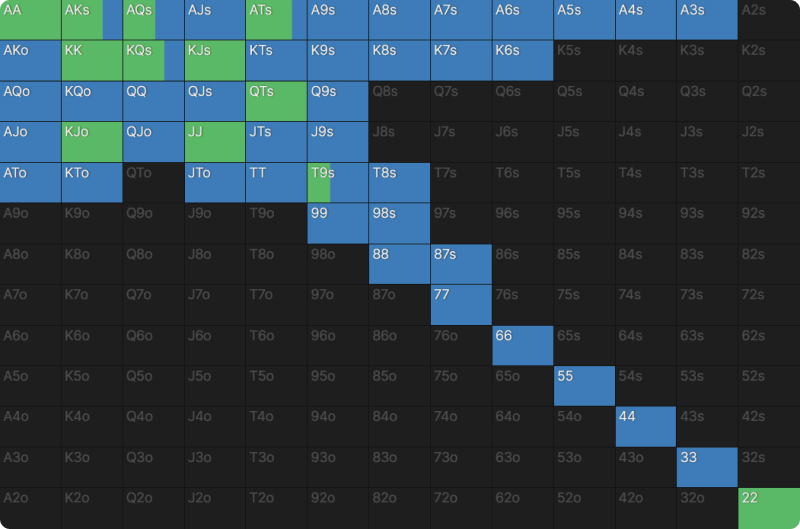
If we go back to the start of the flop, we can see the first big adjustment using the ‘Compare Nodes’ feature. This is what UTG does at the start of the hand:

In the GTO solution, UTG has range advantage but is out of position, so they didn’t go for a range-bet, instead opting to bet 67% of the time. When BTN never bluffs, UTG gets to drive up the betting frequency from 67% to 100% of the time.

Solvers hate getting raised and having to fold away equity. Solvers would bet at a much higher frequency were it not for the fact that they would get raised more often.

It might seem counterintuitive to lead more frequently when an opponent’s raising range is that much stronger in our no-bluff example, but we are not trying to induce a raise; we are targeting the rest of the BTN’s range that calls or folds. Playing against a player who doesn’t bluff is much easier in that respect. They are more passive with the rest of their range, and when they do raise, we can be very confident we are usually beat, and get away cheaply.

You might also discover if you experiment with Dynamic or Fixed bet sizes that the solver will also have a bigger preference to size bets larger for a similar reason.

Fold More to Their Aggression

The first adjustment may have surprised you, but the next one will not. This is the adjustment most thinking players have always made against players with no bluffing range, even before the solver era. It stands to reason that if your opponent never bluffs, they have a very strong range, and as a result, you also need a stronger-than-usual range to continue.

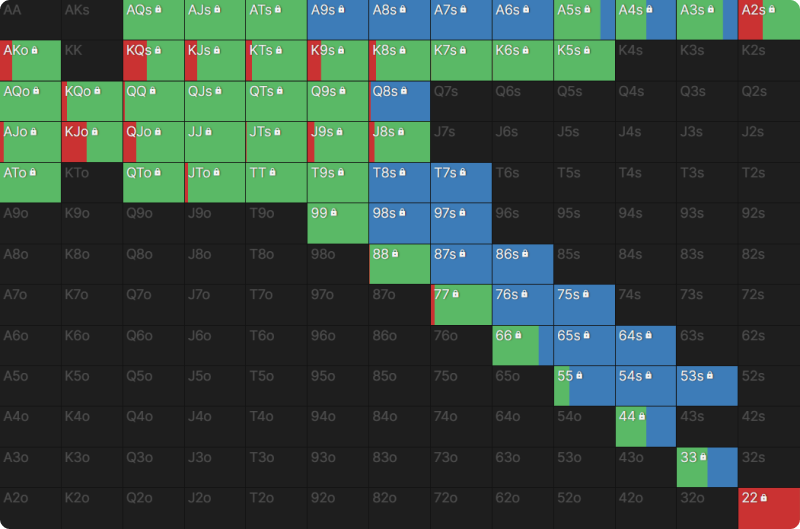
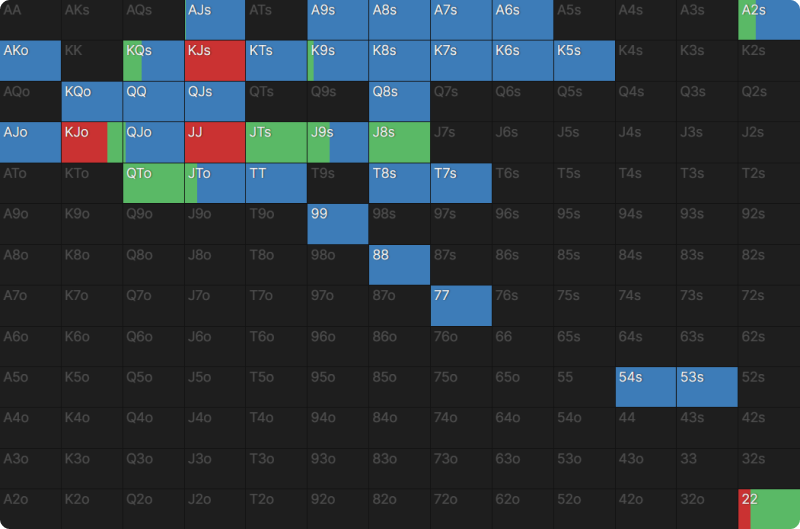
Facing the raise from the BTN, this is the Compare Nodes view for our nodelocked and unlocked GTO solutions for UTG:

In the GTO solution (right), we fold 40% of the time. But in this nodelocked version (left), we fold 82% of the time. Our hands, which we would categorize as ‘bluff catchers,’ become useless against players who do not bluff.

Therefore, we fold twice as many hands compared to the GTO example. We fold very strong hands like KTs and QQ here because they can rarely be good against a range that starts at 2nd pair.

Improvability Becomes More Important

We fold very strong made hands because our opponent never bluffs, but we still continue with a few unmade hands that can jump ahead of a lot of the opponent’s hands. As you can see below, we sometimes call AQs, ATs, QTs, and T9s.

Why do we call with QTs but fold QQ? Because hands like this can outdraw a very strong value range and win a lot of chips when they do. The second benefit mentioned refers to the concept of implied odds. All these hands can make straights, and in the case of ATs and AQs, they can also make a better top pair. Except for QTs, these suited hands fold when they are Spades because they don’t have a backdoor flush draw on this spadeless rainbow board.

Raise Less Often (or Not at All)

You will have noticed that the GTO solution, when facing the BTN raise, had a 3-betting range, which included bluffs like ATo, Q9s, and 66. And on the value side, hands like 22, JJ, AA, AKo, KJo, and KTo. This is the GTO response:

There is no such 3-betting range in the nodelocked solution; we call our best hands and fold the rest.

We know our opponent has a value-heavy range and will likely to continue to bet further streets, so we let them do it when we have a strong hand. When we have a draw like QTs, we don’t want to bet because we will never get folds (i.e., we have no fold equity) and our hand wants to see the next card as cheaply as possible.

One important consideration with nodelocking is that once you have changed part of the game tree, the solver will play as close to perfectly as possible on all the other nodes before and afterward. Therefore, if we did an additional nodelock to strengthen UTG’s 3-betting range to top pair top kicker or better, the BTN would fold some very strong hands. This is how the BTN would respond:

3-betting here would simply fold out hands like AK and KQ which we want to see calls from.

In practice, if you suspect your never bluffing opponent is also never folding, you might be better off getting it in with your big hands before a turn card comes that might scare/slow them down. But here, we just call because there is a high certainty that we will get further bets from them on the turn and river.

This is another recurring lesson from nodelocking: if your opponent makes some sort of error, let them keep making it.

It’s much better to let them keep firing with a very transparent range than to give them an opportunity to fold when they otherwise would have paid you off over several streets. Solvers will typically keep the opponent in the part of the game tree where they are making mistakes rather than force them out of it.

Conclusion

A common denominator between all these adjustments is that when your opponent has no bluffs, they are unbalanced. In response, you get to be unbalanced too. You get to bet more often, knowing they are less likely to bluff you, but you fold all your bluff catchers when they do take an aggressive action. You no longer need bluffs to balance your value hands and can simply play the best hands in your range.