Theoretical Breakthroughs in ICM

Today, we’ll share one of the most significant theoretical breakthroughs in tournament poker since the invention of the Independent Chip Model (ICM). We’ve developed a powerful new technique that allows tournament players to solve ICM spots in a fraction of the time required by traditional methods while being orders of magnitude more accurate. By integrating this new technique with GTO Wizard AI, MTT players can now solve postflop ICM spots in seconds, even when thousands of players remain!

ICM: A Quick Recap

In poker tournaments, the value of chips is not constant. Unlike cash games where chips have a fixed value, in tournaments, your chips serve only as a means of survival to try and place as deep in the money as possible. This creates a misalignment between two goals: accumulating chips (Chip EV Strategies) and winning prizes (ICM Strategies). This is why the Independent Chip Model (ICM) was created.

The Independent Chip Model is a mathematical formula that takes players’ stacks as input and outputs the likelihood of each stack placing in each position. These placement probabilities, along with the prize structure, are used to calculate the monetary value of each stack and can be used to optimize tournament decisions. This article explains how the basic ICM formula works.

Postflop ICM & Chip EV Benchmarks

It’s first worth asking, how misaligned are these goals of accumulating chips vs winning prizes? In a previous article, we benchmarked Chip EV vs ICM strategies in a series of preflop push/fold tournaments and found that ICM strategies significantly outperformed Chip EV. However, these experiments only tested preflop. Now that we have postflop ICM solving, the natural first step was to benchmark postflop Chip EV against ICM players.

It is quite alarming to see that on the bubble and at the final table, playing Chip EV loses upwards of 10% of your initial buy-in on every single flop! In 3-bet pots, playing Chip EV can lose upwards of 30% of your buy-in on average. Note that we only nodelocked the flop strategies, meaning Nemesis assumed perfect play on future streets. Losses would be even worse if we measured turns and rivers as well. Even with 25% of players remaining (15% paid), we see non-negligible losses. This demonstrates that playing ICM-aware strategies is crucial to your tournament success.

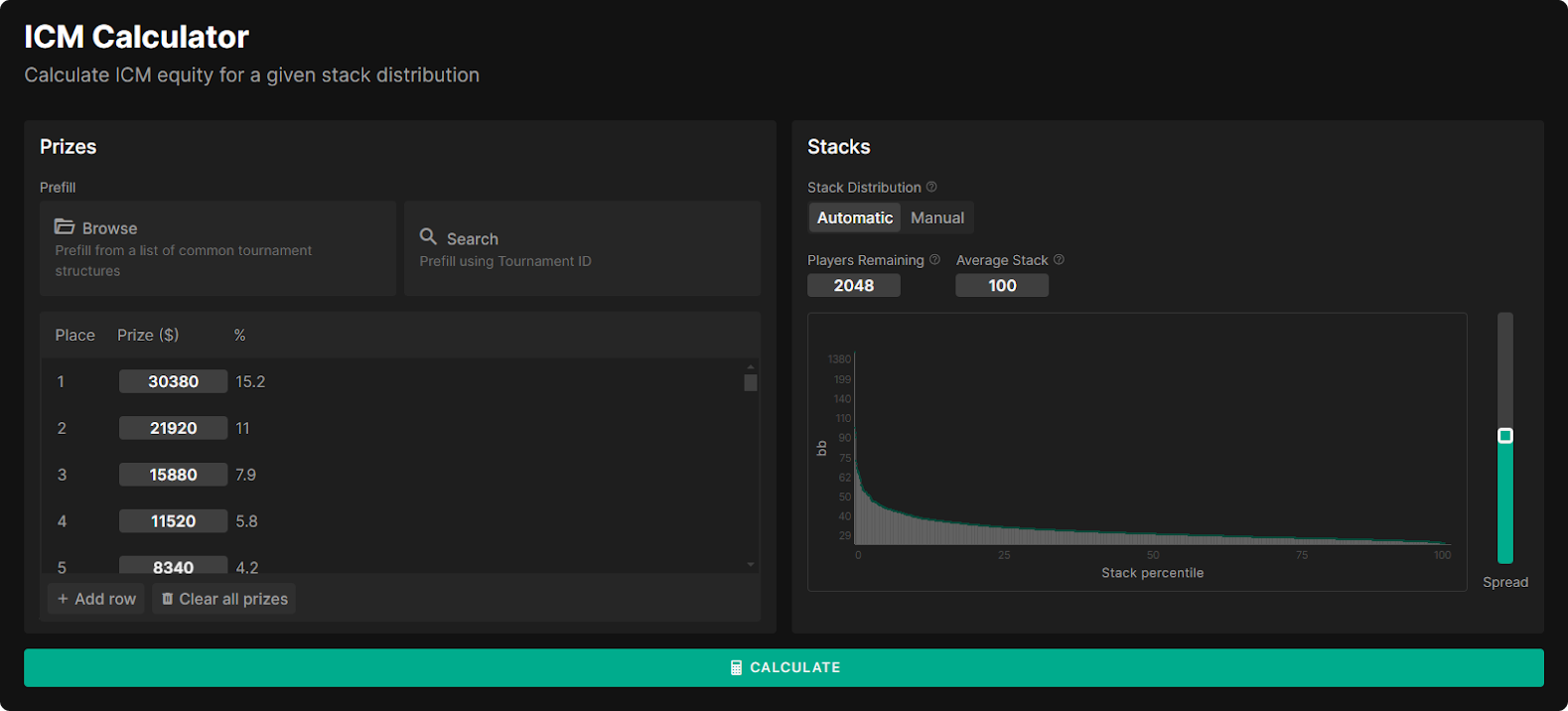
Free ICM Calculator

We’ve created a free public utility that can calculate the ICM value of up to 2048 players’ stacks! Type in any set of prizes and stacks, and calculate the tournament equity and $EV of each stack according to the Independent Chip Model!

Our ICM calculator, as well as our GTO Solver, feature many useful tools to save time:

GTO Wizard ICM – Our Method

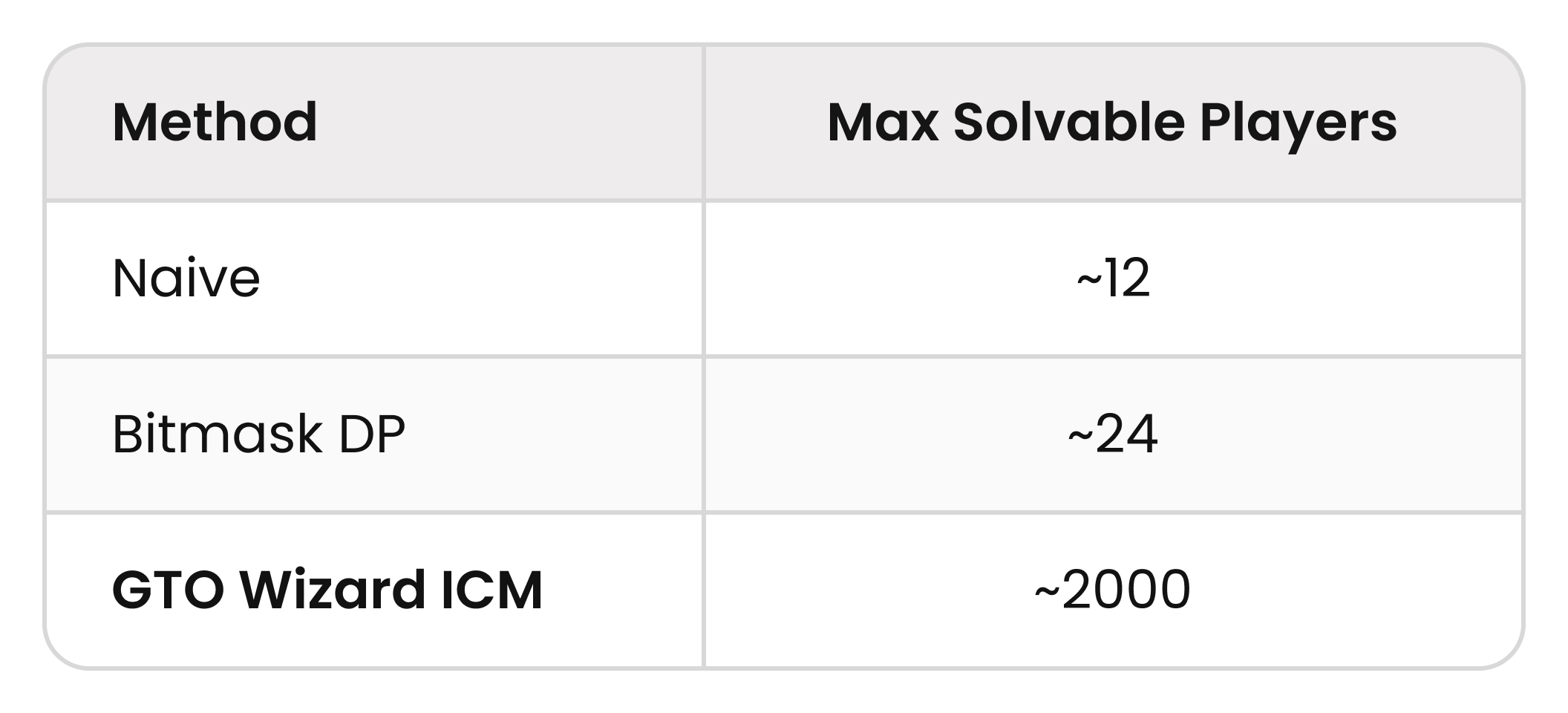
Our new algorithm makes it possible to compute ICM values while achieving both high accuracy and efficiency, but this was previously thought to be impossible. The main challenge was the computational difficulty: exact computation (of ICM) requires accounting for all possible player rankings, but enumerating these rankings quickly becomes intractable as the number of players increases.

To support tournaments with 30 or more players, we needed to find a way to consider these rankings without explicitly listing them. The simplest approach would be to use a sampling method: some possible rankings are sampled probabilistically, and the ICM values are estimated based on these samples. However, while this method allows you to handle a large number of players, the results are only estimates, and the accuracy was not satisfactory to us.

Inspired by the theoretical aspects of the sampling method, we devised a new method that is significantly more accurate while remaining highly efficient. Our achievement is a purely algorithmic advancement, meaning that it does not rely on any abstractions, interpolations or machine-learning techniques. It relies purely on the theoretical math that underpins the ICM calculation. Our method gives precise ICM values. This makes it inherently versatile and robust, and capable of handling any sort of input!

We cannot give away our exact methodology. However, we have benchmarked performance against traditional ICM calculation methods to demonstrate its speed and efficiency.

Comparing ICM Calculation Methods

Over the years, numerous attempts have been made to improve the speed and efficacy of ICM calculations. In this article, we compare several prominent methods with our own.

ICM Calculation Methods

The Setup

Firstly, we needed a way to calculate the exact ICM values for our setup, one that doesn’t rely on our own models or inferences. We found a special case that can be computed exactly based on the paper On a Model for Storage and Search published in 1973. This specific case involves stacks increasing linearly while prizes decrease linearly:

For the development of our own ICM algorithm, we conducted extensive testing with a variety of special cases (like the one above) where the ground truth values could be determined using specific algorithms tailored to each case. The worst relative error we found did not exceed 3e-9 (0.0000003%), and we confirmed that more than 12 digits typically match. Again, our algorithm is universal and does not exploit any special structure of each test case, while the logic implemented for testing does.

Results

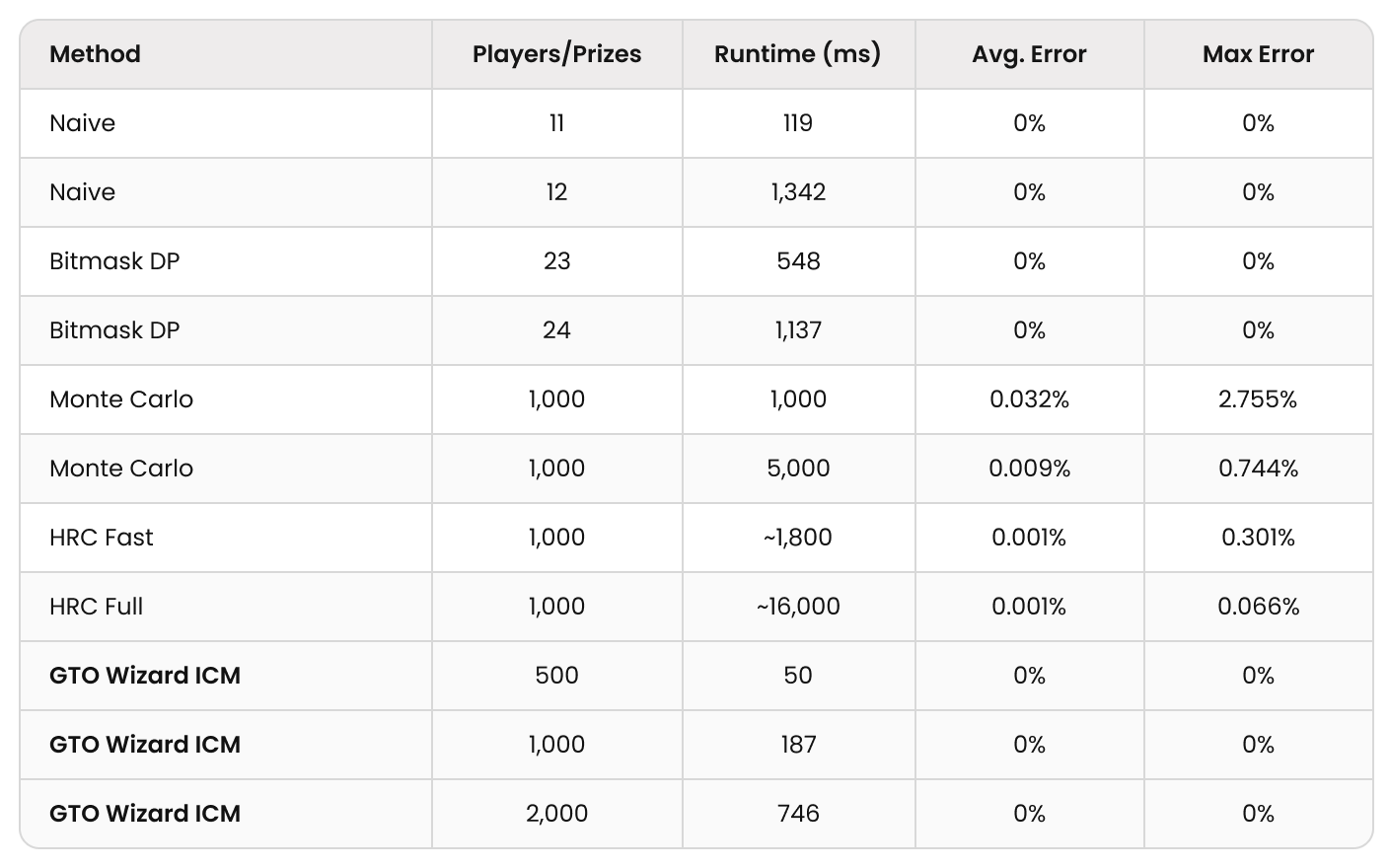
Here we compare exact ICM methods. The following table displays the maximum computable number of players in one second using a single CPU thread (Ryzen 7950x):

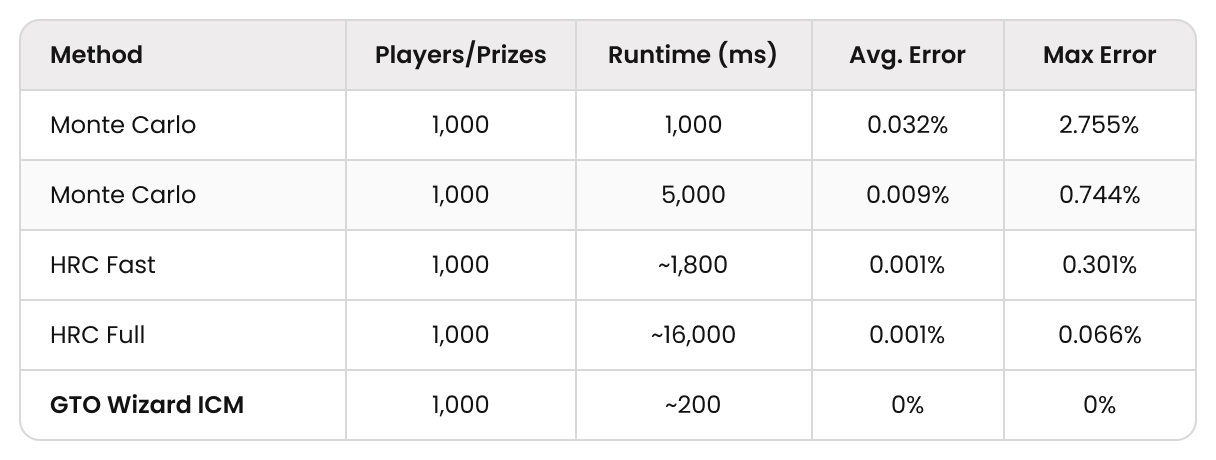
Next, we compared our algorithm against two approximate algorithms; Monte Carlo and HRC:

GTO Wizard ICM is orders of magnitude more accurate than other approximate methods while requiring only a fraction of the computational time.

Modeling Bounties

Many modern day poker tournaments use bounties – a prize that’s won for eliminating another player. Creating a new state-of-the-art ICM computational model wasn’t enough. We needed a way to estimate the bounty equity in tournaments, including the likelihood of winning a bounty this hand and future hands.

Since this was no small task, we break down our full methodology in this article:

Bounty Models Explained: Solving Knockout Tournaments

Summary & Acknowledgements

Solving optimal MTT strategies is no small task. The non-linear nature of chip utility means that the value of your stack depends on every stack in the tournament. To solve this problem, we had to address a wide variety of engineering challenges:

The end result is the world’s most powerful tool for finding optimal tournament strategies!

I would like to give a special shoutout to two of our engineers: Philippe Beardsell, our lead engine developer, and Wataru Inariba, who cracked the new ICM formula, for their hard work. They ran these benchmarks and guided this article. We’d also like to give special thanks to Adam Kelly for coming up with CSTE and assisting us with this project. At GTO Wizard, we’re proud to employ the best minds in the industry to push the frontiers of poker theory.